Законы трения

Как трение, так и сцепление являются следствием шероховатости поверхности и сервовитной пленки, возникающей в зоне контакта.

Чтобы снизить трение необходимо уменьшить взаимодействие тел в зоне контакта на молекулярном уровне. Для снижения коэффициента трения используют смазки, а также подбираются материалы с низким коэффициентом трения.

Сервовитная пленка — защитная металлическая пленка, в которой протекает диффузионно-вакансионный механизм сдвига. Возникает в начальной стадии трения в результате избирательного растворения анодных компонентов поверхностного слоя металла или сплава.

Законы трения:

1)  сила трения направлена противоположно скорости и параллельно плоскости;

2)  модуль силы трения равен произведению реакции опоры на коэффициент трения;

3)  сила трения постоянна, а сила сцепления возрастает от 0 до максимального значения, пока тело не придет в движение;

4)  сила трения не зависит от удельной поверхности трущихся тел.

При качении реакция опоры смещается, так как происходит продавливание.

При действии сдвигающей силы, приложенной к катку, покоящемуся на шероховатой поверхности, возникает сила, противодействующая возможному смещению тела из равновесного положения или его действительному перемещению при его движении и пара сил, момент которой препятствует повороту катка. Возникновение пары сил, препятствующей качению, связана с деформацией опорной плоскости, в результате которой равнодействующая нормальных реактивных сил по площадке контакта смещена от линии действия силы тяжести в сторону возможного или действительного движения.

Область равновесия

С помощью понятия конуса трения можно определить область возможных равновесных положений.

Для этого достаточно по заданным коэффициентам трения определить углы трения, определяющие предельные положения полной реакции и построить конусы трения. Общая область конусов дает область равновесных положений.

Так как сила P не пересекает заштрихованную область, то равновесия не будет.

Трение верчения

Пример решения задачи на силы трения и сцепления

1)  Прикладываем все силы.

2)  Разделяем конструкцию на части.

3)  Применяем принцип освобождаемости от связей.

Левая часть

Правая часть

Центр параллельных сил в пространстве.

Центр тяжести. Свойства параллельных сил.

Определение центра тяжести плоской фигуры, объема, линии

Центром тяжести твердого тела называется центр параллельных сил тяжести частиц, слагающих тело. Иными словами, центр тяжести – это такая точка приложения равнодействующей сил тяжести частиц тела, которая остаётся неизменной при любых поворотах тела.

Таким образом, для определения положения центра тяжести можно использовать формулы для координат центра параллельных сил.

Тело состоит из n элементарных объемов. Найдем равновесие такой системы сил, приложенных в некоторой точке C.

Обозначим силы веса отдельных частиц тела 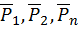, координаты его центра тяжести 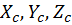, координаты любой частицы твердого тела и 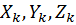, а вес будет равен

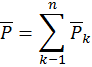
Тогда формулы для определения координат центра тяжести принимают вид:

; ;

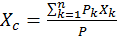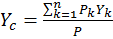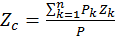
Определим положение центра тяжести однородных тел. Точка С – центр сил в пространстве с координатами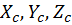

Свойства параллельных сил и равнодействующей:

1)  Если силы повернуть в любом направлении на любой угол, то равнодействующая повернется на тот же угол и будет проходить через тоску С.

2)  Если предположить, что P1 и P2 вес элементарных объемов, то равнодействующая будет являться весом, а точка С будет центром масс.

Координаты можно найти по теореме Вариньона:

; ;

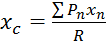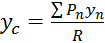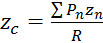
3)  Если в качестве P1 и Pn представить элементарно малую фигуру, то

; ;

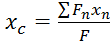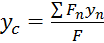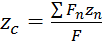
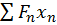— статический момент площади фигуры

4)  Если в качестве P1 и Pn представить элементарно малый объем, то

; ;

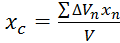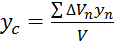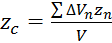
5)  Если в качестве P1 и Pn представить элементарно малую длину, то

; ;

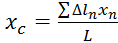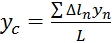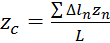
Примеры:

Метод отрицательных площадей

Метод отрицательных площадей –сложная фигура разбивается на совокупность простых фигур, для которых известны положения центра тяжести или легко определяются, но при наличии отверстий или пустот удобно их представление в виде “отрицательных” областей.

1) 

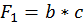
2) 

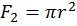
3) 

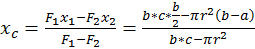
4) 

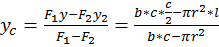
Графический метод

Найдем координаты X графическим методом.

Найдем центры каждой части конструкции.

Выбираем полюс с таким расчетом, чтобы прямые О и 4, проведенные от крайних точек вертикали к полюсу, образовали при пересечении между собой прямой угол.

Затем полюс Р соединяем линиями – лучами со всеми точками, соответствующими площадям, и при помощи треугольников переносим эти линии строго параллельно — под схему, привязывая каждую к соответствующему перпендикуляру того: первый луч О — к перпендикуляру из центра С1; второй 1 — к С2 и т, д.

Экспериментальный метод

Центры тяжести неоднородных тел сложной конфигурации можно определять экспериментально: методом подвешивания и взвешивания. Первый способ состоит в том, что тело подвешивается на тросе за различные точки. Направление троса, на котором подвешено тело, будет давать направление силы тяжести. Точка пересечения этих направлений определяет центр тяжести тела.

Метод взвешивания состоит в том, что сначала определяется вес тела, например самолета. Затем на весах определяется давление самолета на опору. Составив уравнение равновесия относительно какой — либо точки, можно вычислить расстояние от этой оси до центра тяжести.

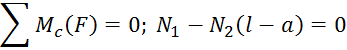
Другой вариант

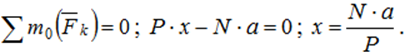
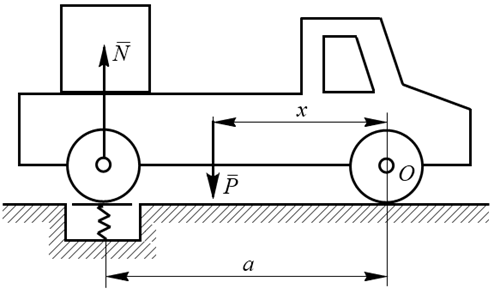
Список литературы

1. Бутенин Н. В., Лунц Я. Л., Меркин Д. Р. Курс теоретической механики. Т. 1 «Статика. Кинематика», Т.2 «Динамика».ЛАНЬ, – СПб., 2008.–729 с.

2. Добронравов В. В., Никитин Н. Н., Дворников А. Л. Курс теоретической механики. – М., ВШ, 2009. – 719 с.

3. Тарг С. М. Краткий курс теоретической механики. – М., ВШ, 2008, – 416 с.

4. Никитин Н. Н. Курс теоретической механики. — М.: ВШ,2010.-719 с.

5. Яблонский А. А., Никифорова В. М. Курс теоретической механики. – М. И НТЕГРА-ПРЕСС, 2009. – 603 с.

6. Мещерский И. В. Сборник задач по теоретической механике. – М., 2008, –448 с.

7. Яблонский А. А. Сборник заданий для курсовых работ по теоретической механике. – М. ,ВШ, 2009. –307 с.

В разработке электронной версии курса лекций по теоретической механике «статика» принимали участие студенты группы 13 – М – СЖ1:

Грешнов А. А., Горшков И. И.