Амплитуда отраженной волны
Поскольку масса электронов много меньше массы ионов плазмы, постольку скорость колеблющихся электронов много больше скорости ионов, значит, переменный ток плазмы в подавляющей своей части — ток электронов. Задача данного раздела состоит в исследовании переизлученной колеблющимися электронами электромагнитной волны.
2.2 Амплитуда отраженной волны
Рассмотрим плазменный слой толщиной b, перпендикулярно которому падает электромагнитная волна с напряженностью электрического поля E. Пусть ne — число электронов в единице объема плазменного слоя.
Под действием электрического поля все электроны совершают согласованное движение, создавая электронный ток. Чтобы определить параметры отраженной волны, найдем плотность тока, создаваемого движущимися электронами. Она равна j=-enev, где v — скорость электронов. Значение v найдем, решив уравнение движения электрона. Оно имеет вид
mea=-eE(t), (1)
где E(t)=Eosinwt, Eo — амплитуда напряженности электрического поля волны, w — частота волны. Из механики известно, что если ускорение колеблющейся частицы a(t)=aosinwt, то закон движения частицы описывается формулой — x(t)=—![]() sinwt. В нашем случае амплитуда ускорения равна ao=
sinwt. В нашем случае амплитуда ускорения равна ao=![]() , где e и me — заряд и масса электрона. Так что x(t)=
, где e и me — заряд и масса электрона. Так что x(t)=![]() sinwt. Соответственно скорость v(t)=wx0coswt, или
sinwt. Соответственно скорость v(t)=wx0coswt, или
v(t)=![]() coswt. (2)
coswt. (2)
Плотность тока, таким образом, равна
j(t)=ev(t)ne=j(t)= ![]() necoswt. (3)
necoswt. (3)
Линейная плотность тока, приходящаяся на всю толщину слоя, равна j(t)b. Ток слоя в примыкающих к нему точках создает магнитное поле индукции
B(t)= mo j(t)b= mob ![]() ne coswt. (4)
ne coswt. (4)
Электрическое поле в этих же точках, как было показано на предыдущем занятии, имеет напряженность
E(t)=c×B(t)= cmob ![]() necoswt. (5)
necoswt. (5)
Амплитуда отраженной волны равна ![]()
![]() neb. Она тем больше, чем толще плазменный слой и чем больше электронная плотность в плазме. Это справедливо до тех пор, пока амплитуда отраженной волны гораздо меньше амплитуды падающей. При больших значениях произведения neb надо учитывать, что электроны движутся в результирующем поле, являющемся суммой полей падающей волны и переизлученной самими же электронами. Реальная зависимость амплитуды напряженности электрического поля отраженной волны имеет вид, изображенный на рисунке 20. Начальный участок является линейным. При больших neb асимптотически зависимость приближается к значению амплитуды падающей волны, и фаза оказывается сдвинутой не на
neb. Она тем больше, чем толще плазменный слой и чем больше электронная плотность в плазме. Это справедливо до тех пор, пока амплитуда отраженной волны гораздо меньше амплитуды падающей. При больших значениях произведения neb надо учитывать, что электроны движутся в результирующем поле, являющемся суммой полей падающей волны и переизлученной самими же электронами. Реальная зависимость амплитуды напряженности электрического поля отраженной волны имеет вид, изображенный на рисунке 20. Начальный участок является линейным. При больших neb асимптотически зависимость приближается к значению амплитуды падающей волны, и фаза оказывается сдвинутой не на ![]() , а на p. При этом падающая электромагнитная волна полностью отражается от толстого плазменного слоя.
, а на p. При этом падающая электромагнитная волна полностью отражается от толстого плазменного слоя.
Ионосфера Земли имеет такую толщину, что короткие радиоволны отражаются от нее. Наличие ионосферы позволяет осуществлять дальнюю радиосвязь: посланные передающей станцией радиоволны многократно отражаясь от ионосферы и от поверхности Земли могут достигнуть антенны принимающей станции, расположенной далеко за горизонтом.
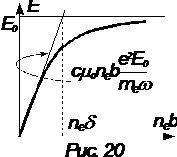 В металлах электронная плотность значительно превышает электронную плотность ионосферы Земли, поэтому даже пластинка микронной толщины может обеспечивать полное отражение электромагнитной волны.
В металлах электронная плотность значительно превышает электронную плотность ионосферы Земли, поэтому даже пластинка микронной толщины может обеспечивать полное отражение электромагнитной волны.
3. Давление электромагнитной волны
3.1 Отражение от поверхности металла
Вопрос 1. Какова, на ваш взгляд, причина того, что от металлической пластинки отражается практически вся падающая волна?
Вопрос 2. Часть падающей на металл электромагнитной волны поглощается. Почему это происходит?
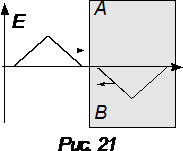 Задача 1[C12.1.19]. При больших значениях плотности электронов проводимости в единице объема металла составляющая напряженности электрического поля волны, параллельная поверхности металла, ослабляется практически до нуля. Поэтому решение задачи о электромагнитной волне вблизи поверхности металла сводится к отысканию таких бегущих волн, наложение которых дает нулевую составляющую напряженности электрического поля вдоль поверхности. При перпендикулярном падении на металлическую поверхность две волны: одна реально движется в пространстве вне металла, а другая, фиктивная, “перевернутая” волна движется навстречу первой внутри металла (на рисунке 21 эта область вместе с фиктивной волной находится справа плоскости AB). Фиктивная волна становится реальной, как только она выходит за границу AB, где она налагается на падающую волну. Наложение этих волн слева от плоскости AB дает нулевую напряженность электрического поля вдоль AB и, следовательно, решает поставленную задачу. Используя описанный прием, найдите распределение напряженности электрического поля и индукцию магнитного поля вблизи металлической плоскости в момент, когда вершина падающей волны достигает плоскости AB.
Задача 1[C12.1.19]. При больших значениях плотности электронов проводимости в единице объема металла составляющая напряженности электрического поля волны, параллельная поверхности металла, ослабляется практически до нуля. Поэтому решение задачи о электромагнитной волне вблизи поверхности металла сводится к отысканию таких бегущих волн, наложение которых дает нулевую составляющую напряженности электрического поля вдоль поверхности. При перпендикулярном падении на металлическую поверхность две волны: одна реально движется в пространстве вне металла, а другая, фиктивная, “перевернутая” волна движется навстречу первой внутри металла (на рисунке 21 эта область вместе с фиктивной волной находится справа плоскости AB). Фиктивная волна становится реальной, как только она выходит за границу AB, где она налагается на падающую волну. Наложение этих волн слева от плоскости AB дает нулевую напряженность электрического поля вдоль AB и, следовательно, решает поставленную задачу. Используя описанный прием, найдите распределение напряженности электрического поля и индукцию магнитного поля вблизи металлической плоскости в момент, когда вершина падающей волны достигает плоскости AB.
Задача 2. На зеркальную металлическую подложку нанесен толстый эмульсионный слой. При нормальном падении электромагнитной волны большой частоты — света — на расстоянии 10-5мм от металлической поверхности произошло почернение эмульсии. Объясните этот эффект. Определите длину волны света, падающего на металлическую поверхность. На каком расстоянии от поверхности подложки оказался второй почерневший слой?
3.2 Механизм давления на металлическую поверхность
Падающая и отражающаяся от металлической поверхности электромагнитная волна создает давление. Физическая причина давления состоит в том, что под действием электрического поля свободные заряды совершают колебания. Эти колебания совершаются в магнитном поле электромагнитной волны, так что заряды испытывают силу Лоренца. Сила Лоренца действует в направлении распространения волны, создавая давление.
Используя результаты анализа п. 2.2 — уравнения (1) — (3), убедитесь, что сила Лоренца, действующая на свободные носители заряда, ориентирована в направлении распространения падающей электромагнитной волны.
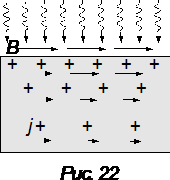 Рассмотрим сопровождающий рисунок. Поскольку электромагнитная волна проникает вглубь металла только на некоторую глубину, следует ожидать, что плотность тока неоднородно распределена вблизи поверхности — убывает по мере погружения внутрь металла. Пусть в некоторый момент времени ток (на рисунке показан направленным от наблюдателя оперением стрелок — крестиками) распределен так, как показано на рисунке 22. Направление магнитного поля, создаваемого током в металле, определим по правилу буравчика: вблизи поверхности — слева направо; в глубине — справа налево (эта область на рисунке не показана). Сила Лоренца, действующая на приповерхностный ток, направлена вглубь металла, т. е. в направлении падающей волны.
Рассмотрим сопровождающий рисунок. Поскольку электромагнитная волна проникает вглубь металла только на некоторую глубину, следует ожидать, что плотность тока неоднородно распределена вблизи поверхности — убывает по мере погружения внутрь металла. Пусть в некоторый момент времени ток (на рисунке показан направленным от наблюдателя оперением стрелок — крестиками) распределен так, как показано на рисунке 22. Направление магнитного поля, создаваемого током в металле, определим по правилу буравчика: вблизи поверхности — слева направо; в глубине — справа налево (эта область на рисунке не показана). Сила Лоренца, действующая на приповерхностный ток, направлена вглубь металла, т. е. в направлении падающей волны.
Проведем качественное рассмотрение давления электромагнитной волны на поверхность металла при заданных значениях напряженности электрического поля. При оценке давления необходимо определить силы Лоренца, действующие на все участвующие в движении свободные носители заряда. Для этого необходимо знать магнитную индукцию взаимодействующей с поверхностью металла волны и плотность тока. Значение магнитной индукции определяется по напряженности электрического поля результирующей волны с использованием идеи решения задачи 1. Плотность тока, как выше отмечалось, можно оценить по значению магнитного поля в результирующей волне вблизи поверхности металла.
Задача 3 [C12.1.22]. На металлическую стенку падает перпендикулярно ее поверхности синусоидальная плоская электромагнитная волна. Амплитуда напряженности электрического поля волны равна Eo. Определите поверхностную плотность тока в стенке и среднее давление волны на нее.
Решение. Магнитная индукция равна
B=E/c. (6)
Ток, возбуждаемый электромагнитной волной, сосредоточен в тонком приповерхностном слое. Проводя оценку, будем считать, что ток распределен по поверхности с линейной плотностью jлин=jd, где d —толщина токового слоя, j — средняя по объему плотность тока. Выберем прямоугольный контур, частично погруженный в металл, с площадкой, перпендикулярной поверхности и вектору плотности тока. Здесь следует иметь в виду, что внутри металла (на глубине) поле равно нулю, зато снаружи оно двойное. В соответствии с теоремой о циркуляции, примененной к этому контуру, имеем
2B=m o jлин. (7)
Отсюда, а также из уравнения (6) находим
jлин=![]() =2eocE. (8)
=2eocE. (8)


