Изучение дифракции когерентного излучения в параллельных лучах
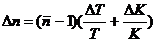 . (15)
. (15)
11. Записать окончательный результат и сделать вывод.
Контрольные вопросы.
1. Каков физический смысл показателя преломления?
2. Как связан показатель преломления диэлектрика с его диэлектрической проницаемостью, диэлектрической восприимчивостью, поляризуемостью молекул?
3. Как зависит показатель преломления воздуха от давления?
4. Как устроен интерферометр Майкельсона? Как получают в нем когерентные лучи?
5. Что называется оптической разностью хода лучей?
6. Как изменяют оптическую разность хода лучей в данной работе?
7. Как меняется наблюдаемая интерференционная картина при изменении оптической разности хода?
8. Назовите виды интерферометров и области их использования.
ЛАБОРАТОРНАЯ РАБОТА 3
Изучение дифракции когерентного излучения в параллельных лучах
Цель работы: изучение явления дифракции, определение диаметра отверстия, ширины щели, периода дифракционной решетки, определение длины волны лазерного излучения.
Оборудование: лазер, диафрагма, набор объектов для исследования (экран с круглым отверстием, экран со щелью, дифракционные решетки), поворотное зеркало, полупрозрачный экран.
Описание метода измерения
Дифракцией называется совокупность явлений, наблюдаемых при распространении света и в среде с резкими неоднородностями. Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. При прохождении света через преграды каждый элемент волнового фронта можно считать источником вторичных волн. Распределение интенсивности за преградой определяется интерференцией вторичных волн, проходящих в данную точку от всех элементов волновой поверхности, с учетом их амплитуды и фаз (принцип Гюйгенса-Френеля). Наблюдение дифракции осуществляется с помощью экрана, расположенного за преградой.
Различают дифракцию в параллельных лучах (дифракция Фраунгофера) и дифракцию в расходящихся лучах (дифракция Френеля). В этой работе рассматривается дифракция Фраунгофера.
1. Дифракция на длинной узкой щели. Пусть параллельный монохроматический пучок света падает на щель шириной h (рис. 1). Тогда на экране за щелью будет наблюдаться дифракционная картина в виде чередующихся темных и светлых полос. С помощью построения, показанного на рис. 1, можно определить угол, под которым будет наблюдаться максимум интерференционной картины. В соответствии с принципом Гюйгенса Френеля можно рассматривать щель как систему вторичных источников (зон Френеля) S1. Если в направлении под углом ![]() разность хода от соседних источников составляет
разность хода от соседних источников составляет ![]() , то волны от этих источников, собранные линзой в одной точке экрана, гасят друг друга т. к. приходят в эту точку в противофазе. В случае четного числа источников, укладывающихся на ширине щели, в точке экрана, расположенной под углом
, то волны от этих источников, собранные линзой в одной точке экрана, гасят друг друга т. к. приходят в эту точку в противофазе. В случае четного числа источников, укладывающихся на ширине щели, в точке экрана, расположенной под углом ![]() к первоначальному направлению распространения света будет наблюдаться минимум. Если же число источников нечетное, то остается один не скомпенсированный источник, и в этом случае под углом
к первоначальному направлению распространения света будет наблюдаться минимум. Если же число источников нечетное, то остается один не скомпенсированный источник, и в этом случае под углом ![]() будет наблюдаться максимум. Оптическая разность хода лучей, идущих от крайних зон, равна
будет наблюдаться максимум. Оптическая разность хода лучей, идущих от крайних зон, равна ![]() h sin
h sin![]() . Таким образом, условие минимума имеет вид
. Таким образом, условие минимума имеет вид
h sin![]() =
=![]() ,
,![]() (1)
(1)
условие максимума освещенности h sin![]() =
=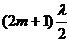 ,
,![]()
где ![]() — длина волны света, m=0, ±1, ±2, ±3,… — порядки дифракционных минимумов. Очевидно, что по угловому расстоянию между дифракционными минимумами можно определить длину световой волны, если известна ширина щели, и наоборот.
— длина волны света, m=0, ±1, ±2, ±3,… — порядки дифракционных минимумов. Очевидно, что по угловому расстоянию между дифракционными минимумами можно определить длину световой волны, если известна ширина щели, и наоборот.
2. Дифракция на круглом отверстии. Согласно принципу Гюйгенса Френеля, для получения результирующей амплитуды под заданным углом ![]() , необходимо просуммировать волны, излученные всеми участками этой круговой апертуры. Вклад каждого элемента отверстия в приближении Фраунгофера составляет cos(kr)*dA, где k=2
, необходимо просуммировать волны, излученные всеми участками этой круговой апертуры. Вклад каждого элемента отверстия в приближении Фраунгофера составляет cos(kr)*dA, где k=2![]() — волновое число, r – радиус-вектор (рис. 2), dA – элемент площади внутри апертуры. Амплитуда световой волны в точке, находящейся под углом
— волновое число, r – радиус-вектор (рис. 2), dA – элемент площади внутри апертуры. Амплитуда световой волны в точке, находящейся под углом ![]() к первоначальному направлению распространения, определяется интегралом
к первоначальному направлению распространения, определяется интегралом
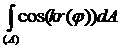 , (2)
, (2)
который не берется в элементарных функциях. Его решением является функция Бесселя первого рода J1(x). График этой функции представлен на рис. 3.
Первый минимум дифракционной картины соответствует условию J1(x)=0. В нашем случае x= . Таким образом, условие первого минимума дифракции на круглом отверстии приобретает вид
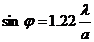 . (3)
. (3)


Аналогично можно получить условия минимумов и максимумов более высоких порядков. Положения нескольких первых максимумов и минимумов можно выразить приближенным условием
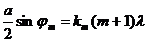 , (4)
, (4)
где m = 1,2,3,…, а – диаметр отверстия. Значения km для минимумов и максимумов приведены в таблице. Дифракционная картина представляет собой чередование светлых и темных колец. Сужение отверстия приводит к расплыванию дифракционной картины. При увеличении а дифракционная картина стягивается в точку.
|
m |
kmax |
kmin |
|
0 |
0 |
0.61 |
|
1 |
0.41 |
0.56 |
|
2 |
0.44 |
0.54 |
|
3 |
0.46 |
0.53 |
3. Дифракционная решетка. Систему большого числа близких параллельных щелей называют дифракционной решеткой. Расстояние d=a+b (a – ширина щели, b – ширина промежутка между щелями) называется постоянной, или периодом, дифракционной решетки (рис. 4). Главные дифракционные максимумы возникают в тех направлениях, для которых оптическая разность хода лучей, идущих от соседних щелей решетки, равна целому числу длин волн ![]()
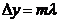 . (5)
. (5)
Из рис. 4 видно, что оптическая разность хода лучей Dy, идущих от двух соседних щелей под углом дифракции j, определяется выражением
![]()
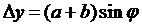 . (6)
. (6)


