Релятивистский импульс. релятивистская масса
Рассмотрим теперь это же столкновение в системе отсчета, в которой v1x=0. Определим изменяющуюся проекцию скорости в новой системе отсчета, скорость которой . Для первой частицы 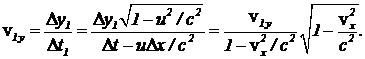 (1) Соответственно изменение скорости первой частицы равно
(1) Соответственно изменение скорости первой частицы равно 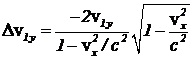 . (2) Для второй частицы
. (2) Для второй частицы 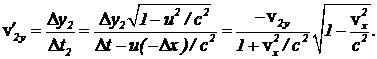 (3) Изменение скорости второй частицы равно
(3) Изменение скорости второй частицы равно 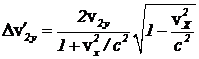 . (4)
. (4)
Поскольку v1Y=v2Y, постольку видно, что изменение скорости второй частицы оказывается меньшим, чем изменение скорости первой частицы. Если теперь в качестве определения импульса возьмем классическое определение, то получится, что импульс сохраняется в ц-системе, но не сохраняется в новой системе отсчета, движущейся относительно ц-системы.
2.3 Релятивистский импульс. Релятивистская масса
Если бы при определении импульса массу частицы умножали не на скорость в выбранной системе отсчета, а на отношение перемещения к промежутку собственного времени, за которое произошло перемещение, то выражение импульса выглядело бы так:
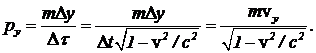 (5)
(5)
При таком определении последовательность выкладок (1) — (4) привела бы к сохранению импульса. Кроме того, очевидно, что при v<<c данное определение дает классическую формулу: p=mv.
Каждая из проекций должна определяться, как py: 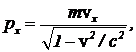 (6)
(6)
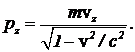 (7)
(7)
или в векторной форме 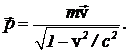 (8)
(8)
Замечательно, что можно оставить прежнее определение импульса (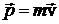 ), если под массой частицы понимать величину
), если под массой частицы понимать величину
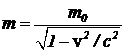 , (9)
, (9)
где m0 — масса покоящейся частицы. Ее называют инвариантной массой. Почему — будет видно позднее. Массу частицы, определяемую формулой (9), называют релятивистской массой. Она тем больше, чем ближе скорость частицы к скорости света.
2.4 Решение задач
Задача 1. Постройте приблизительный график зависимости ![]() .
.
Задача 2. Во сколько раз релятивистская масса электрона больше массы покоя при скорости электрона 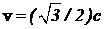 ?
?
Задача 3. При какой скорости релятивистская масса частицы больше массы покоя в 100 раз?
2.5 Релятивистское уравнение движения частицы
Чтобы уравнения движения частиц удовлетворяли принципу относительности, второй закон Ньютона надо подправить. Оказывается, второй закон Ньютона, записанный через импульс, не противоречит принципу относительности, если в него подставлять релятивистский импульс. Релятивистское уравнение движения имеет вид: 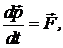 (10)
(10)
где импульс определяется уравнением (8).
Задача 4. Рассмотрите движения заряженной частицы с массой покоя m0, c зарядом q, ускоряемой однородным электрическим полем. Пусть напряженность ![]() направлена вдоль оси OX, и частица движется вдоль OX. Пусть в начальный момент времени частица покоилась.
направлена вдоль оси OX, и частица движется вдоль OX. Пусть в начальный момент времени частица покоилась.
а) Найдите зависимость импульса частицы от времени.
б) Используя выражение релятивистского импульса через скорость, найдите зависимость скорости от времени.
в) При каких условиях результат решения приближенно описывается классической формулой?
г) Получите асимптотическое значение скорости при t® ![]() . Как отличается результат от классического решения?
. Как отличается результат от классического решения?
д) Начертите приблизительный график зависимости v(t).
Решение. а) Движение одномерное, поэтому уравнение движения принимает вид 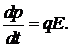 (11)
(11)
Уравнение (11) можно переписать для приращений
dp=qEdt. (12)
Так как величина qE постоянна, суммирование по конечному промежутку времени от 0 до t дает
p(t)-p(0)=qEt. (13)
Если частица начинает движение из состояния покоя, тогда p(0)=0 и уравнение (13) можно переписать в виде
p(t)=qEt. (14)
б) Выразим импульс через скорость, тогда 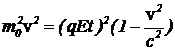 или
или 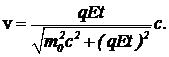 (15)
(15)
в) При ![]() вторым слагаемым под радикалом в правой части уравнения можно пренебречь, тогда выражение скорости принимает вид
вторым слагаемым под радикалом в правой части уравнения можно пренебречь, тогда выражение скорости принимает вид 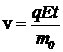 . (16)
. (16)
Этот результат совпадает с результатом классического решения задачи. Обратим внимание на то, что классическая формула получается как приближенный результат в предельном случае.
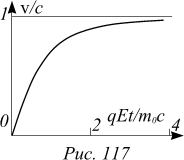 г) При
г) При ![]() первым слагаемым под радикалом в правой части уравнения можно пренебречь, тогда v®c в соответствии с постулатом теории относительности.
первым слагаемым под радикалом в правой части уравнения можно пренебречь, тогда v®c в соответствии с постулатом теории относительности.
д) В этой части решения задачи полезно возвратиться к материалу занятия 1.5.1, где обсуждались результаты опытов по ускорению электрическим полем заряженных частиц.
Результаты решения задачи 4 согласуются с экспериментальными данными опытов по ускорению заряженных частиц электрическим полем.
3. Домашнее задание
3.1 Теоретический материал
Проработать материал занятия по пособию и своим конспектам. Дополнительно по учебнику “Физика 11” под ред. А. А.Пинского. §54. Стр.228-229 (Релятивистский импульс и масса).
3.2 Решение задач
Задача 1. При какой скорости релятивистская масса электрона будет равна массе покоя протона?
Задача 2. Заряженная частица инвариантной массы m0 c зарядом q со скоростью v влетела в однородное магнитное поле с индукцией B. С какой угловой скоростью движется частица? Чему равен радиус кривизны траектории частицы? На основе полученного результата предложите экспериментальный способ измерения импульса частиц.
Задача 3. Родившаяся частица инвариантной массы m0 оставила в пузырьковой камере, помещенной в однородное магнитное поле индукции B, след в виде дуги окружности радиуса R длиной L. Чему равно собственное время жизни частицы, если ее заряд равен e?
занятие 1.6.2
энергия. инвариантная масса
2. Релятивистская энергия
2.1 Кинетическая энергия частицы
После работ Лоренца, Эйнштейна, Пуанкаре, заложивших основу теории относительности, физикам стало ясно, что любой физический закон, любое уравнение, выражающее этот закон, должны быть инвариантны относительно преобразований Лоренца. Так уравнение движения частицы инвариантно относительно преобразований Лоренца, если оно записано через импульс. При этом оно выглядит точно так же, как второй закон Ньютона. Итак, релятивистское уравнение движения частицы имеет вид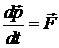 . (1) Пусть частица движется в силовом поле
. (1) Пусть частица движется в силовом поле ![]() , которое зависит только от координат частицы. Пусть
, которое зависит только от координат частицы. Пусть ![]() — бесконечно малое перемещение частицы под действием силы
— бесконечно малое перемещение частицы под действием силы ![]() . Умножим обе части уравнения (1) на это перемещение:
. Умножим обе части уравнения (1) на это перемещение: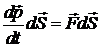 . (2)
. (2)
Правая часть уравнения равна работе силы ![]() при данном перемещении частицы. Если просуммировать обе части уравнения (2) по всем участкам траектории между двумя заданными точками 1 и 2, то в правой части получится полная работа силы A12, совершаемая при перемещении между этими точками. Если в начальном состоянии p=0, то левая часть после суммирования представляется в виде
при данном перемещении частицы. Если просуммировать обе части уравнения (2) по всем участкам траектории между двумя заданными точками 1 и 2, то в правой части получится полная работа силы A12, совершаемая при перемещении между этими точками. Если в начальном состоянии p=0, то левая часть после суммирования представляется в виде
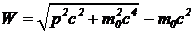 , (3)
, (3)
так что из уравнения движения следует 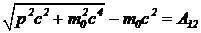 . (4)
. (4)


