Колебания в распределённых системах
|
|
(8.58) |
что согласуется с оценкой (7.30), если положить w2 = wн + w1.
Тема 9. Колебания в распределённых системах.
Колебательный процесс в системе с сосредоточенными параметрами, в которой потенциальная и кинетическая энергии запасаются в различных элементах, описывается обыкновенными ДУ. В системах же с распределёнными параметрами любой, сколь угодно малый, элемент запасает как кинетическую, так и потенциальную энергию. Примеры — маятник и струна, LC-контур и волновод. Колебания в таких системах описываются ДУ в частных производных.
Система может считаться системой с сосредоточенными параметрами, если её геометрические размеры много меньше длины волны колебания. Если же они сравнимы, то это — система с распределёнными параметрами, в которой условие квазистационарности принципиально не выполняется. Если размеры системы много больше длины волны, то для анализа процессов используется волновая трактовка Даламбера (полное движение представляет собой сумму бегущих в обе стороны волн). В рамках же данного курса нас будут интересовать системы, размеры которых порядка длины волны и к которым применима колебательная трактовка Бернулли, рассматривающая любой процесс как сумму собственных колебаний системы (стоячих волн).
9.1. Телеграфные уравнения, волновое уравнение
|
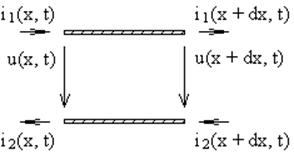
Рассмотрим распределенную колебательную систему на примере двухпроводной линии. Если расстояние между проводниками мало в сравнении с длиной линии l и длиной волны l, передаваемых колебаний в ней, то векторы магнитного и электрического поля лежат в плоскости, перпендикулярной направлению линии, в этой плоскости удовлетворяют уравнению Лапласа и могут считаться потенциальными. Поэтому для малых участков |
Рис. 79. Двухпроводная линия. |
линии dx (рис. 79) можно ввести понятия потенциала, тока, распределенных ёмкостей и индуктивностей. Если система не излучает и не взаимодействует с другими проводниками, то в каждом сечении линии токи в обоих проводниках равны по величине и противоположны по направлению: i1(x, t) = —i2(x, t) = i(x, t).
Рассмотрим бесконечно малый элемент dx длины линии, обладающей индуктивностью L и ёмкостью C на единицу длины линии. Для участка dx линии можно записать уравнения Кирхгофа:
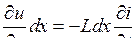 ,
, 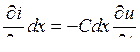 ,
,
откуда легко получаются телеграфные уравнения:
|
|
(9.1) |
Из уравнений (9.1) легко получаются и волновые уравнения для тока и напряжения:
|
|
(9.2) |
где
|
|
(9.3) |
Волновое уравнение можно получить также, если рассматривать, например, распределённую электрическую систему как предельный случай одномерной цепочки, составленной из сосредоточенных индуктивностей и емкостей. Если увеличивать число ячеек на единицу длины цепочки, сохраняя постоянной общую индуктивность и ёмкость, то в пределе система уравнений для цепочки (8.32) перейдёт в волновое уравнение (9.2). Координата x соответствует изменяющемуся номеру ячейки.
Частным решением волнового уравнения (9.2) являются любые функции вида
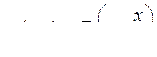 ,
, 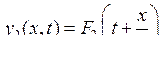 ,
,
соответственно полное решение имеет вид:
|
|
(9.4) |
Первое слагаемое описывает волну, которая распространяется, не меняя своей формы, в направлении возрастания x, а второе — волну, распространяющуюся с той же скоростью в сторону убывания x. Для процессов, синусоидальных во времени, решение (9.4) принимает форму
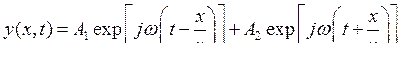 .
.
Здесь величина w(t ± x/v) называется фазой волны, а величина k = w/v — волновым числом. Волновое число характеризует пространственную периодичность волнового процесса, т. е. y(x + nl, t) = y(x, t), и связана с длиной волны соотношением: k = 2p/l.
Для токов и напряжений в линии решение уравнения (9.4) имеет вид:
|
|
(9.5) |
Подставляя эти выражения в телеграфное уравнение (9.1), получим связь между коэффициентами:
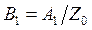 ,
, 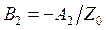 ,
,
где ![]() — волновое сопротивление линии. Учитывая связь между коэффициентами, перепишем (9.5) в виде
— волновое сопротивление линии. Учитывая связь между коэффициентами, перепишем (9.5) в виде
|
|
(9.6) |
Погонные индуктивность и ёмкость линии определяются её геометрией. Для двухпроводной линии в системе СГС получаем
|
|
(9.7) |
где r — радиус проводов, b — расстояние между ними.
Учитывая два последних соотношения, получим для волнового сопротивления следующее выражение:
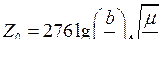 [Ом].
[Ом].
Для коаксиальной линии имеем
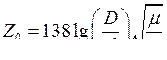 [Ом],
[Ом],
где D и d — диаметры внешнего и внутреннего проводников.
Подставляя погонные L и C в (9.3), получим, что фазовая скорость волны в линии равна
|
|
(9.8) |
Для двухпроводной линии с погонным сопротивлением проводников R и погонной утечкой G между ними телеграфные уравнения (9.1) принимают вид:
 ,
,
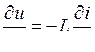 ,
, 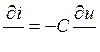 .
.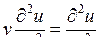 ,
, 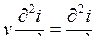 ,
,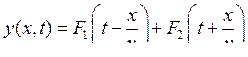 .
.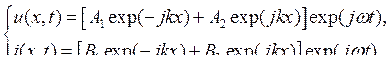
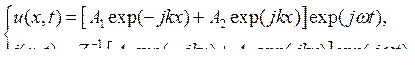
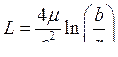 ,
, 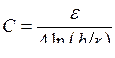 ,
,

