Динамика механизма вращения поворотной части крана при разгоне и торможении
Ограничимся рассмотрением малых колебании груза, когда ![]() , при неизменной длине подвеса груза. С учётом этого допущения
, при неизменной длине подвеса груза. С учётом этого допущения 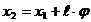 , усилие в подвеске груза
, усилие в подвеске груза 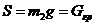 и горизонтальная проекция натяжения в подвеске
и горизонтальная проекция натяжения в подвеске
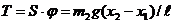
Уравнение движения тележки
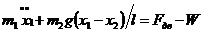 (5.1)
(5.1)
Уравнение движения груза в горизонтальном направлении имеет вид
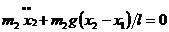 (5.2)
(5.2)
Рассмотрим приведенную динамическую систему по схеме на рис. 5.1, б, когда масса m2 скользит по опорной поверхности без трения. Движение этой системы описывается уравнением
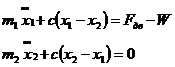 (5.3)
(5.3)
Сравнивая систему уравнений (5.3) с системой уравнении (5.1) и (5.2), замечаем, что они идентичны, если принять за ![]() величину
величину 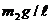 . Отсюда следует, что динамическое действие колеблющегося груза на тележку ( или кран) аналогично прикреплению к тележке массы
. Отсюда следует, что динамическое действие колеблющегося груза на тележку ( или кран) аналогично прикреплению к тележке массы ![]() груза при помощи пружины с жесткостью
груза при помощи пружины с жесткостью ![]() . Эта аналогия позволяет наглядно оценить влияние раскачивающегося груза:
. Эта аналогия позволяет наглядно оценить влияние раскачивающегося груза:
При ![]() отклоняющийся груз «помогает» движущей силе
отклоняющийся груз «помогает» движущей силе ![]() , а при
, а при ![]() он увеличивает силы сопротивления передвижению тележки.
он увеличивает силы сопротивления передвижению тележки.
Основная литература [3, с. 349…351]
Дополнительная литература [10, с. 164…167]
Контрольные вопросы:
1. Назовите причины необходимости учёта раскачивания груза при уточнённых расчётах грузоподъёмных машин.
2. Каким образом (вместе или раздельно) можно рассчитывать маятниковые колебания груза по сравнению с упругими колебаниями крана?
3. Приведите аналогию динамического воздействия колеблющегося груза на тележку (или кран), позволяющую наглядно оценить влияние раскачивающегося груза.
Лекция 6
Динамика механизма вращения поворотной части крана при разгоне и торможении
При неустановившемся вращении поворотной части крана возникают инерционные сопротивления, обусловленные инерцией его поворотной части вместе со стреловым рабочим оборудованием и инерцией груза. Эти сопротивления можно определить по уравнению:
![]() , (6.1)
, (6.1)
где mг – масса груза; lО – расстояние от центра груза до оси вращения поворотной части; JО – момент инерции поворотной части крана относительно его оси вращения; ω0 и ωд – угловые скорости поворотной части крана и ротора двигателя; u – передаточное число механизма; tР – время разгона механизма вращения.
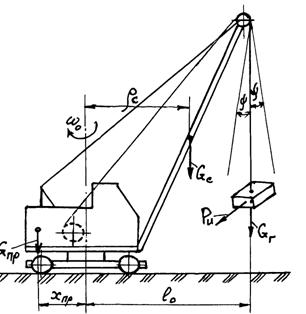
Рисунок 6.1 — Схема стрелового крана к расчету механизма вращения
Применительно к схеме машины, изображенной на рис. 6.1:
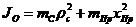 ,
,
где mС и mПр – массы стрелы и противовеса; ρс и xПр – плечи действия сил тяжести этих масс относительно оси вращения.
Таким образом, при разгоне механизма вращения пусковой момент MП на валу двигателя преодолевает момент MС, а также момент сопротивления ![]() от инерции вращающихся частей привода:
от инерции вращающихся частей привода:
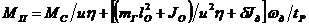 (6.2)
(6.2)
Умножив величину MП на передаточное число и КПД механизма вращения, получим 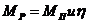 . С учетом выражения (6.2) получим динамический момент, действующий на поворотную часть крана при разгоне:
. С учетом выражения (6.2) получим динамический момент, действующий на поворотную часть крана при разгоне:
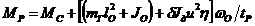 , (6.3)
, (6.3)
где ωО – угловая скорость поворотной части машины.
Избыточный момент, действующий на поворотную часть крана
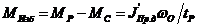 ,
,
где ![]() — приведенный к оси ротора двигателя момент инерции механизма вращения и груза при разгоне.
— приведенный к оси ротора двигателя момент инерции механизма вращения и груза при разгоне.
Максимальный динамический момент, действующий на поворотную часть при разгоне,
![]() (6.4)
(6.4)
Источником динамического нагружения поворотной части крана при торможении является тормозящий момент:
![]() (6.5)
(6.5)
где ![]() и
и ![]() — соответственно передаточное число, КПД и время торможения механизма вращения.
— соответственно передаточное число, КПД и время торможения механизма вращения.
Максимальный динамический момент, действующий на поворотную часть машины при ее торможении:
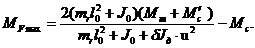 (6.6)
(6.6)
Основная литература [6, c.272…276]
Дополнительная литература [10, c.190…192]
Контрольные вопросы:
1. Назовите нагрузки, которые преодолевает пусковой момент на валу двигателя при разгоне механизма вращения
2. Напишите выражение динамического момента, действующего на поворотную часть крана при разгоне.
3. По какой зависимости определяют максимальный динамический момент, действующий на поворотную часть крана при торможении?
Лекция 7
Динамика ленточных конвейеров при переходных режимах работы
Динамика ленточных конвейеров зависит от характера транспортируе — мого груза, формы прогиба ленты под действием больших кусков, ударов кусков по ленте и роликоопорам при загрузке и других эксплуатационных факторов. В конвейерах динамические процессы возникают в режимах установившегося и не установившегося движений.
В период пуска в приводе конвейера, кроме статических, возникают инерционные нагрузки, на которые должен быть рассчитан двигатель. Из-за упругого удлинения ленты не все массы конвейера приходят в движение одновременно во время пуска двигателя.
Максимальное тяговое усилие на барабане
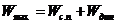 , (7.1)
, (7.1)
где ![]() — статическое тяговое усилие в период пуска; W
— статическое тяговое усилие в период пуска; W![]() > W
> W![]() ,
,
так как в период пуска коэффициент сопротивления движению ленты по роликоопорам Wп больше, чем при установившемся режиме W![]() = К
= К![]() •W; К
•W; К![]() =1,5 – коэффициент кратности статических сопротивлений трения при пуске; W
=1,5 – коэффициент кратности статических сопротивлений трения при пуске; W![]() – тяговое усилие в ленте при установившемся режиме.
– тяговое усилие в ленте при установившемся режиме.
Динамический момент при пуске привода
Mд = Jпр·ω/![]() , (7.2)
, (7.2)
где ω – угловая скорость вала двигателя; ![]() — время пуска привода; Jпр – приведенный к валу двигателя момент инерции движущихся масс конвейера:
— время пуска привода; Jпр – приведенный к валу двигателя момент инерции движущихся масс конвейера:


