Закон Ома для цепи переменного тока
L21теор, мГн
0
1
…
ПРИЛОЖЕНИЕ
Закон Ома для цепи переменного тока
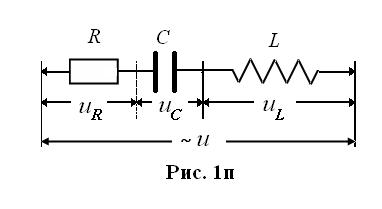 Рассмотрим цепь (рис. 1п), состоящую из активного сопротивления R, конденсатора C и индуктивности L, соединенных последовательно. Пусть на концы этой цепи подано переменное напряжение u циклической частоты w. В результате в цепи возникнет переменный ток той же частоты. Найдем закон, связывающий максимальные значения тока Im и напряжения Um. Пусть закон, по которому изменя-ется сила тока в данной це-пи, имеет вид i = Im cos wt, тогда изменение общего на-пряжения на концах цепи будет определяться выраже-нием u = Um cos (wt + j). Наличие слагаемого j, характеризующего разность фаз между током и напряжением, связано с тем, что напряжения на активном сопротивлении, емкости и индуктивности имеют вид
Рассмотрим цепь (рис. 1п), состоящую из активного сопротивления R, конденсатора C и индуктивности L, соединенных последовательно. Пусть на концы этой цепи подано переменное напряжение u циклической частоты w. В результате в цепи возникнет переменный ток той же частоты. Найдем закон, связывающий максимальные значения тока Im и напряжения Um. Пусть закон, по которому изменя-ется сила тока в данной це-пи, имеет вид i = Im cos wt, тогда изменение общего на-пряжения на концах цепи будет определяться выраже-нием u = Um cos (wt + j). Наличие слагаемого j, характеризующего разность фаз между током и напряжением, связано с тем, что напряжения на активном сопротивлении, емкости и индуктивности имеют вид
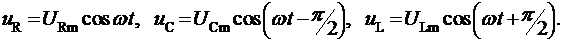
Это означает, что изменение напряжения на активном сопротивлении совпадает по фазе с изменением силы тока, изменение напряжения на емкости отстает от изменения тока на p/2, а на индуктивности опережает на p/2.
Суммирование величин uR, uC, и uL, которое определяет вид напряжения u, это довольно трудоемкая процедура. Чтобы упростить ее, воспользуемся векторной диаграммой. Для этого введем векторы UR, UC, UL и I, модули которых равны величинам URm, UСm, ULm и Im, соответственно. Начала векторов UR, UC, UL и I находятся в одной и той же точке O, а концы вращаются вокруг нее с угловой скоростью w, причем ориентация этих векторов в каждый момент времени определяется фазой колебания напряжения на R, C или L. Для того, чтобы определить вектор U, соответствующий амплитуде напряжения Um на концах рассматриваемой цепи, необходимо сложить векторы UR, UC и UL в какой-то фиксированный момент времени (например, в момент t = 0). Угол j между векторами U и I при этом определяет разность фаз между током и напряжением (см. рис. 2п).
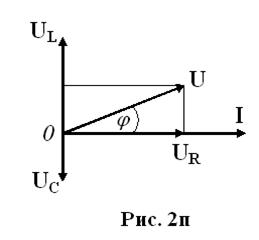 Из этого рисунка видно, что
Из этого рисунка видно, что
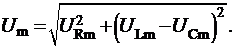 (2.1п)
(2.1п)
При этом, как известно, величины ULm, UCm и URm связаны с Im так:
![]() (2.2п)
(2.2п)
![]()
![]() (2.3п)
(2.3п)
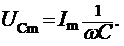 (2.4п)
(2.4п)
Подставив соотношения (2.2п.)![]() (2.4п) в формулу (2.1п), получим
(2.4п) в формулу (2.1п), получим
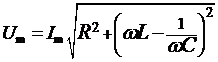 . (2.5п)
. (2.5п)
Формула (2.5п), определяющая связь величин Um и Im, называется законом Ома для цепи переменного тока. Величина 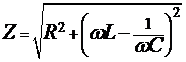 называется полным сопротивлением такой цепи.
называется полным сопротивлением такой цепи.
Разность фаз j между током и напряжением, как видно из того же рисунка, определяется соотношением
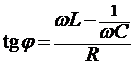 . (2.6п)
. (2.6п)
Контрольные вопросы
1. Сформулировать закон электромагнитной индукции Фарадея.
1. Сформулировать правило Ленца.
2. В чем заключается явление самоиндукции?
3. Вывести формулу для индуктивности бесконечного соленоида.
4. Почему при последовательном соединении двух катушек их взаимная индукция может иметь два различных значения?
5. Записать закон Ома для цепи переменного тока, содержащей активное сопротивление и индуктивность.
6. Записать формулу для расчета разности фаз, существующей меж — ду силой тока и напряжением в цепи, содержащей R, C и L.
7. Записать выражение для мощности переменного тока, выделяющейся в цепи с R и L.
8. Что такое максимальное и действующее значение силы переменного тока?
Литература
1. А. В. Астахов, Ю. М. Широков. Курс физики. М.: «Наука», 1980. Т. II. 359 с.
2. Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике. М.: «Мир», 1966. Вып. 5. 296 с.
3. Д. В. Сивухин. Общий курс физики. Т. III. Электричество. М.: «Наука», 1977. 688 с.
4. И. Е. Иродов. Электромагнетизм. Основные законы. М.-СПб.: Физматлит, 2000. 350 с.
Лабораторная работа Э.7
ИЗУЧЕНИЕ МАГНИТНЫХ СВОЙСТВ
ФЕРРОМАГНЕТИКОВ
Цель работы
Измерение магнитного поля и магнитной проницаемости ферромагнетика, изучение проявлений эффекта магнитного гистерезиса.
Теоретическое введение
Все вещества способны создавать магнитные поля и взаимодействовать с внешними магнитными полями. Иначе говоря, всякое вещество обладает магнитными свойствами. Это связано с тем, что по отношению к взаимодействию с магнитным полем любое вещество как макроскопическая система представляет собой скопление огромного числа микроскопических магнитных моментов.
Основной характеристикой магнитного состояния вещества как макросистемы является его намагниченность М. Если dV ![]() физически бесконечно малый объем вещества, сохраняющий при этом его макроскопические свойства и находящийся в точке с радиус-вектором r, то произведение М(r,t) dV совпадает с усредненным суммарным значением всех микроскопических магнитных моментов, принадлежащих объему dV в момент времени t (в общем случае состояние вещества может быть неоднородным и нестационарным, что и обусловливает возможную зависимость М и от r, и от t). Так как в СИ магнитный момент измеряется в А. м2, то единицей измерения намагниченности является А/м.
физически бесконечно малый объем вещества, сохраняющий при этом его макроскопические свойства и находящийся в точке с радиус-вектором r, то произведение М(r,t) dV совпадает с усредненным суммарным значением всех микроскопических магнитных моментов, принадлежащих объему dV в момент времени t (в общем случае состояние вещества может быть неоднородным и нестационарным, что и обусловливает возможную зависимость М и от r, и от t). Так как в СИ магнитный момент измеряется в А. м2, то единицей измерения намагниченности является А/м.
Вещество, у которого всюду намагниченность М равна 0, называют ненамагниченным (или размагниченным). В противном случае говорят, что вещество намагничено. Переход из первого состояния во второе называется процессом намагничивания.
Микроскопические магнитные моменты обусловлены электронами атомов и молекул вещества. Каждый электрон, перемещаясь внутри этих мельчайших частиц вещества, во-первых, создает микроскопически малый ток, который характеризуется микроскопически малым магнитным моментом, и, во-вторых, обладает так называемым собственным магнитным моментом (им обладает покоящийся электрон и даже нейтрон, который не имеет заряда). Их происхождение сугубо квантовое.
В мельчайших частицах вещества возможны две ситуации. В одной из них, в отсутствие внешнего магнитного поля, магнитные моменты разных электронов в сумме компенсируют друг друга. Такая частица в целом магнитного момента не имеет. Атомы и молекулы этого типа называются диамагнитными, аналогично именуют и состоящие из них вещества. Иначе их называют диамагнетиками. В отсутствие внешних магнитных полей намагниченность диамагнетика равна нулю. Он ненамагничен.
Если только что упомянутой компенсации не происходит, то соответствующая мельчайшая частица вещества называется парамагнитной и парамагнитным или парамагнетиком называется вещество, состоящее из таких частиц. Из-за хаотичности теплового движения при отсутствии внешних магнитных полей магнитные моменты парамагнитных частиц ориентированы беспорядочно. Из-за этого при суммировании макроскопически большого числа этих моментов получается нуль. Следовательно, и в этом случае намагниченность равна нулю, т. е. парамагнетик размагничен.
Наконец, существует класс твердых сред, разительно отличающихся от диа — и парамагнитных материалов. Из таких сред наиболее распространенным является железо. Поэтому их стали называть ферромагнитными или ферромагнетиками. В них и при отсутствии внешних магнитных полей существуют участки макроскопических размеров, в которых суммы всех входящих в них микроскопических моментов не равны нулю. Это связано с особенностями атомно-молекулярных взаимодействий в таких средах, из-за чего разным микроскопическим моментам, образующих макросистему, энергетически не выгодно ориентироваться беспорядочно (как, например, в парамагнетиках). Они выстроены преимущественно в одном каком-то порядке. Такие области в веществе называются магнитными доменами. В них самопроизвольно или спонтанно существует ненулевая намагниченность. Часто количества ферромагнитного вещества оказывается достаточно много в том смысле, что в таком веществе формируется много доменов с разными ориентациями их намагниченностей. Тогда суммарный магнитный момент всего объема вещества снова оказывается нулевым. В этом случае в целом ферромагнетик размагничен несмотря на то, что в пределах каждого домена это не так.


