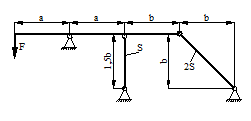
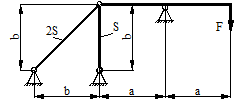
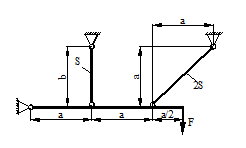
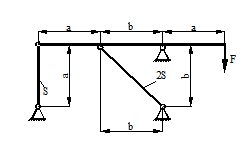
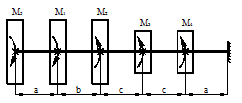
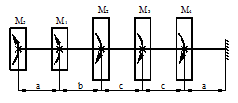
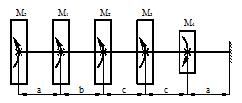
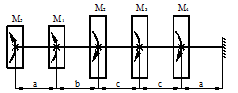
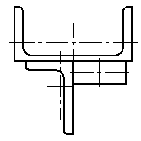
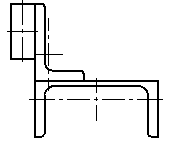
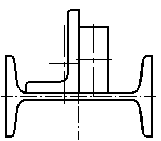
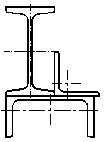
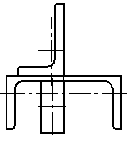
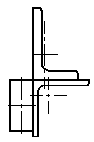
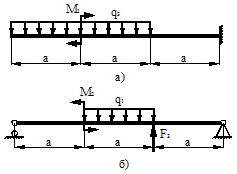
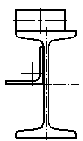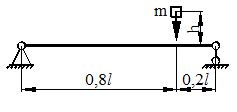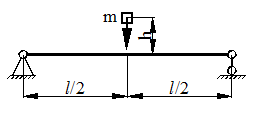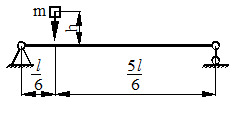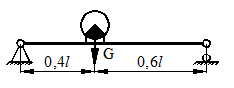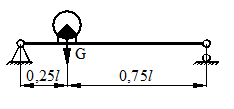Статический прогиб балки
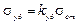 ,
, 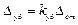 ,
,
где sуд, sст – напряжения при ударном и статическом нагружении;
kуд – ударный коэффициент;
∆уд, ∆ст – прогибы при ударном и статическом нагружении.
Ударный коэффициент определяется по формуле:
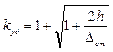 ,
,
где h – высота падения груза.
ПРИМЕР
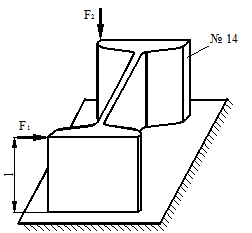
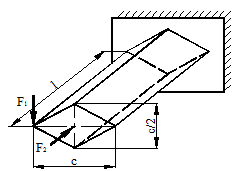
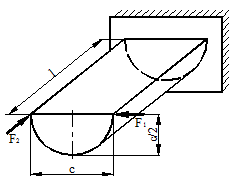
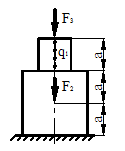
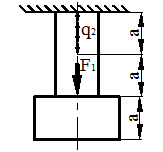
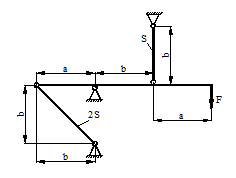
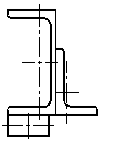
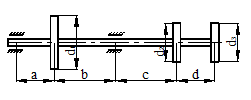
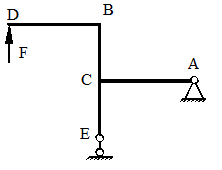
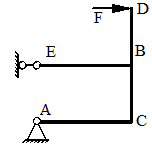
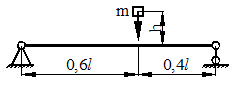
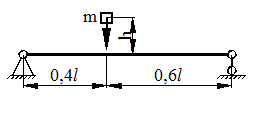
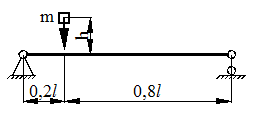
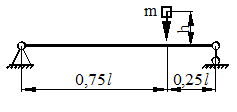
Для схемы, показанной на рис. 40, определить максимальные ударные напряжения и максимальный прогиб, если масса падающего груза m = 50 кГ, высота падения h = 40 мм, сечение балки – двутавр № 14: WX = 81,7 см3, IX = = 572 см4, материал балки – сталь.
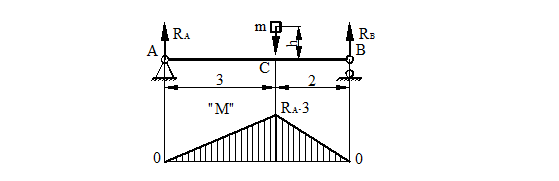
Рисунок 40.
1) Определяем опорные реакции
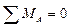 ;
; 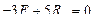
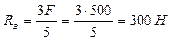
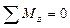 ;
; 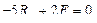
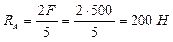
Проверка
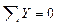 ;
; 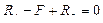
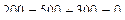 — верно
— верно
2) Определяем статический прогиб балки
Прогиб балки определим по методу начальных параметров.
a. Составляем уравнение прогибов для точки С
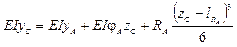
b. Определяем начальные параметры
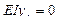 . Для нахождения
. Для нахождения ![]() составим уравнение прогибов для точки В, приравняв его к нулю, найдем искомую величину.
составим уравнение прогибов для точки В, приравняв его к нулю, найдем искомую величину.
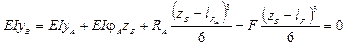
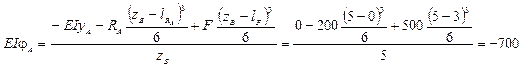
c. Находим прогиб в точке С
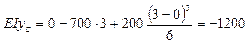
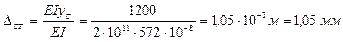
3) Определяем ударный коэффициент
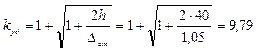
4) Определяем напряжения в балке от статического действия нагрузки
Изгибающий момент будет иметь максимальное значение в точке С, а его величина определится по формуле (рис. 40):
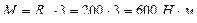
Тогда напряжения в точке С:
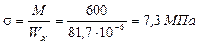
5) Определяем динамический прогиб и напряжения
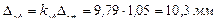
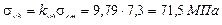
Указания к задаче 11
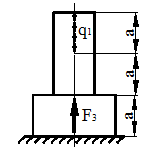
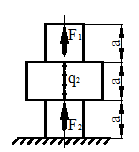
Если упругую балку вывести из положения равновесия, а затем резко снять нагрузку, то под действием сил упругости, балка начнет совершать колебания из крайнего нижнего в крайнее верхнее положение (рис. 41). Такие колебания называются свободными колебаниями. Если же колебания системы вызываются действием периодической внешней силы, то такие колебания называются вынужденными.
Балку, к которой прикреплен груз, намного превышающий вес самой
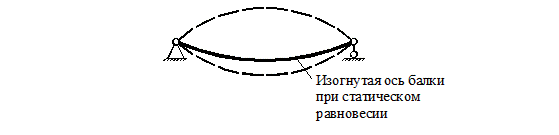
Рисунок 41.

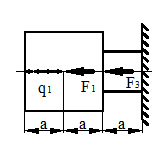
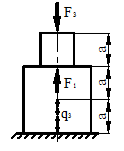
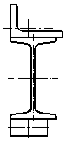
Рисунок 42.
балки, можно рассматривать как невесомую, пренебрегая ее собственным весом (рис. 42). В балке, показанной на рис. 42, положение любого поперечного сечения в любой момент времени можно определить, зная положение хотя бы одного поперечного сечения в начальный момент времени. Такая балка представляет собой систему с одной степенью свободы.
Уравнение свободных (собственных) колебаний системы с одной степенью свободы записывается следующим образом:
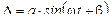 ,
,
где D — прогиб балки под грузом;
а – амплитуда свободных колебаний;
w – частота свободных колебаний системы, совершаемых за 2p сек;
t – время;
b — начальная фаза колебаний.
Частота свободных колебаний системы определяется по формуле:
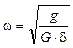 ,
,
где g — ускорение свободного падения;
G – вес груза;
d — перемещение от единичной силы.
Промежуток времени, за который система совершает одно свободное колебание, называется периодом свободных колебаний, который определяется по формуле:
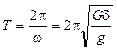 .
.
Если на балку действует внешняя сила, изменяющаяся по закону 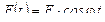 , то система совершает вынужденные колебания, уравнение которых записывается в виде:
, то система совершает вынужденные колебания, уравнение которых записывается в виде:
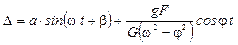 ,
,
где j — круговая частота возмущающей силы.
Амплитуда вынужденных колебаний системы определяется по формуле:
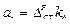 ,
,
где ![]() — статический прогиб балки под действием возмущающей силы;
— статический прогиб балки под действием возмущающей силы;
kд – динамический коэффициент.
Статический прогиб балки от действия возмущающей силы определяется по формуле:
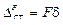 .
.
Динамический коэффициент определяется по формуле:
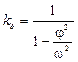 .
.
Динамические напряжения, вызванные периодической возмущающей силой, определяются по формуле:
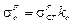 ,
,
где ![]() — напряжения, вызванные статическим действием силы F.
— напряжения, вызванные статическим действием силы F.
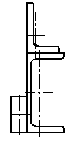
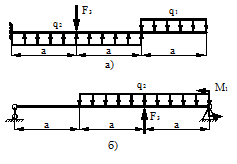
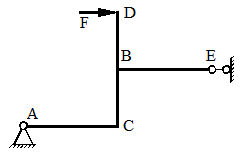
ПРИМЕР
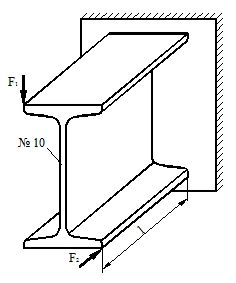
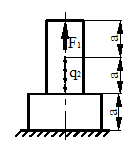
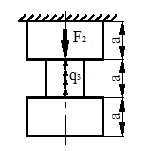
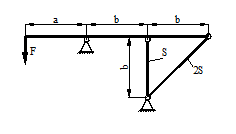
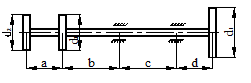
На стальной балке, показанной на рис. 43, установлен электродвигатель весом G = 20 кН, совершающий n = 500 об/мин. Центробежная сила, возникающая вследствие неуравновешенности частей двигателя составляет F = =0,2G. Подобрать двутавровое поперечное сечение балки из условия отстройки от резонанса 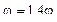 , определить максимальный прогиб и максимальные напряжения. Собственный вес балки не учитывается l = 1 м.
, определить максимальный прогиб и максимальные напряжения. Собственный вес балки не учитывается l = 1 м.
7.3) Находим частоту вынужденных колебаний.
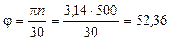 с-1
с-1
8.3) Определяем частоту свободных колебаний из условия отстройки от резонанса.
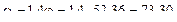 с-1
с-1
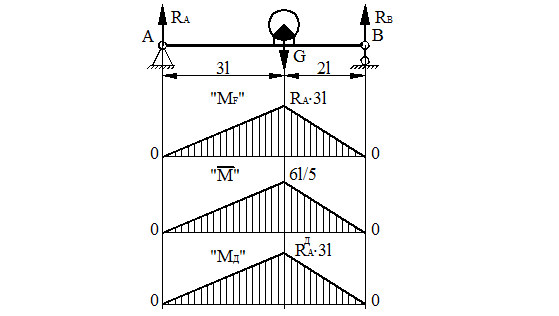
Рисунок 43.
9.3) Определяем прогиб от единичной силы по способу Верещагина
Эпюра момента от действия единичной силы показана на рис. 43. Для нахождения прогиба перемножаем эту эпюру саму на себя.
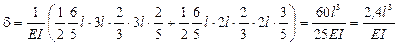
10.3) Подбираем поперечное сечение
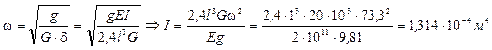
По ГОСТ 8239 – 89 подбираем двутавр № 36: IX = 13380 см4, WX = =743см3.
11.3) Определяем частоту свободных колебаний системы
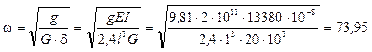 с-1
с-1
12.3) Определяем динамический коэффициент
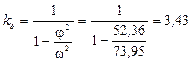
13.3) Определяем наибольшие напряжения в балке
1) Определяем напряжения от веса двигателя
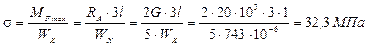
1) Определяем напряжения от статического действия центробежной силы
Так как 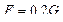 , то статические напряжения от F найдем по формуле:
, то статические напряжения от F найдем по формуле:

1) Определяем динамические напряжения от центробежной силы
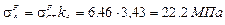
2.1) Определяем полные напряжения
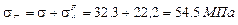
14.3) Определяем наибольший прогиб балки
2) Определяем статический прогиб от действия центробежной силы
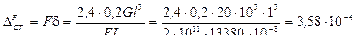 м
м
2) Определяем динамический прогиб от действия центробежной силы
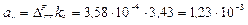 м
м
2) Определяем статический прогиб балки от веса двигателя
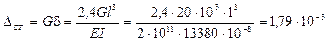 м
м
3.1) Определяем полный прогиб
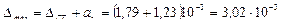 м
м
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
Выполняя контрольную работу, необходимо соблюдать следующие требования:
1) контрольная работа выполняется в ученической тетради синими чернилами, четким почерком с полями в 4 см для возможных замечаний рецензента;
2) на обложке тетради указать фамилию, имя, отчество, шифр, наименование предмета, номер контрольной работы, почтовый адрес с индексом отделения связи;
3) данные из таблиц для выполнения контрольной работы нужно брать в соответствии с личным шифром студента и первыми пятью буквами русского алфавита, которые следует расположить под шифром. Например, Ваш шифр 12345, тогда
|
шифр |
1 |
2 |
3 |
4 |
5 |
|
буквы |
а |
б |
в |
г |
д |
К каждой задаче контрольной работы дается таблица с исходными данными. Вертикальные столбцы этой таблицы обозначены буквами, а крайний левый столбец обозначает номер строки. Из каждого вертикального столбца таблицы (обозначен буквой) необходимо взять только одно значение, стоящее в горизонтальной строке, номер которой соответствует цифре вашего шифра, стоящей над буквой.
4) перед решением каждой задачи надо выписать ее условия с числовыми данными, а также выполнить соответствующий чертеж с указанием всех необходимых размеров и величин;
5) решение должно сопровождаться краткими последовательными и грамотными пояснениями, с указанием размерности всех получаемых величин;
6) вычисления должны производится с точностью то трех значащих цифр;
7) каждую задачу необходимо решать с новой страницы;
8) по получении проверенной контрольной работы студент должен исправить в ней все ошибки, сохраняя предыдущие неверные записи.
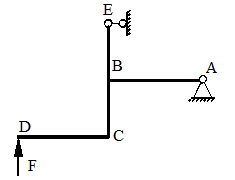
ЗАДАЧА 1
Для схемы, показанной на рисунке (табл. 2) необходимо:
Вычертить ее в произвольном масштабе.
Для произвольного поперечного сечения стержня записать уравнения внутренних силовых факторов.
Построить эпюры внутренних силовых факторов.
Таблица 1
Исходные данные к задаче № 1
|
№ п/п |
l, м |
с, м |
F1, кН |
F2, кН |
номер схемы |
|
1 |
1,1 |
0,2 |
10 |
25 |
1 |
|
2 |
1,2 |
0,3 |
15 |
30 |
2 |
|
3 |
1,3 |
0,4 |
20 |
15 |
3 |
|
4 |
1,4 |
0,5 |
25 |
20 |
4 |
|
5 |
1,5 |
0,6 |
30 |
25 |
5 |
|
6 |
1,6 |
0,7 |
10 |
15 |
6 |
|
7 |
1,7 |
0,8 |
15 |
20 |
7 |
|
8 |
1,8 |
0,9 |
20 |
30 |
8 |
|
9 |
1,9 |
0,4 |
25 |
10 |
9 |
|
0 |
2,0 |
0,7 |
30 |
20 |
10 |
|
а |
б |
в |
г |
д |
Таблица 2
Расчетные схемы к задаче №1
|
1 |
|
6 |
|
|
Продолжение таблицы 2 |
|||
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
Продолжение таблицы 2 |
|||
|
5 |
|
10 |
|
ЗАДАЧА 2
Для вертикального стержня, имеющего жесткую заделку на одном из концов, изображенного на рисунке (табл. 4) необходимо:
Вычертить схему в произвольном масштабе.
Определить значения нормальной силы на каждом участке стержня.
Построить эпюру нормальной силы.
Определить удлинение стержня.
Длины участков стержня и нагрузки, приложенные к нему, приведены в табл. 3, площадь поперечного сечения узкого участка S = 0,2 м2, широкого участка 2S.
Таблица 3
Исходные данные к задаче № 2
|
№ п/п |
а, м |
q1=q3, кН/м |
q2, кН/м |
F1, кН |
F2, кН |
F3, кН |
номер схемы |
|
1 |
0,8 |
5 |
30 |
10 |
35 |
10 |
1 |
|
2 |
1 |
10 |
25 |
15 |
30 |
20 |
2 |
|
3 |
1,2 |
15 |
20 |
20 |
25 |
30 |
3 |
|
4 |
1,4 |
20 |
15 |
25 |
20 |
40 |
4 |
|
5 |
1,6 |
25 |
10 |
30 |
15 |
10 |
5 |
|
6 |
1,8 |
30 |
5 |
35 |
10 |
20 |
6 |
|
7 |
2 |
5 |
30 |
40 |
5 |
30 |
7 |
|
8 |
0,8 |
10 |
25 |
10 |
35 |
40 |
8 |
|
9 |
1 |
15 |
20 |
15 |
30 |
10 |
9 |
|
0 |
1,2 |
20 |
15 |
20 |
25 |
20 |
10 |
|
а |
д |
в |
г |
б |
в |
д |
Таблица 4
Расчетные схемы к задаче №2
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
5 |
|
10 |
|
ЗАДАЧА 3
Жесткий брус, шарнирно закрепленный одним концом и подкрепленный двумя упругими стержнями, нагружен известной силой (табл. 6). Для заданной конструкции требуется:
1) Вычертить ее схему в произвольном масштабе.
2) Рассчитать безопасные размеры стержней и подобрать в таблицах ГОСТа необходимые размеры равнополочных или неравнополочных уголков.
3) Рассчитать напряжения в стержнях, допустив, что один из них изготовлен на величину D короче, то есть, найти монтажные напряжения.
4) Рассчитать напряжения в стержнях, возникающие от изменения температуры.
5) Найти суммарные напряжения в стержнях от внешней силы, от неточности монтажа, от изменения температуры.
6) Подсчитать недонапряжение или перенапряжение стержней.
Примечание: принять модуль Юнга Е = 2∙105 МПа, коэффициент линейного расширения a=125∙10-7 1/°С.
Числовые данные взять из таблицы 5.
Таблица 5
Исходные данные к задаче № 3
|
№ п/п |
а, м |
b, м |
F, кН |
∆, мм |
∆t, °С |
[s], МПа |
номер схемы |
|
1 |
1,5 |
1,7 |
60 |
0,2 |
20 |
90 |
1 |
|
2 |
1,4 |
1,6 |
65 |
0,3 |
30 |
100 |
2 |
|
3 |
1,3 |
1,5 |
70 |
0,4 |
40 |
110 |
3 |
|
4 |
1,2 |
1,4 |
75 |
0,2 |
25 |
120 |
4 |
|
5 |
1,0 |
1,3 |
80 |
0,1 |
35 |
140 |
5 |
|
6 |
0,9 |
1,2 |
85 |
0,4 |
20 |
90 |
6 |
|
7 |
0,8 |
1,1 |
90 |
0,2 |
25 |
100 |
7 |
|
8 |
1,2 |
1,0 |
60 |
0,3 |
30 |
120 |
8 |
|
9 |
1,4 |
0,8 |
80 |
0,4 |
35 |
140 |
9 |
|
0 |
1,3 |
1,0 |
100 |
0,5 |
40 |
120 |
10 |
|
а |
б |
в |
г |
д |
а |
д |
Таблица 6
Расчетные схемы к задаче № 3
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
5 |
|
10 |
|
ЗАДАЧА 4
Для заданной расчетной схемы (табл. 8) необходимо:
1) Вычертить расчетную схему вала в произвольном масштабе.
2) Построить эпюру крутящих моментов.
3) Из условия прочности определить размеры поперечного сечения вала, приняв сечение вала круглым, кольцевым, прямоугольным.
4) Построить эпюру углов закручивания для круглого вала, приняв жесткость сечения постоянной.
5) Сравнить веса валов.
Числовые данные взять из таблицы 7.
Таблица 7
Исходные данные к задаче № 4
|
№ п/п |
М1, Н∙м |
М2, Н∙м |
М3, Н∙м |
М4, Н∙м |
М5, Н∙м |
[t], МПа |
а, м |
b, м |
с, м |
|
|
№ схе-мы |
|
1 |
100 |
500 |
800 |
400 |
600 |
50 |
0,2 |
0,7 |
0,5 |
0,4 |
1,1 |
1 |
|
2 |
200 |
600 |
700 |
300 |
500 |
60 |
0,3 |
0,6 |
0,6 |
0,5 |
1,2 |
2 |
|
3 |
300 |
700 |
600 |
800 |
300 |
70 |
0,4 |
0,5 |
0,4 |
0,6 |
1,3 |
3 |
|
4 |
400 |
800 |
500 |
700 |
200 |
80 |
0,5 |
0,4 |
0,3 |
0,7 |
1,4 |
4 |
|
5 |
500 |
900 |
400 |
600 |
700 |
90 |
0,6 |
0,3 |
0,5 |
0,8 |
1,5 |
5 |
|
6 |
600 |
1000 |
300 |
500 |
800 |
50 |
0,7 |
0,2 |
0,8 |
0,9 |
1,6 |
6 |
|
7 |
700 |
900 |
200 |
600 |
900 |
60 |
0,8 |
0,3 |
0,7 |
0,8 |
1,7 |
7 |
|
8 |
800 |
800 |
100 |
300 |
1000 |
70 |
0,7 |
0,4 |
0,3 |
0,7 |
1,8 |
8 |
|
9 |
900 |
700 |
1000 |
200 |
400 |
80 |
0,6 |
0,5 |
0,4 |
0,6 |
1,9 |
9 |
|
0 |
1000 |
100 |
900 |
300 |
100 |
90 |
0,5 |
0,6 |
0,2 |
0,5 |
2,0 |
10 |
|
д |
г |
в |
б |
г |
а |
д |
г |
в |
б |
а |
д |
Таблица 8
Расчетные схемы к задаче № 4
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
5 |
|
10 |
|
ЗАДАЧА 5
Для заданных схем (табл. 9) необходимо:
7.1) Вычертить поперечное сечение в строгом масштабе.
8.1) Определить положение центра тяжести.
9.1) Найти величины осевых моментов инерции относительно центральных осей.
10.1) Найти величину центробежного момента инерции относительно центральных осей.
11.1) Определить положение главных осей инерции.
12.1) Найти главные моменты инерции.
Числовые данные взять из табл. 10.
Таблица 9
Расчетные схемы к задаче № 5
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
5 |
|
10 |
|
Таблица 10
Исходные данные к задаче № 5
|
№ |
Уголок равнополочный |
Уголок неравнополочный |
Двутавр |
Швеллер |
Прямо-угольник |
№ схемы |
|
1 |
30´5 |
50´32´4 |
10 |
8 |
100´30 |
1 |
|
2 |
40´6 |
56´36´4 |
12 |
10 |
100´40 |
2 |
|
3 |
50´4 |
63´40´8 |
14 |
12 |
100´20 |
3 |
|
4 |
56´4 |
70´45´5 |
16 |
14 |
80´40 |
4 |
|
5 |
63´6 |
80´50´6 |
18 |
14а |
80´60 |
5 |
|
6 |
70´8 |
90´56´6 |
20 |
16 |
80´100 |
6 |
|
7 |
80´8 |
100´63´6 |
20а |
16а |
80´20 |
7 |
|
8 |
90´9 |
90´56´8 |
22 |
18 |
60´40 |
8 |
|
9 |
75´9 |
140´90´10 |
22а |
18а |
60´60 |
9 |
|
0 |
100´10 |
160´100´12 |
27 |
20 |
60´40 |
10 |
|
д |
а |
б |
в |
г |
д |
ЗАДАЧА 6
Для заданных схем балок (табл. 12) построить эпюры поперечной силы Q и изгибающего момента М. Подобрать поперечное сечение для схемы а) круглое [s] = 10 МПа; б) двутавровое [s] = 150 МПа.
Числовые данные взять из табл. 11.
Таблица 11
Исходные данные к задаче № 6
|
№ |
а, м |
q1=q3, кН/м |
q2, кН/м |
F1, кН |
F2, кН |
F3, кН |
М1, кН∙м |
М2, кН∙м |
М3, кН∙м |
№ схемы |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
1 |
0,8 |
5 |
30 |
10 |
35 |
10 |
10 |
35 |
10 |
1 |
|
2 |
1 |
10 |
25 |
15 |
30 |
20 |
15 |
30 |
20 |
2 |
|
3 |
1,2 |
15 |
20 |
20 |
25 |
30 |
20 |
25 |
30 |
3 |
|
4 |
1,4 |
20 |
15 |
25 |
20 |
40 |
25 |
20 |
40 |
4 |
|
5 |
1,6 |
25 |
10 |
30 |
15 |
10 |
30 |
15 |
10 |
5 |
|
6 |
1,8 |
30 |
5 |
35 |
10 |
20 |
35 |
10 |
20 |
6 |
|
7 |
2 |
5 |
30 |
40 |
5 |
30 |
40 |
5 |
30 |
7 |
|
Продолжение таблицы 11 |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
8 |
0,8 |
10 |
25 |
10 |
35 |
40 |
10 |
35 |
40 |
8 |
|
9 |
1 |
15 |
20 |
15 |
30 |
10 |
15 |
30 |
10 |
9 |
|
0 |
1,2 |
20 |
15 |
20 |
25 |
20 |
20 |
25 |
20 |
10 |
|
б |
в |
г |
д |
а |
б |
в |
г |
д |
д |
Таблица 12
Расчетные схемы к задаче № 6
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
Продолжение таблицы 12 |
|||
|
4 |
|
9 |
|
|
5 |
|
10 |
|
ЗАДАЧА 7
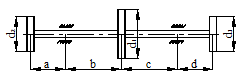
Вал, показанный на схеме (табл. 13) имеет три жестко насаженных шкива. Ведущий шкив диаметром d1 с углом наклона ремня к горизонту a1 (рис. 44) передает мощность N при n оборотах в минуту. Два ведомых шкива имеют одинаковые диаметры d2 = d3 и одинаковые углы наклона ремней к горизонту a1 = a2, каждый из них передает мощность N/2.
Необходимо:
7.2) Определить скручивающие моменты, приложенные к шкивам.
8.2) Построить эпюру крутящего момента.
9.2) Определить силы, действующие на вал со стороны ремней в горизонтальной и вертикальной плоскости.
10.2) Построить эпюры изгибающих моментов в горизонтальной и вертикальной плоскости.
11.2) Построить суммарную эпюру изгибающего момента.
12.2) Подобрать безопасное сечение вала.
Числовые данные взять из табл. 14.
Таблица 13
Расчетные схемы к задаче № 7
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
5 |
|
10 |
|
Таблица 14
Исходные данные к задаче № 7
|
№ |
N, кВт |
n, об/мин |
а, мм |
b, мм |
с, мм |
d, мм |
d1, мм |
d2, мм |
a1° |
a2° |
№ схемы |
|
1 |
5 |
100 |
150 |
600 |
150 |
500 |
400 |
200 |
10 |
10 |
1 |
|
2 |
10 |
200 |
200 |
550 |
600 |
450 |
420 |
220 |
20 |
20 |
2 |
|
3 |
15 |
300 |
250 |
500 |
200 |
400 |
440 |
240 |
30 |
30 |
3 |
|
4 |
20 |
400 |
300 |
450 |
550 |
350 |
460 |
260 |
40 |
40 |
4 |
|
5 |
25 |
500 |
350 |
400 |
250 |
300 |
480 |
280 |
50 |
50 |
5 |
|
6 |
30 |
600 |
400 |
350 |
300 |
250 |
500 |
300 |
60 |
60 |
6 |
|
7 |
35 |
700 |
450 |
300 |
350 |
550 |
520 |
320 |
70 |
70 |
7 |
|
8 |
40 |
800 |
500 |
250 |
400 |
200 |
540 |
340 |
80 |
80 |
8 |
|
9 |
45 |
900 |
550 |
200 |
450 |
600 |
560 |
360 |
90 |
90 |
9 |
|
0 |
50 |
1000 |
600 |
150 |
500 |
150 |
580 |
380 |
0 |
0 |
10 |
|
г |
д |
а |
б |
в |
г |
д |
а |
б |
в |
д |
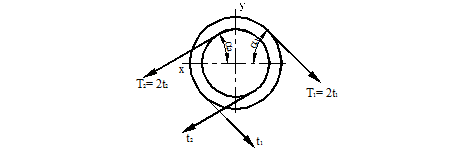
Рисунок 44.
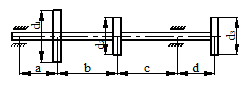
ЗАДАЧА 8
Подобрать поперечное сечение сжатого стержня большой длины при допускаемом напряжении на сжатие [s] = 150 МПа. Вид закрепления стержня показан на рис. 45. Данные взять из табл. 15.
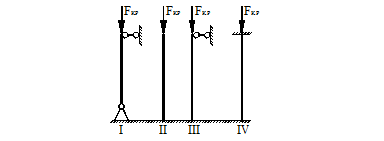
Рисунок 45.
Таблица 15
Исходные данные к задаче № 8
|
№ |
Вид закрепления |
F, кН |
l, м |
Форма поперечного сечения |
|
1 |
I |
50 |
6,5 |
Двутавр |
|
2 |
II |
60 |
6 |
Швеллер |
|
3 |
III |
70 |
5,5 |
Квадрат |
|
4 |
IV |
80 |
5 |
Окружность |
|
5 |
I |
90 |
4,5 |
Прямоугольник с соотношением сторон 1/2 |
|
6 |
II |
100 |
4 |
Двутавр |
|
7 |
III |
110 |
3,5 |
Швеллер |
|
8 |
IV |
120 |
3 |
Квадрат |
|
9 |
I |
130 |
2,5 |
Окружность |
|
0 |
II |
140 |
2 |
Прямоугольник с соотношением сторон 1/2 |
|
в |
д |
б |
г |
ЗАДАЧА 9
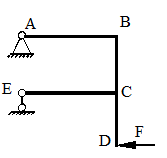
Для рамы, представленной на рисунке (табл. 17) необходимо:
Построить эпюры внутренних силовых факторов.
Определить горизонтальное и вертикальное перемещение заданного сечения.
Определить угол поворота заданного сечения.
Числовые данные взять из табл. 16. Жесткость сечения вертикальных и горизонтальных сечений рамы принять равной EI. Длина каждого из горизонтальных участков l, длина каждого из вертикальных участков h.
Таблица 16
Исходные данные к задаче № 9
|
№ |
F, кН |
h, м |
l, м |
сечение |
№ схемы |
|
1 |
20 |
1 |
2 |
b |
1 |
|
2 |
25 |
2 |
1 |
c |
2 |
|
3 |
30 |
3 |
4 |
b |
3 |
|
4 |
35 |
4 |
3 |
c |
4 |
|
5 |
40 |
5 |
2 |
b |
5 |
|
6 |
45 |
1 |
5 |
c |
6 |
|
7 |
50 |
2 |
3 |
b |
7 |
|
8 |
55 |
3 |
4 |
c |
8 |
|
9 |
60 |
4 |
5 |
b |
9 |
|
0 |
65 |
5 |
1 |
c |
10 |
|
в |
г |
в |
б |
д |
Таблица 17
Расчетные схемы к задаче № 9
|
1 |
|
6 |
|
|
Продолжение таблицы 17 |
|||
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
5 |
|
10 |
|
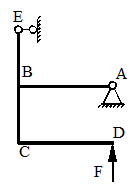
ЗАДАЧА 10
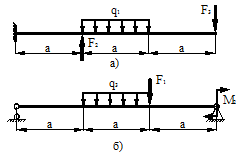
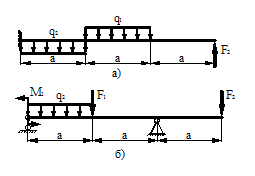
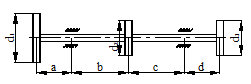
Для стальной двутавровой балки, изображенной на схеме (табл. 19), определить максимальные ударные напряжения и максимальный прогиб в месте падения груза. Числовые данные взять из табл. 18.
Таблица 18
Исходные данные к задаче № 10
|
№ |
m, кГ |
h, мм |
l, м |
№ двутавра |
№ схемы |
|
1 |
20 |
85 |
4 |
10 |
1 |
|
2 |
25 |
80 |
4,2 |
12 |
2 |
|
3 |
30 |
75 |
4,6 |
14 |
3 |
|
4 |
35 |
70 |
4,8 |
16 |
4 |
|
5 |
40 |
65 |
5,0 |
18 |
5 |
|
6 |
45 |
60 |
5,2 |
20 |
6 |
|
7 |
50 |
55 |
5,4 |
22 |
7 |
|
8 |
55 |
50 |
5,6 |
24 |
8 |
|
9 |
60 |
45 |
5,8 |
27 |
9 |
|
0 |
65 |
40 |
6,0 |
30 |
10 |
|
в |
г |
в |
б |
д |
Таблица 19
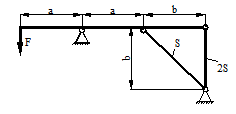
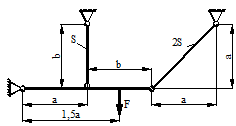
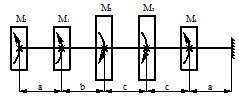
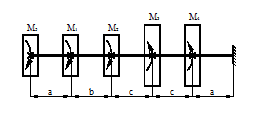
Расчетные схемы к задаче № 10
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
Продолжение таблицы 19 |
|||
|
4 |
|
9 |
|
|
5 |
|
10 |
|
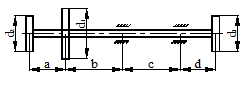
ЗАДАЧА 11
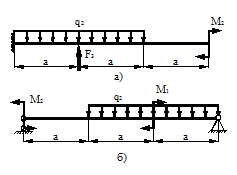
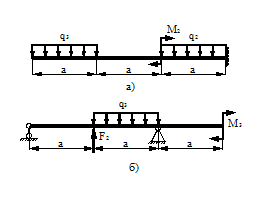
На стальной балке, показанной на схеме (табл. 21), установлен электродвигатель весом G, совершающий n об/мин. Центробежная сила, возникающая вследствие неуравновешенности частей двигателя составляет F =0,2G. Подобрать двутавровое поперечное сечение балки из условия отстройки от резонанса 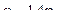 , определить максимальный прогиб и максимальные напряжения. Собственный вес балки не учитывается. Числовые данные взять из табл. 20.
, определить максимальный прогиб и максимальные напряжения. Собственный вес балки не учитывается. Числовые данные взять из табл. 20.
Таблица 20
Исходные данные к задаче № 11
|
№ |
G, кH |
n, об/мин |
l, м |
№ схемы |
|
1 |
60 |
200 |
4 |
1 |
|
2 |
55 |
250 |
4,2 |
2 |
|
3 |
40 |
300 |
4,6 |
3 |
|
4 |
35 |
350 |
4,8 |
4 |
|
5 |
30 |
400 |
5,0 |
5 |
|
6 |
25 |
450 |
5,2 |
6 |
|
7 |
20 |
500 |
5,4 |
7 |
|
8 |
15 |
550 |
5,6 |
8 |
|
9 |
30 |
600 |
5,8 |
9 |
|
0 |
25 |
650 |
6,0 |
10 |
|
д |
в |
б |
г |
Таблица 21
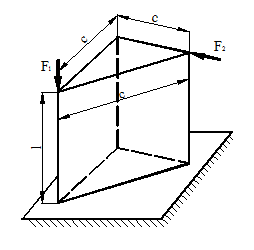
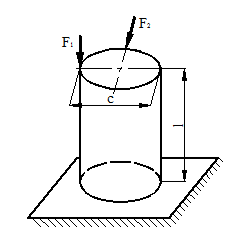
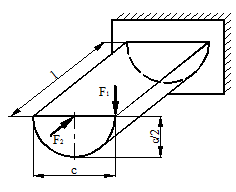
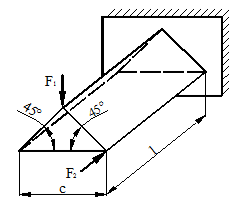
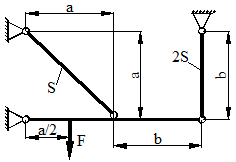
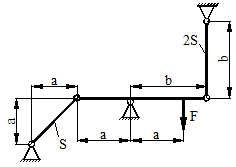
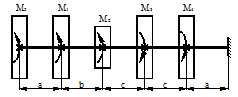
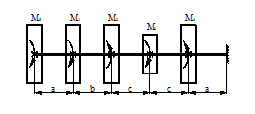
Расчетные схемы к задаче № 11
|
1 |
|
6 |
|
|
2 |
|
7 |
|
|
3 |
|
8 |
|
|
4 |
|
9 |
|
|
5 |
|
10 |
|
СОДЕРЖАНИЕ
Введение 3
Указания к задаче 1 4
Указания к задаче 2 6
Указания к задаче 3 9
Указания к задаче 4 16
Указания к задаче 5 20
Указания к задаче 6 28
Указания к задаче 7 40
Указания к задаче 8 44
Указания к задаче 9 49
Указания к задаче 10 57
Указания к задаче 11 60
Задания для контрольных работ 65
Задача 1 66
Задача 2 68
Задача 3 70
Задача 4 72
Задача 5 73
Задача 6 75
Задача 7 77
Задача 8 79
Задача 9 80
Задача 10 81
Задача 11 83
СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
Учебно-методическое пособие
для самостоятельной работы студентов
Составители: Ю. Ф. Загороднев, Л. В. Якименко, Д. Н. Пирожков
Публикуется в редакции составителей
Корректура составителей
ЛР № 020648 от 16 декабря 1997 г.
Издательство АГАУ
656099, г. Барнаул, пр. Красноармейский, 98
62-84-26