| Диэлектрическая восприимчивость

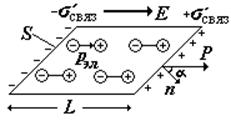
	полный заряд на поверхности S
	дипольный момент всего куска диэлектрика и его объем
	подставляя в (n) и сокращая, получим связь Р с s¢связ. Запишем в виде:
	Таким образом: нормальная составляющая вектора поляризации (Рn) численно равна поверхностной плотности связанных зарядов

··	Из опыта следует, что для многих диэлектриков при не очень сильных полях, вектор поляризации прямо пропорционален напряженности внешнего поля;

c — коэффициент пропорциональности — называется диэлектрической восприимчивостью диэлектрика, она зависит от плотности диэлектрика и температуры (c — греческая буква «хи»).

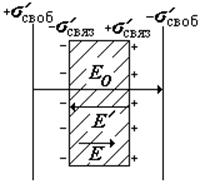
Поместим в поле плоского конденсатора, заряженного с поверхностной плотностью заряда s своб, кусок диэлектрика так, чтобы его поверхность была перпендикулярна силовым линиям поля (см. рис.). На поверхности диэлектрика появляются связанные заряды с поверхностной плотностью s¢связ. Напряженность поля конденсатора Е0, напряженность поля связанных зарядов Е¢. В соответствии с принципом суперпозиции:

результирующее поле внутри диэлектрика

напряженность поля связанных зарядов; подставим в (·) и, учтя (··), получим:

или

— диэлектрическая проницаемость – безразмерная величина, показывающая, во сколько раз уменьшается напряженность поля внутри диэлектрика по сравнению с вакуумом. [14]

e = 1 – вакуум

e @ 1 – воздух, газы

e > 1 — для всех диэлектриков

Электрическое поле в диэлектриках характеризуют также вспомогательным вектором D:

вектор электрической индукции (электрического смещения)

Вектор D физического смысла не имеет, но он удобен в случае, когда линии напряженности внешнего поля перпендикулярны поверхности диэлектрика. В этом случае D в вакууме и в диэлектрике имеет одно и то же значение: D = D0..[15]

Векторы напряженности E, электрической индукции D и поляризации P связаны между собой соотношением:

Эту формулу можно получить, подставив в (·) выражения для

D и P (предлагаем сделать это самостоятельно).

Свободные и связанные заряды связаны между собой сложным образом, но для случая, когда пластина из диэлектрика вносится в однородное внешнее электрическое поле, силовые линии которого перпендикулярны поверхности пластины, соотношение между s своб и s¢связ можно найти из (·).

	Приравнивая Е из этих формул, и умножая обе части равенства на e0, получим:
	связь поверхностной плотности связанных и свободных зарядов

Диэлектрическая проницаемость e это макрохарактеристика диэлектрика, она зависит от структуры и свойств его молекул и от температуры диэлектрика. Экспериментально определить e легко. Для этого нужно поместить диэлектрик в конденсатор и измерить емкость с диэлектриком и без него: e = С/С0. Исследуя зависимость диэлектрической проницаемости e от температуры Т, можно получить сведения о свойствах молекул. Для этого нужно иметь формулу зависимости e (Т), в которую входили бы характеристики молекул. Сложность в получении такой формулы состоит в том, что средняя напряженность поля внутри диэлектрика и поля, окружающего данную молекулу, отличаются друг от друга. Разными учеными теоретически были получены различные формулы. Наиболее универсальной формулой является:

где n – концентрация молекул, a — поляризуемость молекулы, р0 — дипольный момент молекулы, k – постоянная Больцмана, T – абсолютная температура, e0 – электрическая постояннная

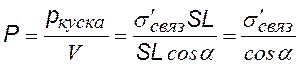
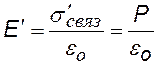
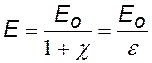
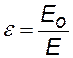
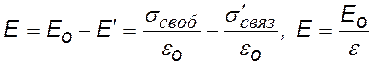
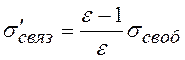
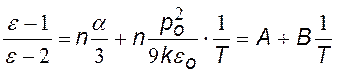
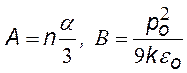
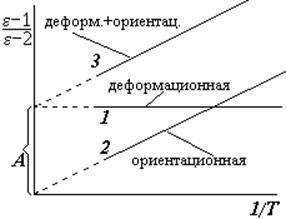Из формулы следует, что если отложить на графике величину (e — 1)/(e — 2) в зависимости от обратной температуры (1/Т) для различных диэлектриков, то можно получить прямые 1, 2 или 3 (если формула справедлива!). В случае 1 (горизонтальная прямая) мы имеем дело с диэлектриком, у которого молекулы – неполярные. Под действием внешнего поля у таких молекул возникает индуцированный момент, который не зависит от температуры. Измерив величину А, можно вычислить поляризуемость a молекулы. Случай 2 соответствует диэлектрику с ориентационной поляризацией; по наклону прямой можно вычислить собственный дипольный момент р0 молекулы. В случае 3 можно сделать вывод, что молекулы диэлектрика полярные, но под действием поля у них дополнительно возникает индуцированный дипольный момент

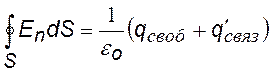Теорема Гаусса при наличии диэлектрика.

Пусть заряд +q окружен оболочкой из твердого диэлектрика. На рисунке показаны схематически несколько молекул диэлектрика. Они стремятся ориентироваться по полю этого заряда. Диэлектрик поляризуется, на внешней его поверхности возникает связанный заряд +q¢связ , на внутренней —q¢связ. Допустим, мы хотим найти напряженность поля в диэлектрике с помощью теоремы Гаусса. Выбираем гауссову поверхность в виде сферы. Она будет охватывать не только заряд +q, но и отрицательные связанные заряды, как-бы «отсекая» часть молекулы.

Наташа

Автор

Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку.