Введение в механику сплошной среды
Механика сплошной среды (МСС) – раздел теоретической физики, в котором изучаются макроскопические движения твердых, жидких и газообразных сред с учетом и под влиянием физических полей различной природы. В отличие от теоретической механики, где изучается движение системы материальных точек и твердых тел, в МСС приходится оценивать не только влияние на частицы внешних факторов, но и учитывать взаимовлияние их друг с другом и отказаться от гипотезы абсолютно твердого тела. В связи с этим в круг вопросов МСС входят теории деформирования твердых тел, теории течения жидких и газообразных тел, теории, изучающие поведения тел, которые проявляют признаки и упругости и течения. Более того, здесь рассматриваются теории перехода тела из одного агрегатного состояния в другое, пластичность, поляризации, намагниченности, диффузии и другие фазовые превращения. Тем не менее, разработанные методы справедливы не для любых объектов, с которыми оперирует техника, и тем более природа. И это связано исключительно с атомно-молекулярным строением тел. Только в том случае, когда движением отдельных корпускулярных частиц, каковыми являются атомы и молекулы, можно пренебречь в общем движении их большой массы, можно говорить о законах движения механики сплошной среды. В связи с этим можно сказать, что строительные конструкции, шестерни механизмов вращения, истечение газа из сопла, обтекание жидкостью твердых тел и многое другое можно рассматривать методами МСС. А движение отдельной молекулы в замкнутом сосуде, поведение нано-трубок в электрических и магнитных полях, растяжение нано-пленок и прочие проблемы нано-мира не входят в круг задач МСС. Поэтому в основе этой науки лежит гипотеза о сплошности или непрерывности вещества, которая позволяет рассматривать все тела с непрерывно распределенной массой, отбрасывая их реальное дискретное строение. В этом случае удается весьма успешно оперировать с полями физических величин как непрерывными функциями. Каждую точку можем считать предельной точкой множества распределенных материальных точек, что, в свою очередь, позволяет использовать хорошо разработанный аппарат исчисления бесконечно малых. Исследуя поведение материальных частиц, механика сплошной среды занимает промежуточное положение между механикой, физикой твердого тела и молекулярной физикой. Это проявляется в том, что материальные частицы в механике сплошной среды, с одной стороны, подчиняются фундаментальным законам механики, но с другой стороны, они испытывают внутренние взаимодействия, которые являются прямым следствием внутреннего межмолекулярного взаимодействия. Это обстоятельство приводит к тому, что модели МСС строятся, как с использованием фундаментальных законов механики, справедливых для материальных систем микроскопических, макроскопических и мегаскопических размеров, так и других дополнительных законов межмолекулярного взаимодействия, которые имеют место лишь в определенных рамках изменения внешних параметров. Примером фундаментальных законов для твердого тела могут служить законы сохранения импульса и момента импульса, а дополнительным законом — линейный закон Гука, т. к. при больших деформациях возникает пластичность и линейность нарушается.
Уравнения, получающиеся из фундаментальных и дополнительных законов, должны обладать полнотой, в том смысле, что их вполне достаточно для получения решения, описывающего поведение рассматриваемого тела или протекающего в нем процесса. Основной задачей МСС является построение таких систем уравнений, которые и определяют соответствующую модель эволюционирующей материальной среды.
Актуальность пособия. Несмотря на то, что первые уравнения МСС были получены более двухсот лет назад, и к настоящему времени имеются учебные пособия и даже фундаментальные монографии, актуальность самой науки неуклонно возрастает. Особенно это стало заметно в связи с применением в технике активных материалов, таких, которые способны преобразовывать механическую энергию в другие виды энергии, и наоборот. В классических учебниках такие модели не описываются, а фундаментальные монографии порой трудно доступны, а порой трудны для понимания учащимися. Все это делает актуальным разработку вспомогательных учебных пособий, которые бы описывали усложненные модели, с одной стороны, и обладали свойством математической строгости и физической простоты в понимании, с другой стороны.
Цели и задачи курса. Настоящее учебное пособие имеет своими целями последовательное изучение гипотез и аксиом; фундаментальных балансных законов и вывод, вытекающих из них уравнений; принципов выбора вспомогательных законов и получающихся определяющих соотношений; описание взаимодействующих физических полей с указанием их места и роли в классических и неклассических моделях МСС. Другой целью является выработка практических навыков математического моделирования механических систем на основе изложенных принципов и законов с применением численных методов и программных средств.
Задачами пособия являются: обеспечение теоретической подготовки в области фундаментальных законов естествознания; приобретение практического опыта в правильной постановке задачи, которые необходимы при использовании современных вычислительных комплексов; тренировка способностей анализа результатов и развитие инженерной интуиции.
Пути достижения. Для достижения поставленных задач необходимо последовательно изучить основы тензорного анализа, основы механики сплошных сред, основы термодинамики и электродинамики. Блок предлагаемых практических задач позволит научиться ставить классические начально-краевые задачи теории упругости, гидромеханики, аэродинамики, задачи по расчету напряженно-деформированного состояния трехмерных конструкций из анизотропных и неоднородных материалов, рассчитывать температурные и электромагнитные поля в средах определенного геометрического вида.
1 ОСНОВНЫЕ ПОНЯТИЯ
1.1 ГИПОТЕЗА СПЛОШНОСТИ
Гипотеза сплошности. Под материальными объектами подразумеваются всевозможные тела, которые могут изменять как угодно свою форму. Они могут находиться в четырех агрегатных состояниях: твердом, жидком, газообразном и состоянии плазмы. МСС имеет дело с телами, которые содержат в себе огромное число корпускулярных частиц: молекул и атомов. Отличие агрегатных состояний друг от друга заключается в степени упаковки этих частиц. Например, в обычных условиях в объеме воздуха 1 см3 содержится 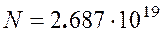 молекул, для железа
молекул, для железа 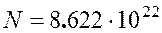 . К этому необходимо добавить, что молекулы находятся в беспрестанном движении, в газах их скорости достигают скоростей реактивных самолетов. И хотя неплотная упаковка молекул в газах позволяет молекулам иметь некоторую длину свободного пробега, все же столкновений наблюдается огромное число. В жидких телах молекулы упакованы более плотно, чем в газах, но почти не связаны друг с другом, что также позволяет им перемещаться с места на место, доказательством чего является броуновское движение. В твердых телах наблюдается плотная упаковка и обнаруживается связь между соседними молекулами, а их движение проявляется в непрестанном колебательном движении возле некоторого положения равновесия. Интенсивность их движения объясняет кинетическую природу теплоты, и степень нагрева вещества, т. е. температуру. В основе всей теории механики сплошной среды лежит гипотеза о сплошности или непрерывности вещества, благодаря которой мы отвлекаемся от корпускулярного строения вещества и считаем, что масса распределена непрерывно. Для того, чтобы оценить применимость этой гипотезы к реальным средам вводится так называемое число Кнудсена, равное отношению размера молекулы на среднюю длину ее пробега
. К этому необходимо добавить, что молекулы находятся в беспрестанном движении, в газах их скорости достигают скоростей реактивных самолетов. И хотя неплотная упаковка молекул в газах позволяет молекулам иметь некоторую длину свободного пробега, все же столкновений наблюдается огромное число. В жидких телах молекулы упакованы более плотно, чем в газах, но почти не связаны друг с другом, что также позволяет им перемещаться с места на место, доказательством чего является броуновское движение. В твердых телах наблюдается плотная упаковка и обнаруживается связь между соседними молекулами, а их движение проявляется в непрестанном колебательном движении возле некоторого положения равновесия. Интенсивность их движения объясняет кинетическую природу теплоты, и степень нагрева вещества, т. е. температуру. В основе всей теории механики сплошной среды лежит гипотеза о сплошности или непрерывности вещества, благодаря которой мы отвлекаемся от корпускулярного строения вещества и считаем, что масса распределена непрерывно. Для того, чтобы оценить применимость этой гипотезы к реальным средам вводится так называемое число Кнудсена, равное отношению размера молекулы на среднюю длину ее пробега 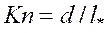 . Условно считают: если
. Условно считают: если ![]() , то среду можно рассматривать как сплошную.
, то среду можно рассматривать как сплошную.
Пример: в межзвездной среде в 1 см3 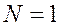 ; объемы таких сред, сравнимые по размерам с космическим кораблем, не могут изучаться методами механики сплошных сред.
; объемы таких сред, сравнимые по размерам с космическим кораблем, не могут изучаться методами механики сплошных сред.
Материальные точки. В механике, рассматриваемые материальные объекты, имеющие размеры, не играющие существенной роли в рассматриваемом процессе по отношению к размерам других объектов, принимаются за материальные точки. Любое материальное тело можно рассматривать, как состоящее из элементарных объемов, заполненных массой. И поскольку каждый элементарный объем имеет размеры, несущественные по отношению к характерному размеру всего тела, то, будучи заполнен массой (согласно гипотезе непрерывности), может рассматриваться как материальная точка, за координаты которой можно взять координаты любой геометрической точки, находящейся в этом элементарном объеме. Другими словами, под материальной частицей, находящейся в некоторой точке пространства, понимаем элемент массы, центр которого совпадает с этой точкой. Далее все тела рассматриваются в виде связанного множества материальных точек.
Понятие пространства. Будем рассматривать процессы, протекающие со скоростями значительно меньших скорости света (принимается экспериментально установленный факт, что скорость света в пустоте постоянна и одинакова во всех направлениях, независимо от скоростей источника и приемника). Под пространством будем понимать некоторое вместилище, в котором находятся материальные объекты (вопрос о том, может ли существовать пространство независимо от материальных объектов его заполняющих, здесь не рассматривается).


