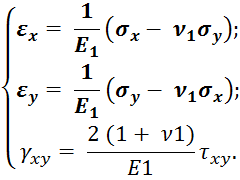Граничные условия на поверхности тела
Вопрос №9
Граничные условия на поверхности тела.
Граничные условия – условия на поверхности, ограничивающей тело. Эти условия диктуют задание или внешних поверхностных сил, или перемещений точек поверхности тела. Различают такие группы граничных условий:
1. Кинематическая – известны прогибы и углы поворота сечений:
а) сечение с нормалью ![]() :
: 
b) сечение с нормалью ![]() :
: 
2. Статическая – известны внутренние силы:
а) сечение с нормалью ![]() :
: 
b) сечение с нормалью ![]() :
: 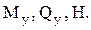
Xν=σxl+τxym+τxzn;
Yν=τyxl+σym+τyzn;
Zν=τzxl+τzym+σzn
3. Смешанная – известны часть перемещений и внутренних сил.
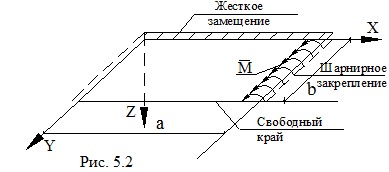
На рис. (5.2) показана срединная плоскость пластины с условиями закрепления и действующей нагрузкой. Запишем граничные условия для всех её краев:
1. При ![]()
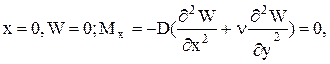 (5.8)
(5.8)
(смешанная группа).
2. При 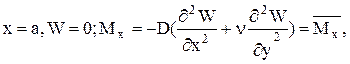 (5.9)
(5.9)
(смешанная группа).
3. При 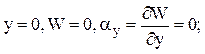 (5.10)
(5.10)
(кинематическая группа).
4. При 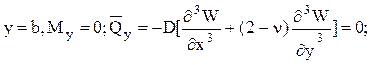 (5.11)
(5.11)
(статическая группа), где ![]() — интенсивность приведенной поперечной силы.
— интенсивность приведенной поперечной силы.
Решение задач теории упругости с данными условиями границы – единственно.
Вопрос №10
Плоское деформируемое состояние (основные гипотезы, упрощения, следующие из этих гипотез.)
В упругом теле плоская деформация возникает, если перемещения происходят только параллельно плоскости xOy:
u = u (x, y), v = v (x, y), ω = 0.
Плоское деформированное состояние, при котором деформации из плоскости, т. е. в направлении оси ![]() , равны нулю:
, равны нулю: 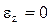 ,
, 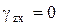 ,
, 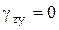 . К этой задаче относится расчет тел, вытянутых вдоль оси
. К этой задаче относится расчет тел, вытянутых вдоль оси ![]() , под действием нагрузки, перпендикулярной оси
, под действием нагрузки, перпендикулярной оси ![]() и постоянной вдоль нее. ( Например, длинные пластины, подпорные стенки, плотины).
и постоянной вдоль нее. ( Например, длинные пластины, подпорные стенки, плотины).
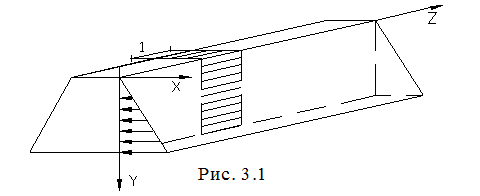
Для их расчета из тела вырезают полоску единичной ширины (рис. 3.1).
Отсутствие линейных деформаций в направлении оси Oz ведет тем не менее к появлению нормальных напряжений σz. Эти напряжения зависят от напряжений, действующих в плоскости xOy.
Из третьей формулы закона Гука при отсутствии деформации εz следует, что
εz = [σz – ν(σx + σy)]/ E = 0
откуда
σz = ν (σx + σy),
Подставляя эти соотношения в первые две формулы закона Гука, находим
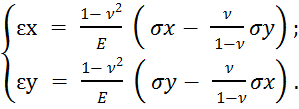
Отсюда следует, что
τyz = τzx = 0, σx = σx (x, y), σy = σy (x, y), τxy = τxy (x, y)
Основные уравнения теории упругости упрощаются следующим образом. Из дифференциальных уравнений равновесия остаются только два:
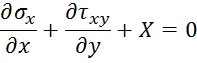
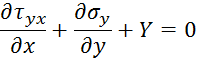
а третье обращается в тождество.
Из условий поверхности остаются тоже только два:
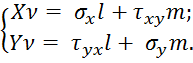
Из шести формул закона Гука остаются только три:
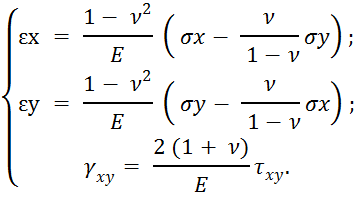
Если ввести новые упругие постоянные
E1 = E/ (1 – ν2)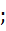
ν1 = ν/ (1 – ν),
То эти формулы примут более удобный вид: