Метрология, стандартизация и сертификация
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Метрология, стандартизация и сертификация»
Задача 1.
По величинам расчетных характеристик сопряжений деталей 1-2 и 3-5 (табл.1) выбрать в системе отверстия стандартные посадки с зазором (1-2) и с натягом (3-5). Построить поля допусков и рассчитать допуски посадок, предельные размеры и допуски сопрягаемых деталей, выполнить эскизы деталей и их соединений с простановкой точности сопрягаемых размеров.
Решение:
Посадка с зазором.
В соответствии с вариантом №73: номинальный диаметр соединения равен 63 мм, предельно допустимые эксплуатационные зазоры [![]() ]=120 мкм, [
]=120 мкм, [![]() ]=50 мкм.
]=50 мкм.
Рассчитываем допуск соединения: с зазором 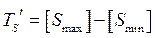 = 120 – 50 =70 (мкм).
= 120 – 50 =70 (мкм).
Рассчитываем допуски сопрягаемых деталей, исходя из условия, что детали выполнены с одинаковой точностью и 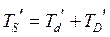 ,
, 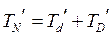 , по формуле
, по формуле 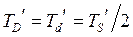 = 70/2 = 35 (мкм).
= 70/2 = 35 (мкм).
Устанавливаем номер квалитета по стандартному допуску, ближайшему к расчитанному (табл.1.8, с.43) /1/.
Квалитет 7-й, допуск по которому для размера 63 мм равен 30 мкм.
Для интервала номинальных размеров свыше 50 до 80 мм в посадке 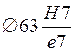 предельные зазоры равны:
предельные зазоры равны:
Smax = 120 мкм, Smin = 60 мкм (табл.1.47) /1/.
Определяем предельные отклонения сопрягаемых деталей по табл. 1.27 и 1.28 /1/:
Для отверстия ![]() H7 ES=+30 мкм, EI=0;
H7 ES=+30 мкм, EI=0;
для вала ![]() e7 es=-60 мкм, ei=-90 мкм.
e7 es=-60 мкм, ei=-90 мкм.
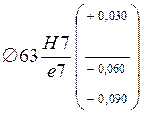
Рассчитываем предельные характеристики посадки по выбранным предельным отклонениям сопрягаемых деталей:
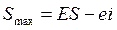 =30 – (-90) = 120 (мкм)
=30 – (-90) = 120 (мкм)
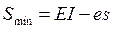 = 0 – (-60) = 60 (мкм)
= 0 – (-60) = 60 (мкм)
Проверяем выполнение неравенств для посадки с зазором:
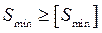 : 60 мкм> 50 мкм
: 60 мкм> 50 мкм
![]() : 120 мкм = 120 мкм/
: 120 мкм = 120 мкм/
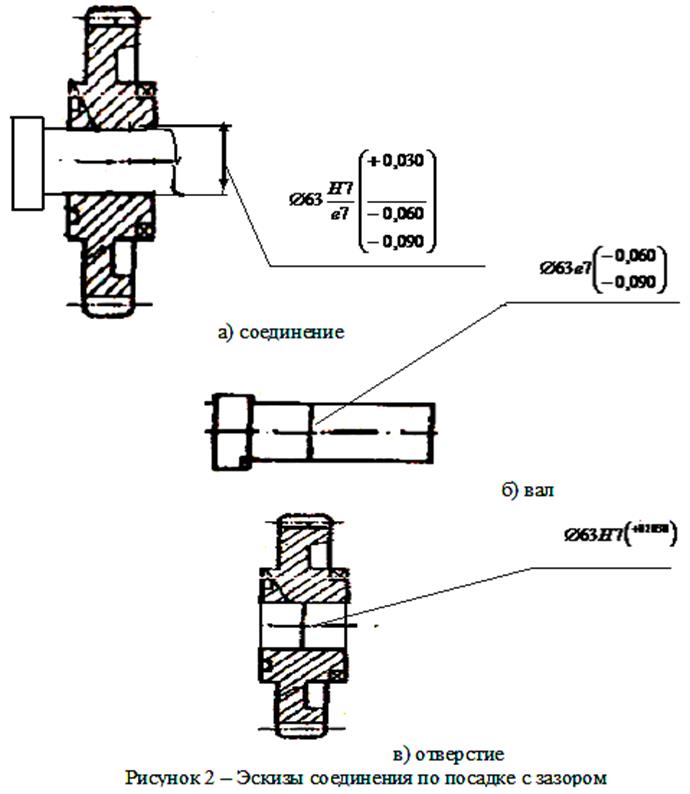
Строим схемы расположения полей допусков сопрягаемых деталей в выбранной посадке, как показано на рисунке 1.
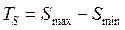 = 120 – 60 = 60 (мкм)
= 120 – 60 = 60 (мкм)
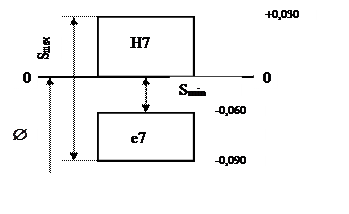 |
Рисунок 1 – Схема посадки с зазором
Рассчитываем предельные размеры и допуски сопрягаемых деталей.
Предельные размеры отверстия:
— наибольший предельный размер
Dmax = D + ES = 63 + 0,030= 63,030 (мм);
— наименьший предельный размер
Dmin = D + EI = 63 + 0= 63 (мм).
Предельные размеры вала, соответственно:
dmax = d + es = 63 + (-0,060)= 62,940 (мм);
dmin = d +ei = 63 + (-0,090)= 62,910 (мм).
Допуски сопрягаемых деталей:
Отверстия TD = Dmax – Dmin = ES – EI = 63,030 – 63 =0,030 (мм);
вала Td = dmax – dmin = es – ei = 62,940 – 62,910=0,030 (мм).
Рассчитываем допуск посадки с зазором
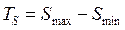 = 120 – 60 = 60 (мкм);
= 120 – 60 = 60 (мкм);
по другой формуле
TS = TD + Td = 0,030+0,030= 0,060 (мм) = 60 (мкм).
Посадка с натягом.
В соответствии с вариантом № 73 для посадки с натягом исходные данные: номинальный диаметр 180 мм, предельно допустимым эксплуатационным натягам [![]() ]=120 мкм. [
]=120 мкм. [![]() ]=40 мкм.
]=40 мкм.
Рассчитываем допуск соединения с натягом:
![]() = 120 – 40 = 80 (мкм)
= 120 – 40 = 80 (мкм)
Рассчитываем допуски сопрягаемых деталей, исходя из условия, что детали выполнены с одинаковой точностью и 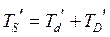 ,
, 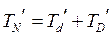 , по формуле
, по формуле 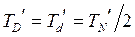 = 80/2 = 40 (мкм).
= 80/2 = 40 (мкм).
Для интервала номинальных размеров свыше 160 до 180 мм в посадке 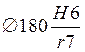 определяем предельные отклонения сопрягаемых деталей по табл. 1.27 и 1.30 /1/:
определяем предельные отклонения сопрягаемых деталей по табл. 1.27 и 1.30 /1/:
Для отверстия 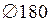 H7 ES=+25 мкм, EI=0;
H7 ES=+25 мкм, EI=0;
для вала 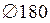 r7 es=108 мкм, ei=68 мкм.
r7 es=108 мкм, ei=68 мкм.
Предельные натяги равны:
Nmax = dmax – Dmin = es – EI = 0,108 – 0 = 0,108 (мм)= 108 (мкм),
Nmin = dmin – Dmax = ei – ES = 0,068 – 0,025 = 0,043 (мм) = 43 (мкм).
Проверяем выполнение неравенства для посадки с натягом
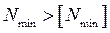 : 43 мкм>40 мкм;
: 43 мкм>40 мкм;
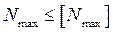 : 108 мкм <120 мкм.
: 108 мкм <120 мкм.
Обозначение посадки 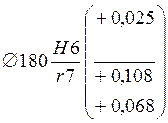 .
.
Строим схему посадки с натягом (рисунок 2).
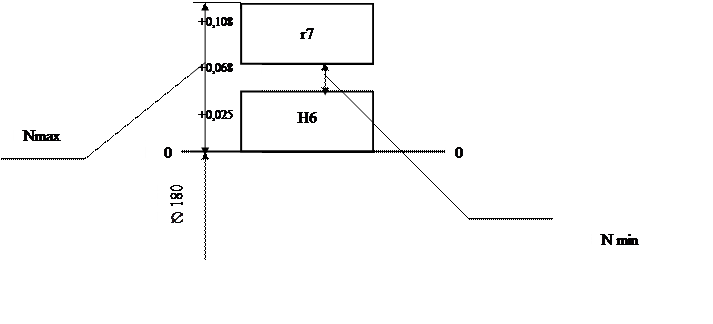 |
Рисунок 3 – Схема посадки с натягом
Предельные размеры отверстия:
— наибольший предельный размер
Dmax = D + ES = 180 + 0,025= 180,025 (мм);
— наименьший предельный размер
Dmin = D + EI = 180 + 0= 180 (мм).
Предельные размеры вала, соответственно:
dmax = d + es = 180 + 0,108= 180,108 (мм);
dmin = d +ei = 180 + 0,068= 180,068 (мм).
Допуски сопрягаемых деталей:
Отверстия TD = Dmax – Dmin = ES – EI = 0,025 – 0=0,025 (мм);
вала Td = dmax – dmin = es – ei = 0,108 – 0,068=0,040 (мм).
Допуск посадки с натягом
TN = Nmax – Nmin = 0,108 — 0,043 = 0,065 (мм)
Или по другой формуле TN = TD + Td = 0,025 + 0,0401 = 0,065 (мм).
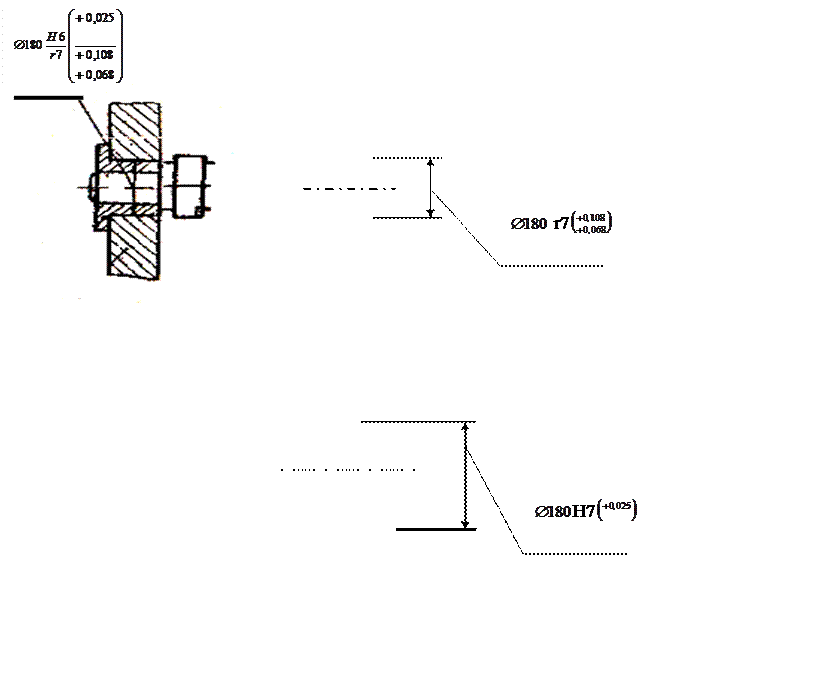 |
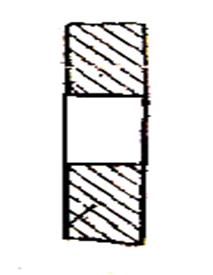 б) отверстие
б) отверстие
а) соединение;
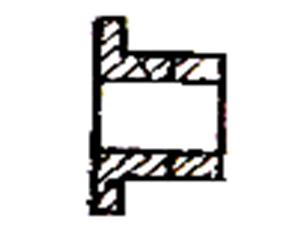
Рисунок 4 – Эскизы соединения по посадке с натягом
Задача 2.
Для указанной переходной посадки (табл.2) деталей 1 и 4 (см. рис.1) построить схему полей допусков, рассчитать характеристики посадки, предельные размеры и допуски деталей, вероятности зазора и натяга. Определить условия целесообразного использования данной посадки. Выполнить эскизы деталей и их соединения с простановкой точности сопрягаемых размеров.
Решение:
В соответствии с вариантом №73 поле допуска отверстия — H6, поле допуска вала – k5, номинальный диаметр равен 80 мм.
Определяем предельные отклонения деталей, сопрягаемых по посадке с зазором 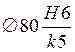 .
.
Для отверстия ![]() H6 ES=+19 мкм, EI=0;
H6 ES=+19 мкм, EI=0;
для вала ![]() k5 es=+15, ei=+2 мкм.
k5 es=+15, ei=+2 мкм.
Обозначение посадки 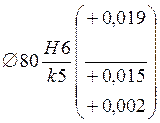 .
.
|
Строим схему переходной посадки (рисунок 3).
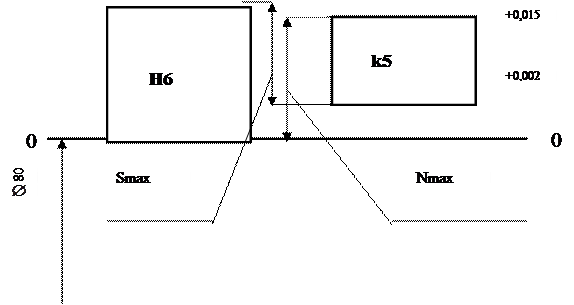 |
Рисунок 5 – Схема переходной посадки
Определяем характеристики переходной посадки, предельные размеры и допуски деталей.
Предельные размеры отверстия:
— наибольший предельный размер
Dmax = D + ES = 80 + 0,019= 80,019 (мм);
— наименьший предельный размер
Dmin = D + EI = 80 + 0= 80 (мм).
Предельные размеры вала, соответственно:
dmax = d + es = 80 + 0,015= 80,015 (мм);
dmin = d +ei = 80 + 0,002= 80,002 (мм).
Допуски сопрягаемых деталей:
Отверстия TD = Dmax – Dmin = ES – EI = 0,019 – 0=0,019 (мм);
вала Td = dmax – dmin = es – ei = 0,015 – 0,002=0,013 (мм).
Рассчитываются основные характеристики переходной посадки:
— наибольший предельный зазор
Smax = — Nmin = Dmax – dmin = ES – ei = 0,019– 0,002= 0,017 (мм);
— наибольший предельный натяг
Nmax = dmax – Dmin = es – EI = 0,015 – 0 = 0,015 (мм);
средний натяг
Nср =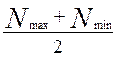 =
=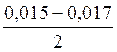 = -0,001 (мм)
= -0,001 (мм)
— допуск переходной посадки
TS, N = Smax + Nmax = 0,017 + 0,015 = 0,032 (мм);
по другой формуле
TS = TD + Td = 0,019+0,013= 0,032 (мм).
Рассчитываются вероятности получения зазоров и натягов в переходной посадке. Для этого вычисляются среднее квадратическое отклонение натяга (зазора):
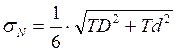 =
= 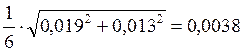 (мм)
(мм)
Определяется предел интегрирования:
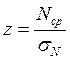 =
= 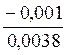 =-0,263
=-0,263
Определяется значение функции Лапласа Ф(z) = -0,1042
Рассчитывается вероятность зазора и вероятность натяга.
Вероятность зазора 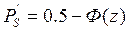 = 0,5 – (-0,1042) = 0,6042;
= 0,5 – (-0,1042) = 0,6042;
вероятность натяга 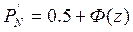 = 0,5 + (-0,1042) = 0,3958.
= 0,5 + (-0,1042) = 0,3958.
Определяются проценты зазоров и натягов:
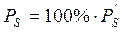 = 0,6042·100%=60,42%;
= 0,6042·100%=60,42%;
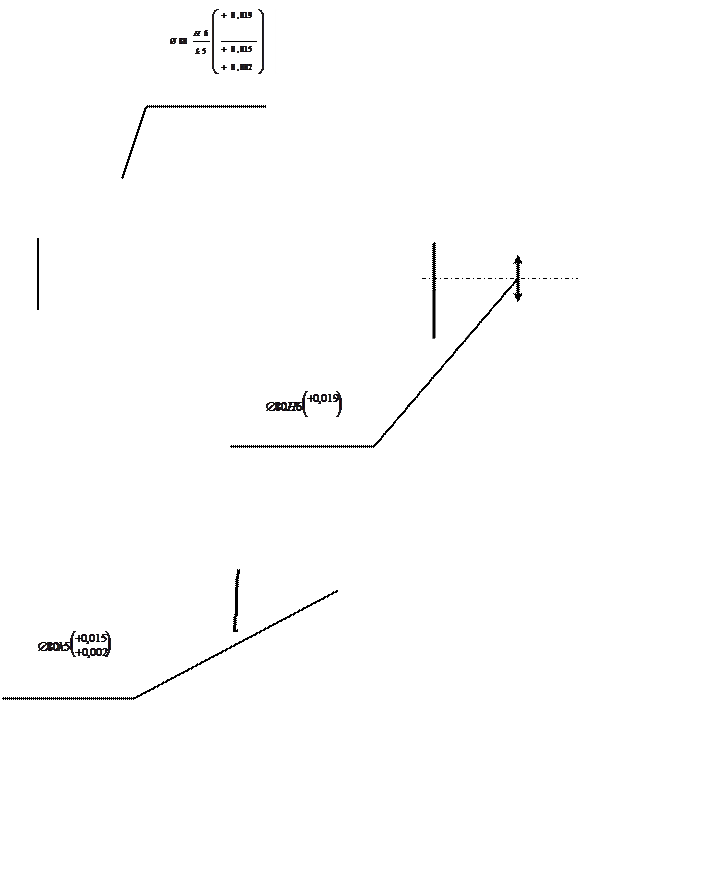
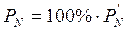 = 0,3958·100%=39,58%.
= 0,3958·100%=39,58%.
а) соединение
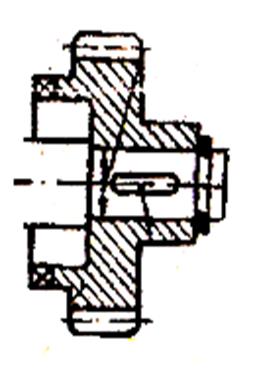
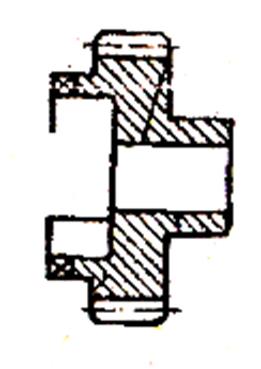
б) отверстие
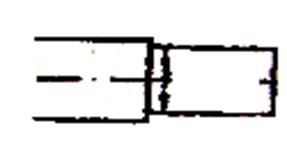
в) вал
в) вал
Рисунок 6 – Эскизы соединения по переходной посадке
Задача 3.
Произведены прямые многократные измерения электрического сопротивления, Ом. Результаты измерений в виде отклонений от номинального значения распределились по интервалам, как приведено в таблице 1.
Таблица 1 – Результаты измерений электрического сопротивления
|
Номер интервала |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Границы интервала, Ом |
-5;-4 |
-4;-3 |
-3;-2 |
-2;-1 |
-1;0 |
0;1 |
1;2 |
2;3 |
3;4 |
4;5 |
|
Количество результатов измерений, попавших в интервал |
5 |
32 |
50 |
92 |
110 |
89 |
47 |
25 |
12 |
7 |
Требуется:
а) построить гистограмму эмпирического распределения;
б) аппроксимировать эмпирическое распределение с помощью нормального закона;
в) проверить согласованность теоретического нормального и эмпирического распределений, пользуясь критерием согласия c2, при доверительной вероятности P=0,95;
г) представить результат измерений в форме доверительного интервала при заданной доверительной вероятности Р.
Решение:
1. Строим гистограмму.
Определяем относительную частоту попадания случайной величины в каждый i-тый интервал poi= mi/n,
где n – общее число экспериментальных данных и равно n=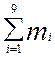 .
.
n=5+32+50+92+110+89+47+25+12+7=469
Относительные частоты по интервалам:
|
0,010661 |
0,06823 |
0,10661 |
0,196162 |
0,234542 |
0,189765 |
0,100213 |
0,053305 |
0,025586 |
0,014925373 |
po1=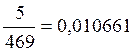
po2=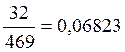
po3=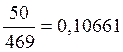
po4=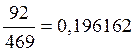
po5=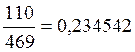
po6=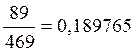
po7=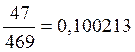
po8=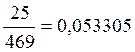
po9=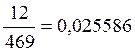
pо10=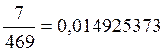
Вычисляем размах колебаний измеренной величины:
R=xmax – xmin,
где xmax, xmin — крайние значения вариационного ряда.
R= 5 – (-5) = 10 (Ом).
Рассчитываем ширину интервала:
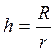
![]() ,
,
где r – число интервалов r=10.
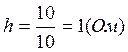 .
.
Рассчитываем для каждого интервала значения:
p’oi= mi/(n·h),
на основании которых будем строить гистограмму.
p’o1=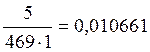
p’o2=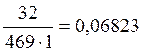
p’o3=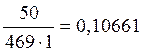
p’o4=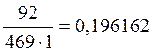
p’o5=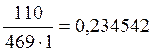
p’o6=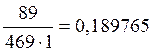
p’o7=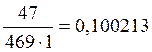
p’o8=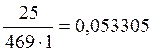
p’o9=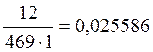
p’o10=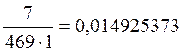
1.5. Строим гистограмму, которая представляет собой ступенчатую фигуру, состоящую из прямоугольников. Для этого по оси абсцисс откладываем отрезки, изображающие интервалы вариационного ряда, а по оси ординат – относительные частоты в интервалах, деленные на ширину интервала, как показано на рисунке 1.
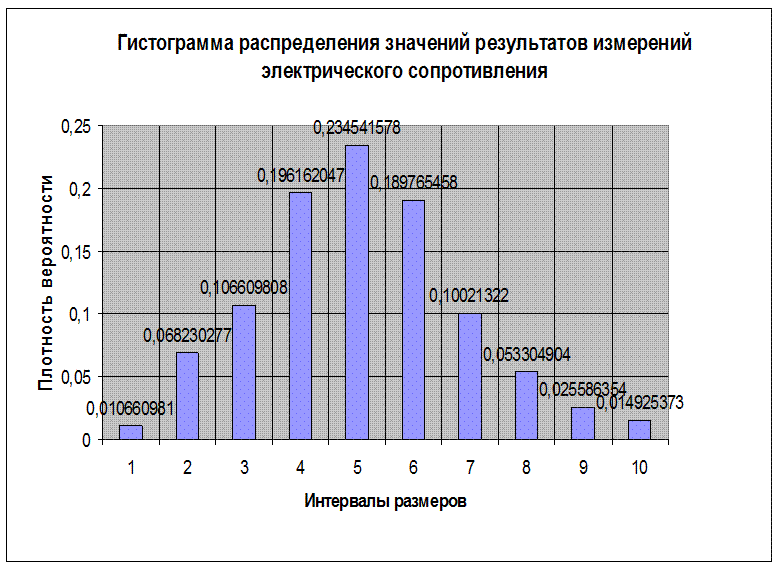
Рисунок 1 – Гистограмма результатов измерений
электрического сопротивления
2. Строим аппроксимирующую кривую, соответствующую нормальному закону распределения вероятностей.
2.1. Рассчитываем среднее арифметическое значение результатов измерений:
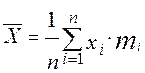 ,
,
где xi – середина i-го интервала.
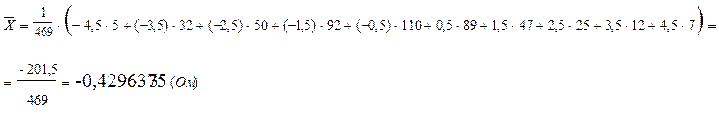 2.2. Рассчитываем СКО результатов измерений:
2.2. Рассчитываем СКО результатов измерений:
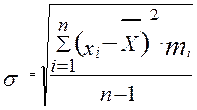 .
.
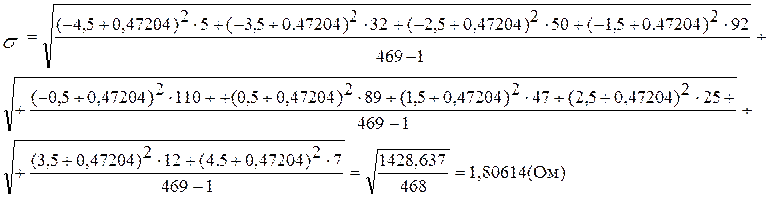
2.3. Определяем значения ординат кривой нормального распределения:
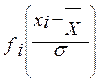 .
.
f1 = f (-4,5 +0,429637527)/1,806137 = f (-2,25363) = 0,03174
f2 = f (-3,5 +0,429637527)/1,806137 = f (-1,69996) = 0,09405
f3 = f (-2,5 +0,429637527)/1,806137 = f (-1,14629) = 0,20594
f4 = f (-1,5 +0,429637527)/1,806137= f (-0,59263) = 0,33521
f5 = f (-0,5 +0,429637527)/1,806137 = f (-0,03896) = 0,39862
f6 = f (0,5 +0,429637527)/1,806137 = f (0,51471) = 0,34849
f7 = f (1,5 +0,429637527)/1,806137 = f (1,068378) = 0,22506
f8 = f (2,5 +0,429637527)/1,806137 = f (1,622046) = 0,10741
f9 = f (3,5 +0,429637527)/1,806137 = f (2,175713) = 0,03706
f10 = f (4,5 +0,429637527)/1,806137 = f (2,729381129) = 0,00961
2.4. Вычисляем теоретическую вероятность попадания значений измеряемой величины в i-тый интервал:
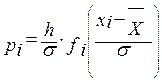
p1 = 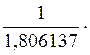 0,03174 = 0,017573
0,03174 = 0,017573
p2 = 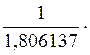 0,09405 = 0,052072
0,09405 = 0,052072
p3 = 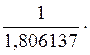 0,20594 = 0,114022
0,20594 = 0,114022
p4 = 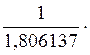 0,33521 = 0,185595
0,33521 = 0,185595
p5 = 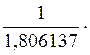 0,39862 = 0,220703
0,39862 = 0,220703
p6 = 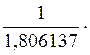 0,34849 = 0,192948
0,34849 = 0,192948
p7 = 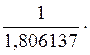 0,22506 = 0,124608
0,22506 = 0,124608
p8 = 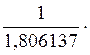 0,10741 = 0,059469
0,10741 = 0,059469
p9 = 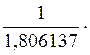 0,03706 = 0,020519
0,03706 = 0,020519
p10 = 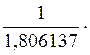 0,00961 = 0,005320747
0,00961 = 0,005320747
2.5. Проводим аппроксимирующую кривую через точки ![]() , указанные в таблице 2.
, указанные в таблице 2.
Таблица 2 – Значения ординат точек кривой нормального распределения
|
Номер интервала |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Значения ординат точек кривой |
0,017573 |
0,052072 |
0,114022 |
0,185595 |
0,220703 |
0,192948 |
0,124608 |
0,059469 |
0,020519 |
0,005320747 |
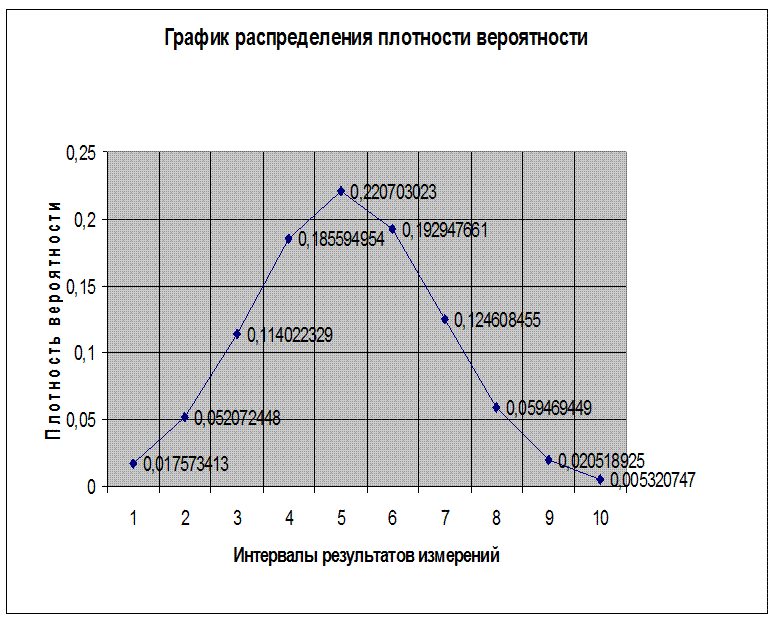
Рисунок 2 – Кривая распределения теоретической вероятности по нормальному закону
2. Проверяем согласованность теоретического и эмпирического распределений по критерию Пирсона c2.
3.1. Вычисляем показатель разности частот эмпирической и теоретической:
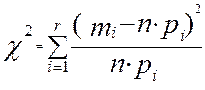 .
.
3.1.1. Вычисляем значение c2i для каждого интервала:
c21= 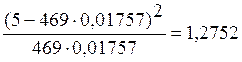
c22 = 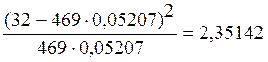
c23 = 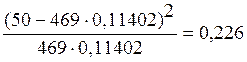
c24 = 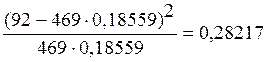
c25 = 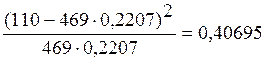
c26 = 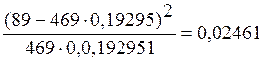
c27 = 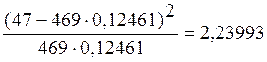
c28 = 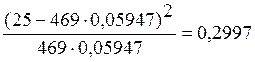
c29 = 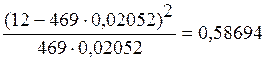
c210 = 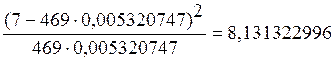
3.1.2. Рассчитываем c2:
c2 = 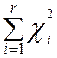 = 15,82426
= 15,82426
3.2. Определяем уровень значимости:
α = 1 – P = 1 – 0,95 = 0,05.
3.3. Рассчитываем число степеней свободы:
k = r – 3 = 10 – 3 = 7.
3.4. По таблице находим предельно допустимое значение χα2:
χα2 = 14,07.
3.5. Эмпирическое распределение не соответствует теоретическому нормальному на основании того, что не выполняется неравенство c2 < χα2 , то есть 15,82426 < 14,07. Но гипотезу о соответствии нормальному распределению можно принять для вероятности Р=0,975, для которой χα2 = 16,01.
4. Представляем результат измерений X в форме доверительного интервала:
![]() ,
,
где tp – коэффициент Стьюдента при заданной доверительной вероятности P=0,95 tp = 1,96.
![]()
-0,5931 Ом < X < -0,26617 Ом.
Список использованных источников:
1. Допуски и посадки. Справ. I т. под. ред. Мягкова В. Д. — Л.: Машиностроение, 1982.
2. Маркин Н. С. Основы теории обработки результатов измерений. — . М.: Изд-во стандартов, 1991.
3. Маркин Н. С. Практикум по метрологии. — М.: Изд-во стандартов, 1994.
4. Сергеев А. Г., Крохин В. В. Метрология, М.:«Логос», 2002.
5. Кошлякова И. Г., Ваганов В. А., Хлебунов А. Ф. Практикум по метрологии и стандартизации. Пособие к решению задач. – Изд. центр ДГТУ, 2013.


