Метрология стандартизация и сертификация 2015
Объем и требования к Семестровому заданию
1. Семестровое задание состоит из четырех задач.
2. Семестровое задание должно выполняться самостоятельно, после проработки соответствующего раздела курса по учебникам, указанным ниже.
3. Перед решением задач необходимо разобрать условие задачи и выписать цифровые данные по последней для задач №1,3 и предпоследней цифре номера зачетки для задач №2,4.
4. При оформлении Семестрового задания необходимо:
а) написать полностью условие задачи;
б) начертить графики по тексту на основании исходных и расчетных данных.
5. Семестровое задание должно быть аккуратно оформлено, написано разборчивым почерком или выполнена с помощью персонального компьютера.
6. Решение необходимо выполнить сначала в буквенном выражении, после чего подставить вместо букв числовые значения и производить вычисления. Следует указывать наименование и размерность всех определяемых величин.
7. Семестровое задание должно иметь титульный лист и быть закончено списком использованной литературы и подписана студентом.
Задача №1
Для определения коэффициента линейного расширений стали необходимо установить зависимость длины образца от температуры L=L0· ( 1 + α·T). Или удлинение образца ΔL = α·L0·T. Где L0 – длина образца при Т = 20°С; α – коэффициент линейного расширения (1/°С).
Экспериментальные результаты Ti; Li, приведенные в табл.1, отличаются от истинных координат Т, L из-за систематических и случайных погрешностей. Для аппроксимации экспериментальной линейной зависимости применить метод наименьших квадратов. Определить среднеквадратичное отклонение погрешности измерения длины и коэффициента линейного расширения.
|
Шифр |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Темп. С° |
Длина образца Li ; мм |
|||||||||
|
20 |
20,00 |
30,00 |
40,00 |
50,00 |
60,00 |
70,00 |
80,00 |
85,00 |
90,00 |
95,00 |
|
100 |
20,02 |
30,03 |
40,04 |
50,05 |
60,07 |
70,08 |
80,09 |
85,09 |
90,10 |
95,10 |
|
150 |
20,04 |
30,05 |
40,07 |
50,08 |
60,10 |
70,12 |
80,14 |
85,15 |
90,16 |
95,16 |
|
200 |
20,05 |
30,08 |
40,10 |
50,13 |
60,15 |
70,18 |
80,20 |
85,21 |
90,22 |
95,23 |
|
300 |
20,08 |
30,10 |
40,15 |
50,19 |
60,23 |
70,27 |
80,30 |
85,32 |
90,34 |
95,36 |
|
400 |
20,10 |
30,13 |
40,20 |
50,26 |
60,31 |
70,36 |
80,41 |
85,44 |
90,46 |
95,48 |
|
500 |
20,13 |
30,19 |
40,26 |
50,32 |
60,39 |
70,45 |
80,52 |
85,55 |
90,58 |
95,62 |
Перед решением задачи изучить теоретический материал по учебнику «Метрология, стандартизация и сертификация» М., Форум-Инфра-М 2007г, стр. 56 — 58.
Методические указания к решению задачи №1
Перед решением задачи необходимо изучить теоретический материал. Сущность метода заключается в том, что наивероятнейшими значениями аргументов искомой аналитической зависимости будут такие, при которых сумма квадратов отклонений экспериментальных значений функции от самой исследуемой функции будет наименьшей:
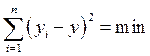
Искомая функциональная зависимость имеет линейный характер
y=a+bx
График функции представляет прямую линию с коэффициентом b=tga, пересекающая ось ординат в точке y=a
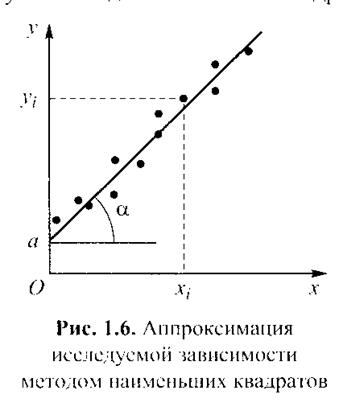
В соответствии с методом наименьших квадратов искомым постоянным соответствует минимальное значение выражения:
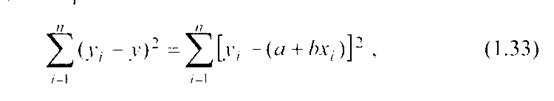
Можно показать:

В соответствии с этими формулами необходимо вычислить:
1. Постоянные коэффициенты a и b по формулам 1.34. Предварительно вычислив S1, S2, S3, S4, S5 по формулам 1.35, где xi – Ti , yi -Δ Li, n=7 – количество экспериментов.
2. Построить теоретический график зависимости приращение длины ΔL от температуры и нанести на него экспериментальные точки.
3. Вычислить среднеквадратичное отклонение погрешности измерения длины по формуле 1.37
4. Вычислить среднеквадратичное отклонение найденных значений а и b по формулам 1.36
Задача №2
Для оценки влияния случайных погрешностей на стабильность технологического процесса шлифования роликов провели 100 последовательных измерений диаметров роликов в пределах 20,00 до 20,35 мм и разбили на семь интервалов. Распределение количества роликов по интервалам (частота m) приведено в табл.2 . Вариант выбрать по последней цифре шифра. Построить гистограмму распределения измеренных диаметров. Определить среднее квадратичное отклонение измерений диаметров роликов. Построить кривую нормального распределения Гаусса, соответствующую вычисленному значению среднего квадратичного отклонения. Установить вероятность работы без брака при допуске на диаметр 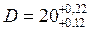 .
.
|
шифр |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Интервал, мм |
Частота, m |
|||||||||
|
20,0 – 20,05 |
2 |
1 |
1 |
3 |
2 |
3 |
1 |
1 |
1 |
1 |
|
20,5 – 20,10 |
11 |
10 |
12 |
11 |
10 |
12 |
10 |
11 |
10 |
9 |
|
20,10 – 20,15 |
19 |
20 |
19 |
21 |
20 |
21 |
20 |
21 |
22 |
22 |
|
20,15 – 20,20 |
28 |
29 |
30 |
31 |
30 |
29 |
30 |
31 |
32 |
33 |
|
20,20 – 20,25 |
22 |
21 |
20 |
20 |
22 |
21 |
23 |
22 |
21 |
22 |
|
20,25 – 20,30 |
15 |
16 |
17 |
11 |
14 |
13 |
14 |
12 |
11 |
10 |
|
20,30 – 20,35 |
3 |
3 |
1 |
3 |
2 |
1 |
2 |
2 |
3 |
3 |
|
Итого n=Σm: |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
100 |
Перед решением задачи изучить теоретический материал по учебнику Я. М. Радкевич и др. Метрология, стандартизация и сертификация. М. «Высшая школа» 2007. с. 36-66.
Методические указания по решению задачи №2
1. Построить гистограмму распределения измеренных размеров роликов, для чего по оси абсцисс отложить в масштабе размеры в соответствии с вариантом от 20,00 до 20,35 Разбить эту область на семь интервалов согласно задания (см. табл.2.). По оси ординат отложить соответствующую частоту m или частость m/n в масштабе. Последовательно соединить точки, соответствующие середине каждого интервала. Ломаная линия называется гистограммой распределения эмпирической кривой распределения.
2. Посчитать среднее взвешенное арифметическое значение действительных размеров роликов данной партии по формуле:
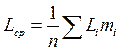
Где mi – частота (количество роликов данного интервала размеров)
n=100 – количество заготовок партии.
3. Посчитать среднее квадратическое отклонение, определяемое по формуле:
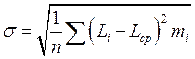
4. Кривая, характеризующая дифференциальный закон нормального распределения показан на рис. 2.9.
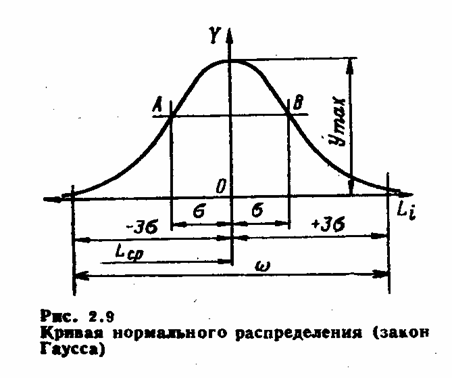
Построить кривую нормального распределения по пяти точкам для вычисленного среднего квадратического отклонения:
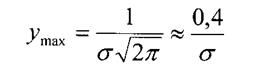
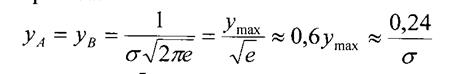
Кривая асимптотически приближается к оси абсцисс. На расстоянии ±3 y ~ 0. Фактическое поле рассеивания размеров роликов ω = 6σ
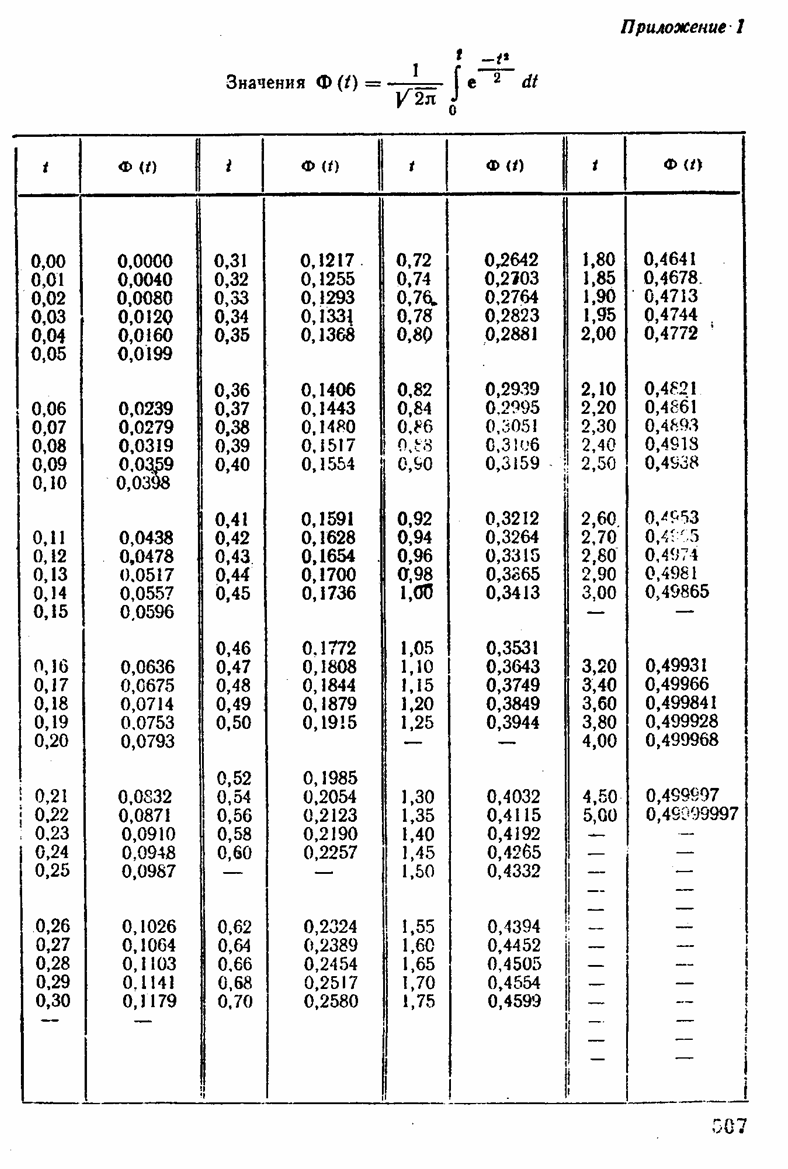
5. Вычислить число годных роликов в пределах допуска на размер. На кривую нормального распределения наносим границы поля допуска на размер роликов![]() . Площадь заштрихованных участков представляет собой количество роликов, выходящих за пределы допуска. Для определения количества роликов, входящих в допуск на размер роликов, необходимо найти площадь, ограниченную кривой и осью абсцисс на длине, равной допуску Т по формуле Лапласа см. Приложение 1:
. Площадь заштрихованных участков представляет собой количество роликов, выходящих за пределы допуска. Для определения количества роликов, входящих в допуск на размер роликов, необходимо найти площадь, ограниченную кривой и осью абсцисс на длине, равной допуску Т по формуле Лапласа см. Приложение 1:
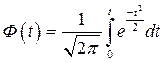
Где t = (L—Lcp)/ = xo/ при симметричном расположении поля рассеяния относительно поля допуска.
При несимметричном расположении рассчитываются значения хА и tA по площади А: хА =Т/2 +ΔН ; tA = xA/ и по Приложению 1 Ф(tA).
Затем рассчитываются хВ и tВ по площади В: хВ = Т/2- ΔН ; tB = xB/ и по Приложению 1 Ф(tB).
Общее количество роликов, входящих в допуск на размер равно сумме площадей А и В. Ф( t) = Ф(tA) + Ф(tB), дробную величину которой пересчитываем в проценты или число роликов в партии.
Задача №3
Манометр, измеряющий давление в рабочем диапазоне от рmin(мПа)до рmax(мПа), имеет граничную абсолютную погрешность Δр (мПа).Определить класс точности манометра.
|
шифр |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
рmin(мПа) |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
0,05 |
|
рmax(мПа) |
2,0 |
2,1 |
2,2 |
2,3 |
2,4 |
2,5 |
2,6 |
2,7 |
2,8 |
2,9 |
|
Δр (мПа) |
0,02 |
0,025 |
0,03 |
0,035 |
0,04 |
0,045 |
0,05 |
0,055 |
0,06 |
0,065 |
Методические указания по решению задачи №3
1. Определить приведенную погрешность манометра по формуле:
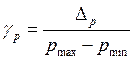
2. Выбрать класс точности манометра из стандартного ряда (1;1,5;1,6;2,0;2,5;3,0;4,0;5,0;6,0) для величины
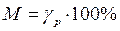
Задача №4
Определить предельные размеры, максимальные и минимальные зазоры и натяги, допуски размеров и допуски посадок для заданной посадки. Определить систему образования посадки. Результаты свести в таблицу.
|
шифр |
1 |
2 |
3 |
4 |
5 |
|
посадка |
|
|
|
|
|
|
шифр |
6 |
7 |
8 |
9 |
0 |
|
посадка |
|
|
|
|
|
Методические указания по решению задачи №4
1. Номинальный(D— отверстия,d-вала) – это размер, относительно которого определяются предельные размеры и который служит началом отсчета отклонений.
2. Наибольший предельный размер(Dmax— отверстия, dmax-вала) – это больший из двух предельных, наименьший(Dmin— отверстия, dmin-вала) — это меньший из двух предельных размеров.
3. Отклонение — это алгебраическая разность между предельным размером и номинальным размером. приняты условные обозначения: верхнее отклонение отверстия – ES, вала — es, нижнее отклонение отверстия – EI, вала ei.
Dmax=D+ES; Dmin=D+EI; dmax=d+es; dmin =d+ei
4. Допуск Т – это разность между наибольшим и наименьшим предельными размерами или абсолютная величина алгебраической разности между верхним и нижним отклонениями.
TD=Dmax-Dmin; Td=dmax-dmin.
5. Зазор S – разность размеров отверстия и вала, если размер отверстия больше размера вала. Наибольший, наименьший зазоры определяют по формулам:
![]()
6. Натяг N – разность размеров вала и отверстия до сборки, если размер вала больше размера отверстия. Наибольший, наименьший натяги определяют по формулам:
![]()
7. Допуск посадки — разность между наибольшими и наименьшими допускаемыми зазорами ( допуск зазора TS в посадках с зазором). Или наибольшим и наименьшим допускаемыми натягами ( допуск натяга TN в посадках с натягом):
![]()
8. Посадки в системе отверстия – это посадки, в которых различные зазоры и натяги получаются соединением различных валов с основным отверстием. У основного отверстия нижнее отклонение равно нулю, а основное отверстие обозначается Н. На чертеже такие посадки обозначаются: Ø50Н9/d9; Ø50Н7/r6.
Посадки в системе вала – это посадки, в которых различные зазоры и натяги получаются соединением различных отверстий с основным валом. У основного вала верхнее отклонение рано нулю, а основной вал обозначается h. На чертежах такие посадки обозначаются: Ø50D9/h9; Ø50R7/h6.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кировский вечерний факультет
Кафедра «Технология машиностроения»
СЕМЕСТРОВОЕ ЗАДАНИЕ
По дисциплине: «Метрология, стандартизация и сертификация »
По темам: «Виды и методы измерений. Случайные погрешности. Стандартизация основных норм взаимозаменяемости»
Выполнил: студент группы АЗБ-288с
Вариант
Проверил: доц., к. т.н. Егоров Н. И.
Волгоград 2015г.
Подготовил доц. к. т.н. Егоров Н. И.


