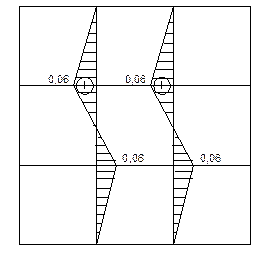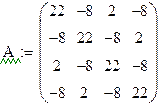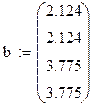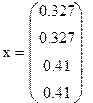Расчёт балки-стенки методом конечных разностей
Исходные данные
Задание параметров внешних воздействий и размеров пластинки берётся из методических указаний к работе. Номер схемы-3.
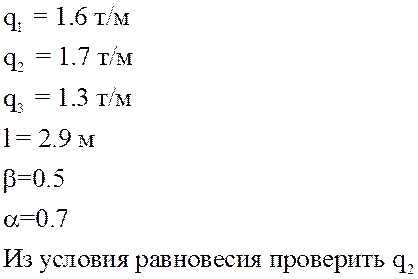

РЕШЕНИЕ
1. Проверяем равновесие системы внешних сил.
При невыполнении условия равновесия определяем нагрузку ![]()
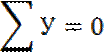
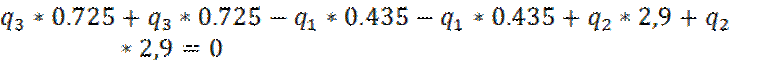
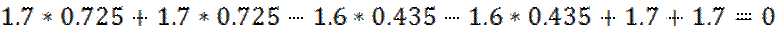
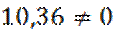
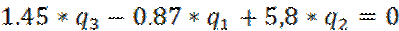
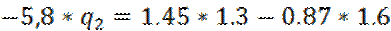
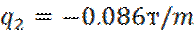
РЕШЕНИЕ
1. Разбиваем сетку с шагом 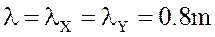
Нумерация точек приведена на рисунке 1.
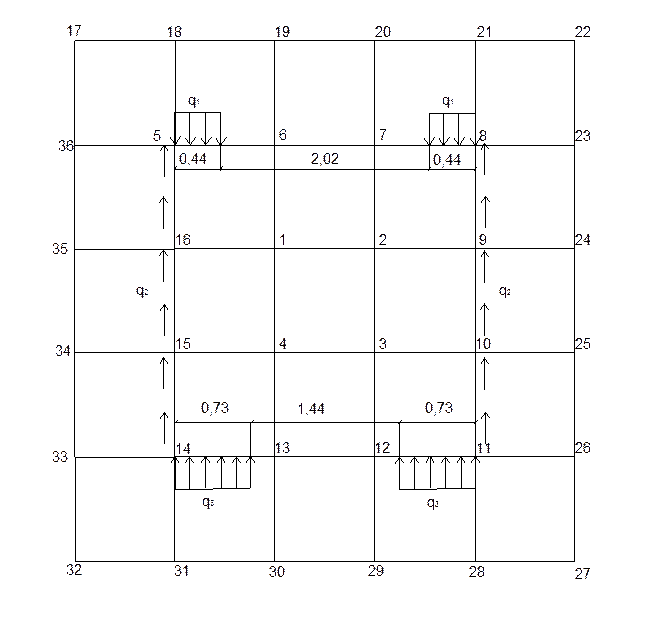
2. Рассматриваем рамный аналог и строим эпюры M, N в стержнях контура рамы

Участок 5-8
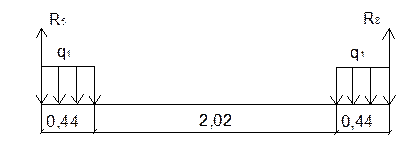
Для определения опорных реакций составим сумму моментов сил относительно точки 5,8
∑M5=0
— R8 *2.9+q1 *0.44*2.68+ q1 *0.44*0.22=0
R8 *2.9=1.87+0.15
R8 =0.7т
∑M8=0
R5 *2.9-q1 *0.44*2.68- q1 *0.44*0.22=0
R5=0.7т
∑Y=0
R5 — q1 *0.44*2+ R8 =0
0=0
Опорные реакции найдены верно.
Составим аналитические выражения для определения внутреннего усилия в точках 5,6,7,8.
0≤х≤1,44м
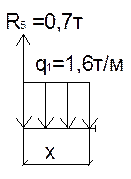 M=R5*x-q1*x2/2=0.7*x-0.8* x2
M=R5*x-q1*x2/2=0.7*x-0.8* x2
x=0 M=0
x=0.44m M=0.7*0.44-0.8*0.442=0.16тм
0≤х≤2.03м
M=R5*(0.44+x)-q1*0.44*(0.22+x)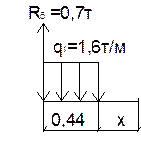 =0.16тм
=0.16тм
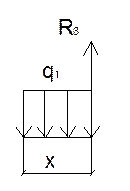
0≤х≤0.44м
M=R8*x-q1*x2/2
х=0 М=0
х=0,44м М=0,31-0,15=0,16 тм
Участок 14-11
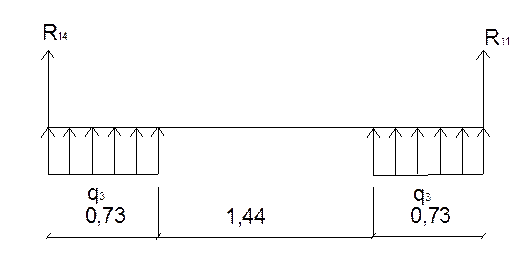
Для определения опорных реакций составим сумму моментов сил относительно точки 14
∑M14=0
— R11 *2.9-q3 *0.73*2.53- q3 *0.73*0.37=0
R11 *2.9=-2,4-0,35=-2,75
R8 =-0,95т
∑M11=0
R14 *2.9-q3 *0.73*2.53+q3 *0.73*0.37=0
—R14*2.9=2,4+0,35 R14=-0,95т
∑Y=0
—R5 + q3 *0.73*2- R8 =0
0=0
Опорные реакции найдены верно.
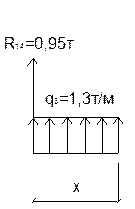
0≤х≤0.73м
M=-R14*x+q3*x2/2
х=0 М=0
х=0,73м М=-0,69+0,34=-0,35 тм
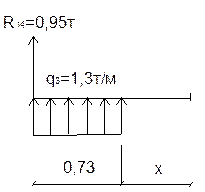
0≤х≤1,44м
M=-R14*(0,73+x)+q3*0,73*(0,37+x)=-0,35тм
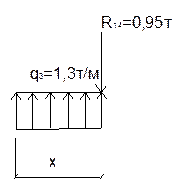
0≤х≤0.73м
M=- R11*x+q3*x2/2
х=0 М=0
х=0,73м М=-0,69+0,34=-0,35 тм
Участок 5-14
На стержень 5-14 действуют сжимающие силы R5=0.7т и R14=0,95т, нагрузка. Аналогично для участка 8-11.
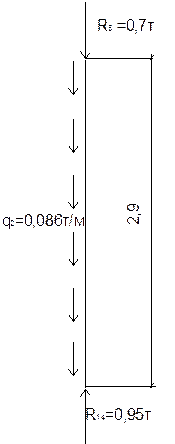
N=- q2*y—R5
y=0 N=-0.7
y=0.967m N=-0.783
y=1.934m N=-0.866
y=2.9m N=-0.95
По полученным данным построим эпюры M, N, ![]()
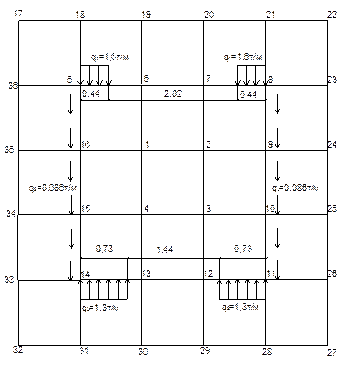
Эпюра М(тм)
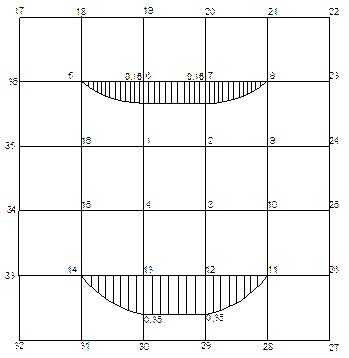
Эпюра N(т)
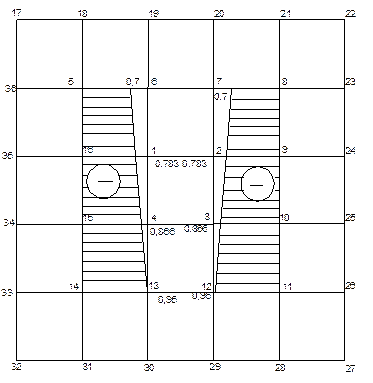
3. Определяем значения функции напряжений в контурных и законтурных точках по выражениям (1.2), (2.5).
φ 1 = φ19 =0,327; φ 2 = φ20 =0,327; φ 3 = φ29 =0,41; φ 4 = φ30 =0,41
φ5= φ8= φ9= φ10= φ11= φ14= φ15= φ16= 0
φ6=0,16; φ 7=0,16; φ12=0,35; φ13= 0,35 ;
φ24= φ2 + 2λ∙N6= φ2 +2∙0,967∙(-0,783)= φ2 -1,514
φ25= φ3 + 2λ∙N10= φ3+2∙0,967∙(-0,866)= φ3-1,675
φ34= φ4 + 2λ∙N15= φ4+2∙0,967∙(-0,866)= φ4-1,675
φ35= φ1 + 2λ∙N16= φ1+2∙0,967∙(-0,783)= φ1-1,514
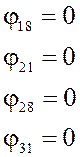
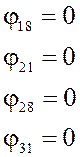
φ23= φ7 + 2λ∙N8=0,16+2∙0,967∙0,95=1,997
φ26= φ12 + 2λ∙N11=0,35+2∙0,967∙0,7=1,704
φ33= φ13 + 2λ∙N14=0,35+2∙0,967∙0,7=1,704
φ36= φ6 + 2λ∙N5=0,16+2∙0,967∙0,95=1,997
4. Составляем систему уравнений для нахождения значений функции напряжений во внутриконтурных точках:
20*φ1 -8*( φ6 + φ2 + φ4 + φ16 )+2*( φ5 + φ7+ φ3 + φ15 )+ φ19 + φ9 + φ13 + φ35 =0
20*φ2 -8*( φ1 + φ7 + φ9 + φ3 )+2*( φ6 + φ8+ φ10 + φ4 )+ φ20 + φ24 + φ12 + φ16 =0
20*φ3 -8*( φ2 + φ10 + φ4 + φ12 )+2*( φ1 + φ9+ φ11 + φ13 )+ φ7 + φ25 + φ29 + φ15 =0
20*φ4 -8*( φ1 + φ3 + φ13 + φ15 )+2*( φ2 + φ12+ φ14 + φ16 )+ φ6 + φ10 + φ30 + φ34 =0
20*φ1 -8* φ2 + 2*φ3 -8* φ4 -2,124=0
-8*φ1 +22* φ2 -8*φ3 -2* φ4 -2,124=0
2*φ1 -8* φ2 + 22*φ3 -8* φ4 -3,775=0
-8*φ1 +2* φ2 -8*φ3 +22* φ4 -3,775=0
5.Решение системы уравнений.
|
|
Матрица коэффициентов
Столбец свободных членов
|
|
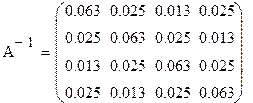
|
|
|
|
φ 1 = φ19 =0,327; φ 2 = φ20 =0,327; φ 3 = φ29 =0,41; φ 4 = φ30 =0,41
φ5= φ8= φ9= φ10= φ11= φ14= φ15= φ16= 0
φ6=0,16; φ 7=0,16; φ12=0,35; φ13= 0,35 ;
φ24= φ2 + 2λ∙N6= φ2 +2∙0,967∙(-0,783)=0,327-1,514=-1,187;
φ25= φ3 + 2λ∙N10= φ3+2∙0,967∙(-0,866)= 0,41-1,675=-1,265;
φ34= φ4 + 2λ∙N15= φ4+2∙0,967∙(-0,866)=0,41-1,675=-1,265;
φ35= φ1 + 2λ∙N16= φ1+2∙0,967∙(-0,783)= 0,327-1,514=-1,187.
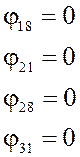
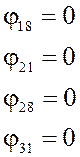
φ23= φ7 + 2λ∙N8=0,16+2∙0,967∙0,95=1,997
φ26= φ12 + 2λ∙N11=0,35+2∙0,967∙0,7=1,704
φ33= φ13 + 2λ∙N14=0,35+2∙0,967∙0,7=1,704
φ36= φ6 + 2λ∙N5=0,16+2∙0,967∙0,95=1,997
6. Определяем нормальные и касательные напряжения по выражениям (1.4), (2.2). Значения напряжений указаны в соответствии с нумерацией точек сетки.
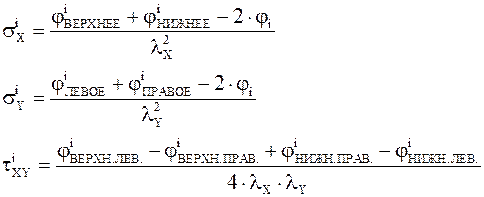
Пример расчёта:
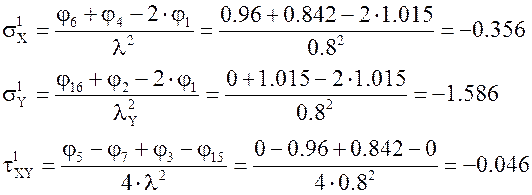
Определение σX
σХ 1= σХ 2=(φ6–2· φ1+ φ4)/λ2=(0,166-2*0,327+0,41)/0,9672=-0,083
σХ 5= σХ 8=(φ18–2· φ5+ φ16)/λ2=(0-2*0+0)/0,9672=0
σХ 6= σХ 7=(φ19–2· φ6+ φ1)/λ2=(0,327-2*0,16+0,327)/0,9672=0,357
σХ 9= σХ 16=(φ5–2· φ16+ φ15)/λ2=(0-2*0+0)/0,9672=0
σХ 4= σХ 3 =(φ1–2· φ4+ φ13)/λ2=(0,327-2*0,41+0,35)/0,9672=-0,153
σХ 3= =(φ7–2· φ4+ φ3)/λ2=(0,327-2*0,41+0,35)/0,9672=0,53
σХ 10= σХ 15=(φ16–2· φ10+ φ14)/λ2=(0-2*0+0)/0,9672=0
σХ 13= σХ 12=(φ4–2· φ13+ φ30)/λ2=(0,41-2*0,35+0,41)/0,9672=0,128
σХ 14= σХ 11=(φ15–2· φ14+ φ31)/λ2=(0-2*0+0)/0,9672=0
Определение σY
σУ 1= σУ2=(φ16–2· φ1+ φ2)/λ2=(0,166-2*0,327+0,41)/0,9672=0,06
σУ 5= σУ 8=(φ36–2· φ5+ φ6)/λ2=(1,997-2*0+0,16)/0,9672=2,308
σУ 6= σУ 7=(φ5–2· φ6+ φ7)/λ2=(0-2*0,16+0,16)/0,9672=-0,171
σУ 9= σУ 16=(φ35–2· φ16+ φ1)/λ2=(-1,187-2*0+0,327)/0,9672=-0,92
σУ 4= σУ 3=(φ15–2· φ4+ φ3)/λ2=(0-2*0,41+0,41)/0,9672=-0,06
σУ 10= σУ 15=(φ34–2· φ15+ φ4)/λ2=(-1,265-2*0+0,41)/0,9672=-0,914
σУ 13= σУ 12=(φ14–2· φ13+ φ12)/λ2=(0-2*0,35+0,35)/0,9672=-0,374
σУ 14= σУ 11=(φ33–2· φ14+ φ13)/λ2=(1,704-2*0+0,35)/0,9672=1,445
Определение τXY
τХY 5 = τХY 6 = τХY 7 = τХY 8 = τХY 11 = τХY 12 = τХY 13 = τХY 14 =0
τХY 16=- τХY9 =(φ36– φ6+ φ4– φ34)/4λ2=(1,997-0,16+0,41-1,265)/4·0,9672=0,263
τХY 1=- τХY2 =(φ5– φ7+ φ3– φ15)/4λ2=(0-0,16+0,41-0)/4·0,9672=0,067
τХY 15=- τХY10 =(φ35– φ1+ φ13– φ33)/4λ2=(-1,187-0,327+0,35-1,704)/4·0,9672=0,767
τХY 4=- τХY3 =(φ16– φ2+ φ12– φ14)/4λ2=(0-0,327+0,35-0)/4·0,9672=0,006
7. Строим эпюры нормальных и касательных напряжений балки-стенки по сетке.
Эпюра σХ, Эрюра σУ
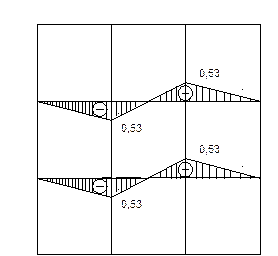
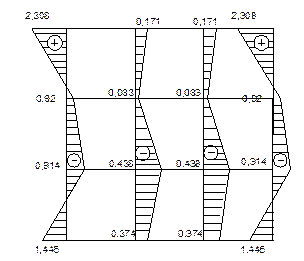
Эпюра τХY