Задача по сопромату
Е=2∙105 МПа, 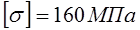
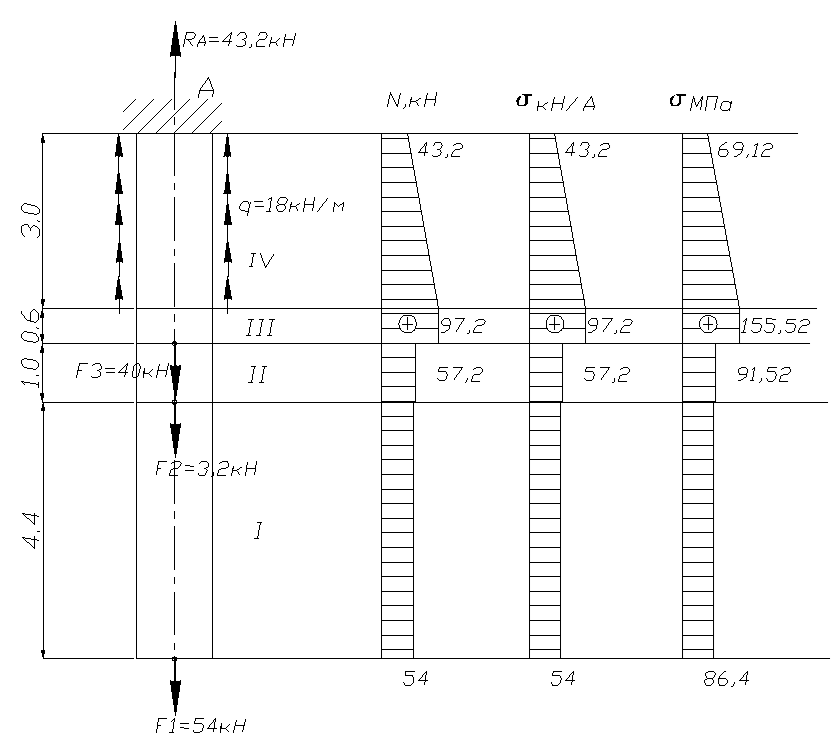
Разобьем стержень на участки нагружения, границами которых являются сечения, в которых действуют внешние сосредоточенные силы и границы приложения сосредоточенной нагрузки.
В данном случае получается 4 участка.
∑Fx=R0 +F3+F1+F2–q∙3= 0
Найдём реакцию RA в заделке:
RA = —F2—F1 –F3+q∙3=-54-3,2–40+18∙3 = -43,2 кН
Строим эпюру продольных сил N (кН)
участок I![]() NI= F1=54 кН — растяжение
NI= F1=54 кН — растяжение
участок II![]() NII= F1+F2= 54+3,2=57,2 кН — растяжение
NII= F1+F2= 54+3,2=57,2 кН — растяжение
участок III![]() NIII= F1+F2+F3=57,2+40=97,2кН – растяжение
NIII= F1+F2+F3=57,2+40=97,2кН – растяжение
участок IV![]() NIV= F1+F2+F3—q∙z4=97,2 -18∙z4=
NIV= F1+F2+F3—q∙z4=97,2 -18∙z4=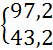 кН – растяжение
кН – растяжение
Эпюра напряжений.
Зная значения продольных сил N(z), нормальные напряжения в сечениях стержня можно определить по формуле:
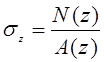
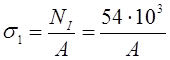
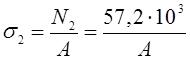
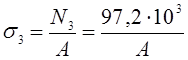
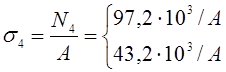
Из условия прочности определим размер квадратного поперечного сечения:
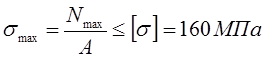
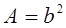
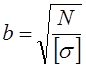
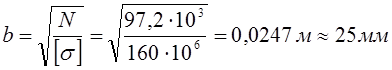
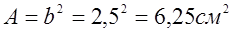
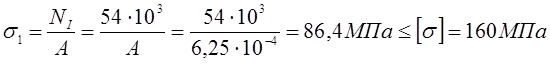
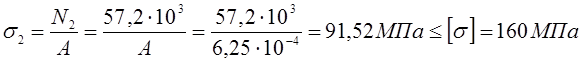
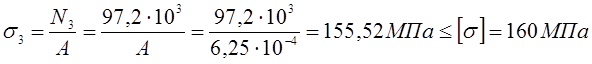
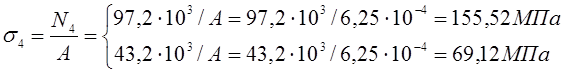
Опасное сечение на IIIучастке
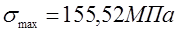
Эпюра нормальных напряжений в опасном сечении: