Акустические волны

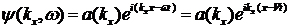. (1.24)

Волновая функция записывается следующим образом

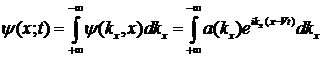. (1.25)

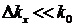Для локализованного волнового пакета функция а(кх) имеет узкий максимум при с шириной , при этом частотная ширина спектра волнового пакета 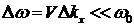(квазимонохроматическая волна)

Согласно соотношению неопределенностей, следующему из теории преобразования Фурье, ширина пространственной локализации пакета

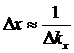. (1.26)

При расчете механического движения частицы методами классической физики часто используется сложение различных возможных движений в виде

.

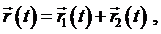
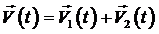Здесь и определяют i-ое состояние частицы в момент времени t, Однако эти формулы нельзя интерпретировать как принцип суперпозиции для состояний частицы, поскольку в классической физике частица не может одновременно находиться сразу в двух различных состояниях. В случае волнового движения каждый элемент линейной среды может одновременно участвовать в нескольких волновых движениях.

Лекция №2

Акустические волны

1. Закон Гука. Деформации всестороннего сжатия и сдвига. Упругие постоянные среды.

2. Акустические волны в газах, жидкостях и твёрдых телах.

3. Вывод волнового уравнения для акустических волн в стержне.

4. Основные характеристики акустических волн. Давление. Плотность энергии. Плотность потока энергии. Вектор Умова. Интенсивность.

Акустические волны переносят механические колебания макроскопических элементов среды, которые связаны между собой силами упругости. Эти силы упругости возникают в результате деформации среды. Благодаря акустическим волнам силовое воздействие, локализованное в некоторой точке тела, передаётся на все элементы тела и вызывает ускоренное движение тела как целого. Характерное время данного процесса , где — линейный размер тела и — скорость акустической волны.

При описании акустических волн обычно используется модель сплошной среды, где все физические характеристики описываются непрерывными функциями координат и не учитывается дискретное строение вещества. Любую достаточно малую локальную деформацию сплошной среды всегда можно представить в виде суммы деформаций всестороннего сжатия и сдвига, описываемых законом Гука. При выполнении закона Гука деформации являются обратимыми, а среда в отношении акустических волн является линейной. Для акустических волн выполняется принцип суперпозиции, они распространяются независимо и не взаимодействуют между собой.

В дальнейшем наше рассмотрение ограничено однородными и изотропными средами. Закон Гука проще всего сформулировать для деформаций элемента, имеющего форму кубика. В случае деформаций всестороннего сжатия, где меняется объём элемента и сохраняется его форма (рис.1), закон Гука запишется следующим образом

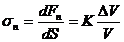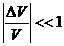, . (2.1)

Здесь — нормальное напряжение, приложенное ко всем 6 граням кубика и имеющее одинаковую величину, — нормальная компонента силы, действующая на элемент поверхности с площадью , — относительное изменение объёма V кубика и K — модуль всестороннего сжатия среды, зависящий от условий деформации.

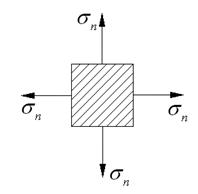
Рис.1

В случае деформации сдвига, когда меняется форма элемента при постоянном его объёме (см. рис.2, где нижняя грань кубика жестко закреплена, а боковые грани первоначально занимают вертикальное положение) закон Гука имеет вид

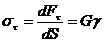, . (2.2)

Здесь – касательное напряжение, приложенное к верхней грани кубика, — касательная компонента силы, действующей на элемент поверхности с площадью , — угол сдвига (численная мера изменения формы кубика) и — модуль сдвига, зависящий от условий деформации. В газах и жидкостях модуль сдвига =0, поэтому они не обладают упругостью формы.

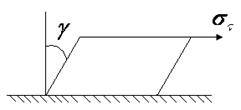
Рис.2

Если происходит растяжение или сжатие стержня вдоль его оси, то в нём одновременно происходят как деформация всестороннего стержня, так и деформация сдвига. В этом случае закон Гука, определяющий относительное изменение длины стержня под действием продольного напряжения , запишется в виде

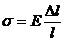. (2.3)

Здесь Е=9KG/(3K+G) — модуль Юнга материала стержня. Величина K, G и E также называются упругими постоянными среды.

Акустическая волна возникает при любом локальном силовом воздействии на среду, зависящем от времени. Особенности акустических волн определяются упругими постоянными К, G и Е среды. В газах и жидкостях, где G=0 и нет упругости формы, существуют только продольные акустические волны, в которых смещение элементов происходит в направлении распространения волны. Фазовая скорость звуковых продольных волн в газах и жидкостях описываются формулой