одномерный гармонический осциллятор

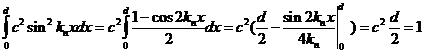(13.21)

или

. (13.22)

При вычислении интеграла (13.21) использовалось соотношение (13.18).

В случае одномерного гармонического осциллятора потенциальная энергия частицы

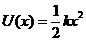, (13.23)

где k>0 – постоянная, и стационарное уравнение Шредингера принимает вид

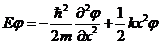. (13.24)

Уравнение (13.24) имеет ограниченные решения, удовлетворяющие граничным условиям

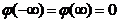, (13.25)

только для дискретных значений энергии

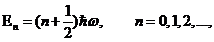(13.26)

где 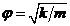— частота собственных колебаний гармонического осциллятора.

Особенность энергетического спектра гармонического осциллятора – его эквидистантность, т. е. разность энергий соседних уровней

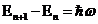(13.27)

не зависит от номера уровня n.

Энергия основного состояния гармонического осциллятора отлична от нуля и равна

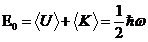, (13.28)

т. е. частица с наименьшей энергией не находится в состоянии покоя в точке x=0, как это должно быть согласно законам классической физики. Движение частицы в основном состоянии гармонического осциллятора называется нулевыми колебаниями.

Модель гармонического осциллятора широко используется для описания финитного движения линейных систем различной физической природы с потенциальной энергией типа (13.23). Метод Фурье позволяет рассматривать электромагнитное излучение как систему полевых гармонических осцилляторов с разными частотами. Энергия этих полевых гармонических осцилляторов также описывается формулой (13.26), где n – число фотонов электромагнитной волны с частотой ω.

Отсутствие фотонов не означает отсутствие электромагнитного поля, поскольку при n=0 существуют нулевые колебания поля с конечной энергией . Эти нулевые колебания электромагнитного поля представляют собой хаотические изменения во времени и пространстве векторов напряженности электрического и магнитного полей и являются составной частью физического вакуума. Они проявляют себя через взаимодействие с заряженными частицами, меняя их характеристики.

Рассмотрим стационарные состояния атома водорода, где потенциальная энергия кулоновского взаимодействия электрона с протоном имеет вид

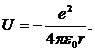(13.29)

Здесь 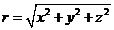— расстояние между электроном и протоном, который считается неподвижным и находящимся в начале системы координат x=y=z=0. Стационарное уравнение Шредингера (13.5) для электрона принимает вид

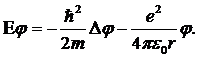(13.30)

Граничные условия формулируются следующим образом:

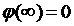, (13.31)

а в начале системы координат r=0 волновая функция имеет конечное значение. Ниже рассматриваются только те стационарные состояния атома водорода, которые соответствуют финитному движению электрона.

В классической механике при движении частицы в центральном потенциальном поле сохраняются постоянными полная механическая энергия, квадрат момента импульса относительно центра потенциального поля и проекция момента импульса на ось z перпендикулярную к плоскости орбиты частицы. Операторы, соответствующие этим динамическим величинам, коммутируют друг с другом, поэтому в стационарных состояниях атома водорода точные значения одновременно имеют:

1) энергия

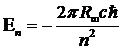, (13.32)

где n=1,2,3,… — главное квантовое, или радиальное число, — постоянная Ридберга для случая неподвижного протона, — скорость света в вакууме, = и — постоянная Планка;

2) квадрат момента импульса электрона относительно точки нахождения протона (орбитальный момент импульса)

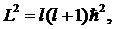(13.33)

где = 0,1,2,…, n-1 – азимутальное, или орбитальное квантовое число;

3) проекция момента импульса электрона на произвольную ось z (момент импульса электрона относительно оси z)

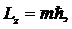(13.34)

где = 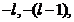…,-1,0,1,…,, — магнитное квантовое число.

Согласно формулам (13.32)-(13.34) все три величины и в стационарных состояниях квантуются, т. е. принимают только дискретные значения. Эти формулы получены путем решения стационарного уравнения Шредингера (13.30) при указанных выше граничных условиях для случая финитного движения электрона. Отметим, что выражение для энергии (13.32) совпадает с результатом теории Бора.

Набор трех квантовых чисел и полностью задает стационарное состояние атома водорода и характер движения электрона в этом состоянии. Однако энергия стационарного состояния, как видно из формулы (13.32), определяется только одним главным квантовым числом . Меняя два других квантовых числа и в рамках указанных выше ограничений, можно менять квантовое состояние т. е. движение электрона, но не его энергию. В этом случае говорят, что энергетические уровни данных квантовых состояний вырождены. Степень вырождения стационарных состояний с заданным главным квантовым числом, т. е. полное количество таких состояний с одинаковой энергией, равно (без учета спина электрона).