поперечные волны

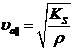, (2.4)

где ρ- плотность невозмущённой равновесной среды, — модуль адиабатного всестороннего сжатия, когда при деформации среды не учитывается теплообмен.

В твёрдых телах, где , существуют как продольные волны, распространяющиеся с фазовой скоростью

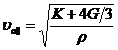, (2.5)

так и поперечные волны, распространяющиеся с фазовой скоростью

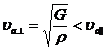. (2.6)

В поперечной волне смещения элементов происходят в плоскости, перпендикулярной к направлению распространения волны. Пространственная ориентация этих смещений в данной плоскости задаётся с помощью единичного вектора поляризации.

Если акустическая волна распространяется вдоль стержня, её фазовая скорость

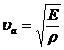. (2.7)

Деформация растяжения или сжатия вдоль стержня всегда связана с деформацией поперечного сдвига. Величина отношения относительного поперечного изменения размеров к относительному продольному изменению размера описывается коэффициентом Пуассона, численное значение которого меняется от 0 до . Отметим, что из четырёх упругих постоянных K, G, E и только две являются независимыми.

Скорость акустических волн, вообще говоря, зависит от их частоты. Данная зависимость называется дисперсией. На частоте Гц скорость акустических волн в газе при нормальных условиях близка к средней скорости теплового движения молекул и составляет несколько сотен метров в секунду (в сухом воздухе при нормальных условиях =333,45 м/с), в жидкостях-()* м/с и в твёрдых телах — ()* м/с (рекордно большая скорость звука 18* м/с наблюдается в алмазе). Для алюминия =6260 м/с, =3080 и =5000 м/с.

Если тело движется в среде со скоростью , превышающей фазовую скорость акустических волн в этой среде, то возникает ударная волна в виде скачков плотности , давления p и температуры на переднем фронте ударной волны. Передний фронт имеет форму кругового конуса с вершиной в точке нахождения тела (рис. 3). Угол полураствора конуса ударной волны описывается формулой Маха

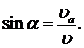
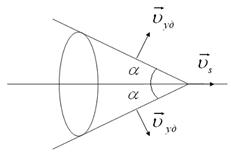
Рис.3

Скорость движения переднего фронта ударной волны превышает скорость звука в невозмущенной среде перед ударной волной.

Отметим, что при приближении скорости тела к скорости звука резко возрастает сопротивление среды, поэтому для самолётов существует проблема преодоления «звукового барьера».

По частоте акустические волны делятся на 4 группы:

1)  инфразвук < 16 Гц,

2)  звук 16 Гц < < 20 000 Гц (область слышимости для человека),

3)  ультразвук ,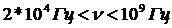

4)  гиперзвук 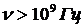(максимальная частота гиперзвука в твердых телах порядка , где – расстояние между соседними атомами, и достигает ).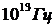

Акустические волны характеризуются с помощью непрерывных функций распределения смещения элементов среды, деформации, давления, плотности и температуры. Все эти распределения связаны между собой. Рассмотрим пример вывода волнового уравнения для продольного смещения элементов в стержне с плотностью , модулем Юнга E и площадью поперечного сечения S. Данное волновое уравнение получается путем описания ускоренного движения элемента среды с помощью законов Ньютона и Гука в условиях неоднородной деформации.

Направим ось х вдоль стержня и запишем второй закон Ньютона для элемента стержня, заключенного между сечениями х и х + dx, с учетом сил упругости

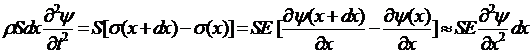(2.8)

или

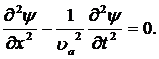(2.9)

Здесь — смещение элемента вдоль стержня относительно своего равновесного положения в точке х, — продольное напряжение в сечении х, 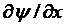— относительное изменение длины dx элемента в точке х за счет локального изменения давления и