Основные характеристики дифракции Фраунгофера

2. Основные характеристики дифракции Фраунгофера.

3. Дифракция плоской монохроматической волны на длинной прямой щели в непрозрачном плоском экране.

4. Угловое распределение интенсивности дифрагированной на щели волны в приближении Фраунгофера.

Пусть имеется скалярная монохроматическая волна

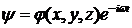, (7.1)

распространяющаяся в положительном направлении оси z. Если в некоторой плоскости z=0 задано распределение комплексной амплитуды этой волны

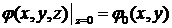, (7.2)

то распределение комплексной амплитуды в любой точке с координатами () другой плоскости z=L можно найти с помощью принципа Гюйгенса-Френеля:

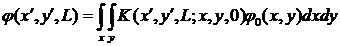. (7.3)

Здесь функция описывает в точке 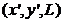вклад вторичной волны, приходящей в эту точку от вспомогательного источника с координатами (x, y,0). Координатные оси и лежат в плоскости z=L параллельно соответствующим координатным осям х и y в плоскости z=0 и имеют такие же направления, а их начало находится на оси z.

В зависимости от величины волнового параметра

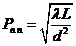(7.4)

обычно выделяют три приближения в вычислении интеграла (7.3). Здесь λ — длина волны и d – характерный размер объекта в плоскости z=0, на котором происходит дифракция. Это линейный размер освещаемого отверстия в непрозрачном экране или непрозрачного предмета на пути распространения волны.

1) Приближение геометрической оптики справедливо для случая Рв<<1, когда

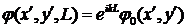. (7.5)

В этой области наблюдения, где 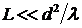, справедливы законы геометрической оптики, когда лучи света распространяются прямолинейно и дифракции нет. Поперечное распределение комплексной амплитуды сохраняется постоянным и меняется только фазовый множитель, описывающий набег фазы волны при прохождении расстояния L между плоскостями, равный . Здесь 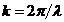— волновое число. По сути дела распределение волнового поля в плоскости z=L, поскольку величина 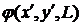определяется только значением только в одной точке с координатами , .

2) Приближение Френеля соответствует условиям наблюдения, где Рв. п.≈1, L./d>>1 и

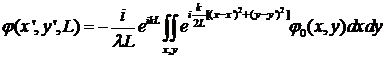. (7.6)

Данное выражение представляет собой интегральное преобразование исходного волнового поля 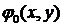и описывает дифракцию Френеля, в которой учитывается кривизна (зависимость от поперечных координат) волновой поверхности вторичных волн. В результате при распространении волны на рассматриваемое расстояние необходимо учитывать изменение поперечного распределения волнового поля. При этом величина 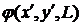определяется значениями 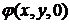в некоторой окрестности точки , и размерами .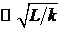

3) Приближение Фраунгофера, справедливое в дальней волновой зоне, где Рв. п.>>1 и 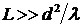, описывается выражением

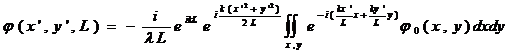. (7.7)

Это интегральное преобразование, описывающее дифракцию Фраунгофера, есть преобразование Фурье для переменных (x, y) и 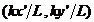. При выполнении условия 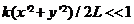комплексная амплитуда 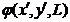с точностью до постоянного множителя является Фурье – образом комплексной амплитуды 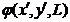. В этом случае величина в каждой точке зависит от всего распределения волнового поля .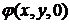

В выражении (7.7) суммируются вклады вторичных плоских волн

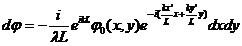, (7.8)

которые для фиксированной точки наблюдения () в плоскости z=L имеют одинаковый волновой вектор

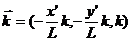, (7.9)

т. е. распространяются в одном направлении. Здесь предполагается, что .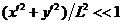

В связи с этим говорят, что дифракция Фраунгофера есть дифракция в параллельных лучах. Для наблюдения распределения интенсивности такой дифрагированной волны используется собирающая линза, которая фокусирует все параллельные лучи в одну точку своей фокальной плоскости. Роль такой собирающей линзы может выполнять глаз человека.

Таким образом, в дальней зоне дифракции участок сферической волновой поверхности вторичной волны можно с достаточной точностью заменить участком плоской волновой поверхности, если линейные размеры этого участка малы. При этом вторичные лучи, приходящие в точку наблюдения от разных вспомогательных источников, можно с той же точностью считать параллельными.

Естественное двумерное преобразование Фурье (7.7) поперечного распределения волнового поля, осуществляемое при свободном распространении монохроматической волны (7.1) между двумя параллельными плоскостями, используется в специализированных оптических компьютерах для обработки информации, записанной на световой волне. Время выполнения такого преобразования Фурье равно времени распространения света между двумя плоскостями. Исходное поперечное распределение волнового поля в плоскости z=0 задается с помощью транспаранта, коэффициент пропускания которого Т(x, y) зависит нужным образом от координат x и y. При освещении транспаранта плоской монохроматической волной на его выходной поверхности формируется необходимое распределение Т(x, y)A=φ0(x, y) волнового поля. Здесь А — амплитуда падающей на транспарант плоской волны. Вычисления на основе реально протекающих физических процессов называются имитационными. В рассматриваемом случае свободное распространение волны осуществляет вычисление образа Фурье (7.7) заданного пространственного распределения волнового поля.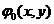

Рассмотрим дифракцию Фраунгофера для случая нормального падения плоской монохроматической волны

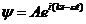(7.10)

на плоский непрозрачный экран, расположенный в плоскости z=0. В экране параллельно и симметрично относительно оси у прорезана длинная прямая щель шириной b>>λ (рис.7.1). Наблюдение ведётся в дальней волновой зоне, где справедливо приближение Фраунгофера.

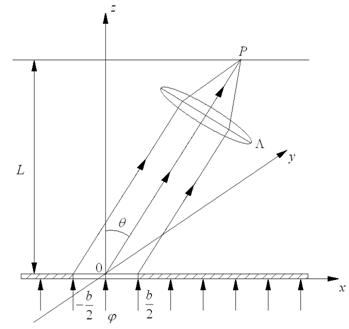
Рис.7.1

Плоскость наблюдения соответствует z=L. Параллельные дифрагированные лучи с помощью собирающей линзы фокусируются в точку Р фокальной плоскости линзы. Точка P задается с помощью угла , отсчитываемого от оси z (при , а при ).

Рассматриваемая задача дифракции имеет плоскость симметрии yoz, поэтому все элементарные вспомогательные источники на поверхности щели удобно сгруппировать в зоны в виде полосок бесконечно малой шириной dx, параллельных щели, т. е. оси у. Каждая такая полоска является источником цилиндрической вторичной волны, которую в небольшой области около точки наблюдения можно считать плоской волной и записать её комплексную амплитуд в точке P следующим образом

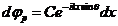, (7.11)

где С — постоянная для всех полосок, зависящая от амплитуды А падающей волны (1.10) и расстояния L, но не зависящая от координаты x рассматриваемой полоски. Вторичные волны, приходящие в точку наблюдения, отличаются только набегом фазы, обусловленным разностью хода данных волн от их вспомогательных источников до точки наблюдения. Здесь разность фаз отсчитывается от фазы вторичной волны, приходящей от центральной полоски x=0.

Согласно принципу суперпозиции полное волновое поле

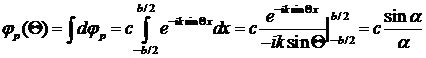, (7.12)

где 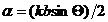и была использована формула Эйлера

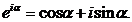
Отметим, что в силу симметрии задачи распределение поля дифрагированной волны не зависит от координаты y.

Интенсивность дифрагированной волны, пропорциональная , описывается формулой

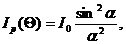(7.13)

где 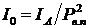-максимальная интенсивность, наблюдаемая при 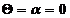, – интенсивность плоской волны с амплитудой А, падающей на экран с щелью, 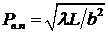– волновой параметр. Здесь учтено, что

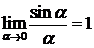
и максимум функции равен 1. График зависимости этой интенсивности от параметра приведён на рис.7.2. Распределение интенсивности симметрично относительно θ=0, поскольку .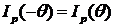

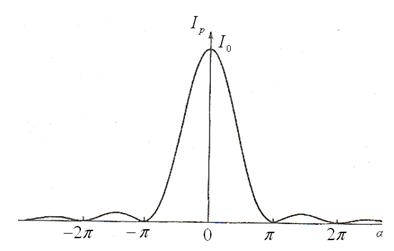
Рис.7.2

Минимальная интенсивность наблюдается при углах, удовлетворяющих уравнению

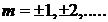, . (7.14)

Если величина угла Θ, измеренная в радианах, удовлетворяет условию 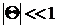, то 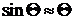, уравнение (7.14) упрощается и принимает вид

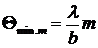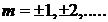, . (7.15)

Максимумы интенсивности приходятся на углы, лежащие примерно посередине между двумя углами и 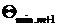, определяющими два соседних минимума (7.15). Центральный дифракционный максимум с интенсивностью наблюдается при

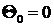, (7.16)

а все побочные максимумы соответствуют углам наблюдения

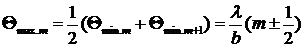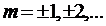, , (7.17)

где знак «+» берется для ,а знак «-» – для Интенсивность побочных максимумов быстро убывает с ростом величины :

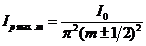. (7.18)

Полная мощность N излучения, прошедшего через щель шириной b и единичной длины, описывается формулой

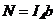, (7.19)