ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
Рассмотренные выше магнитные явления были исследованы в 1820-1821 годах. Затем ученые задались вопросом, если электрический ток создает магнитное поле, то не может ли магнитное поле создавать электрический ток? Десять лет спустя Майкл Фарадей (1791-1867) обнаружил этот эффект[1].
4.1. Опыты Фарадея. ЭДС индукции
|
а б Рис. 4.1. Схемы опытов Фарадея |
В 1831г. Фарадей открыл явление электромагнитной индукции, заключающееся в возникновении тока под действием переменного магнитного поля. Схема опытов Фарадея приведена на рис. 4.1. Он установил, что ток в первой катушке возникает: при движении постоянного магнита относительно катушки (рис.4.1а); при изменении тока во второй катушке (рис.4.1б); при движении катушек относительно друг друга (во второй при этом существует постоянный ток). Чем быстрее движется магнит или вторая катушка, тем больше сила тока. Отсюда можно было сделать вывод: в замкнутом контуре возникает ток при изменении потока магнитной индукции, пронизывающего контур. Это означает, что в контуре возникает ЭДС индукции:
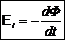 . (4.1)
. (4.1)
ЭДС индукции равна скорости изменения магнитного потока, пронизывающего контур (точнее, производной от потока по времени). Если в контуре имеется N витков с плотной намоткой, то индуцированные в каждом витке ЭДС будут складываться, и формула (4.1) принимает вид:
![]() . (4.2)
. (4.2)
|
Рис.4.2. Демонстрация правила Ленца |
Знак (-) в правой части формул отражает правило Ленца: возникающий в замкнутом контуре ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван (т. е. противодействует причине, его породившей). На рис. 4.2 показан опыт с внесением магнита в замкнутое кольцо. Возникающий в кольце индукционный ток создает магнитное поле, препятствующее внесению магнита, и отталкивает кольцо от магнита. При внесении магнита в разрезанное кольцо эффект отсутствует.
Посмотрим, что происходило бы, если бы правило Ленца не выполнялось. Индукционный ток в этой ситуации создавал бы магнитный поток, направление которого совпадало бы с исходным изменением; возрастающее изменение потока привело бы к еще большему увеличению индукционного тока, что сопровождалось бы еще большим изменением потока. В результате ток продолжал бы нарастать до бесконечности, выделяя мощность (Р= I2 R) даже после прекращения первоначального изменения. Это означало бы нарушение закона сохранения энергии. Таким образом, правило Ленца является следствием закона сохранения энергии.
 Поскольку ЭДС определяется как циркуляция напряженности электрического поля сторонних сил (см. раздел 2.1), возникновение ЭДС индукции можно трактовать как появление вихревого электрического поля, способного перемещать заряды в замкнутой цепи.
Поскольку ЭДС определяется как циркуляция напряженности электрического поля сторонних сил (см. раздел 2.1), возникновение ЭДС индукции можно трактовать как появление вихревого электрического поля, способного перемещать заряды в замкнутой цепи.
Взаимная индукция
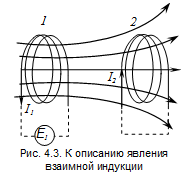
Рассмотрим опыты Фарадея более подробно. Если две катушки расположены поблизости друг от друга (рис. 4.3.), то изменение тока под действием источника переменной ЭДС E1 в одной из них приведет к появлению ЭДС индукции в другой. Это явление называют взаимной индукцией. Согласно закону Фарадея, ЭДС индукции E2 в катушке 2 пропорциональна скорости изменения пронизывающего магнитного потока. Магнитное поле, линии которого пронизывают катушку 2, создается током I1. При этом каждый виток катушки 2 пронизывает магнитный поток Ф21. Величина N2Ф21 называется потокосцеплением катушки 2, содержащей N2 витков плотной намотки.
Поскольку магнитная индукция поля, создаваемого током, всегда пропорциональна силе тока, потокосцепление катушки 2 также будет пропорционально силе тока I1 в катушке 1: N2Ф21 ~ I1.
Коэффициент пропорциональности называется взаимной индуктивностью М21 (коэффициентом взаимной индукции) катушек 1 и 2:
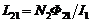 . (4.3)
. (4.3)
Единица измерения взаимной индуктивности в СИ – генри: 1Г=1Вб/А или с учетом формулы (4.1) связи потока с ЭДС: 1 Г=1 В×с/А= 1 Ом×с.
В соответствии с (4.2) и с учетом (4.3) ЭДС E2, возбуждаемая в катушке 2 изменяющимся током в катушке 1, равна
![]() .
.
Мы получили выражение, связывающее ЭДС индукции в катушке 2 с током в катушке 1. Взаимная индуктивность L21 катушки 2 по отношению к катушке 1 зависит от размеров, формы, числа витков и взаимного расположения двух катушек, Например, чем ближе катушки на рис. 4.3 друг к другу, тем больше силовых линий пройдет через катушку 2 и тем больше будет коэффициент взаимной индукции L21.
Взаимная индуктивность зависит также от материала сердечника — железа или другого ферромагнетика. При заполнении поля такой средой взаимная индуктивность увеличивается в m раз, где m — относительная магнитная проницаемость вещества. Физический смысл этой величины будет рассмотрен в разделе 5.2.
Рассмотрим теперь обратный случай, когда изменяющийся под действием внешней переменной ЭДС ток в катушке 2 возбуждает ЭДС в катушке 1. В этом случае: 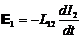 , где L12 — коэффициент взаимной индукции катушки 1 по отношению к катушке 2. Можно показать, что L12 = L21.
, где L12 — коэффициент взаимной индукции катушки 1 по отношению к катушке 2. Можно показать, что L12 = L21.
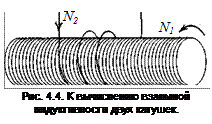 Найдем взаимную индуктивность длинного тонкого соленоида длиной l с площадью поперечного сечения S, содержащего N1 витков плотной намотки и намотанной поверх него изолированным проводом катушки с числом витков N2 (рис. 4.4), считая, что весь магнитный поток соленоида (катушки 1) проходит через катушку 2.
Найдем взаимную индуктивность длинного тонкого соленоида длиной l с площадью поперечного сечения S, содержащего N1 витков плотной намотки и намотанной поверх него изолированным проводом катушки с числом витков N2 (рис. 4.4), считая, что весь магнитный поток соленоида (катушки 1) проходит через катушку 2.
Как следует из (4.3), для этого необходимо найти поток Ф21, пронизывающий плоскость каждого витка катушки 2. По определению поток равен Ф21=B1S,
где 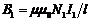 — индукция магнитного поля, созданного соленоидом (см. формулу (3.15)), имеющим сердечник, выполненный из материала с относительной магнитной проницаемостью m. Подставив выражение для потока в (4.3), получим:
— индукция магнитного поля, созданного соленоидом (см. формулу (3.15)), имеющим сердечник, выполненный из материала с относительной магнитной проницаемостью m. Подставив выражение для потока в (4.3), получим:
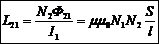 (4.4)
(4.4)
Взаимная индукция используется в трансформаторах, а также во всех случаях, когда необходимо передать электрический сигнал на малое расстояние без использования гальванической (проводной) связи между цепями.
Иногда, однако, из-за индуктивной связи возникают проблемы. Цепи переменного тока (линии передачи электроэнергии, трансформаторы) способны возбуждать ЭДС в других цепях. Даже если взаимная индуктивность невелика, слабый сигнал частоты переменного тока 50 Гц (фон), наведенный на вход усилителя музыкального комплекса, может испортить впечатление от прослушивания музыкального произведения. Для ослабления наводок обычно применяют экранированные кабели, внутренний проводник в которых окружен заземленным цилиндрическим металлическим экраном, а также стремятся уменьшать длину защищаемой от наводок цепи с целью уменьшения взаимной индуктивности. Явление самоиндукции. Ток при замыкании и размыкании цепи
Магнитный поток, создаваемый магнитным полем любого проводника, пропорционален силе тока в этом проводнике (как и магнитная индукция — см., например, формулы (3.9) и (3.12), (3.15)): Фм ~ I.
Коэффициент пропорциональности ![]() называется индуктивностью проводника. Как и взаимная индуктивность, индуктивность измеряется в генри. Значение индуктивности зависит от геометрии проводников и наличия ферромагнитного материала. Для увеличения индуктивности проводник наматывают в виде катушки, индуктивность которой зависит от числа витков и магнитной проницаемости сердечника (если он помещен в катушку). В принципе, индуктивность можно определить для любой цепи или ее части.
называется индуктивностью проводника. Как и взаимная индуктивность, индуктивность измеряется в генри. Значение индуктивности зависит от геометрии проводников и наличия ферромагнитного материала. Для увеличения индуктивности проводник наматывают в виде катушки, индуктивность которой зависит от числа витков и магнитной проницаемости сердечника (если он помещен в катушку). В принципе, индуктивность можно определить для любой цепи или ее части.
Найдем индуктивность длинного соленоида. Поток через один виток равен Фi=BS, где ![]() — индукция магнитного поля, созданного соленоидом (см. формулу (3.15)). Поток, пронизывающий все витки соленоида, равен Фм =NФi, тогда
— индукция магнитного поля, созданного соленоидом (см. формулу (3.15)). Поток, пронизывающий все витки соленоида, равен Фм =NФi, тогда
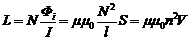 , (4.5)
, (4.5)
где n=N/l – число витков на единицу длины соленоида, V=Sl – объем соленоида.
Явление возникновения ЭДС в проводнике с током при изменении собственного магнитного потока, создаваемого этим током, называется самоиндукцией. Возникающую при этом ЭДС называют ЭДС самоиндукции:
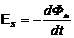 . (4.6)
. (4.6)
ЭДС самоиндукции возникает как при изменении тока, так и при изменении индуктивности. Действительно, если подставить в (4.6) выражение для магнитного потока в виде 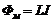 , то получим:
, то получим:
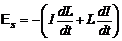
Если индуктивность не зависит от тока и является постоянной величиной, ЭДС самоиндукции определится как[2]:
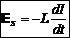 . (4.7)
. (4.7)
|
|
Явление самоиндукции можно наблюдать на опыте (рис. 4.5). При замыкании цепи лампа Л2, включенная в цепь с катушкой индуктивности (индуктивность изображается символом ![]() ), загорается позже, чем лампа Л1, включенная последовательно с резистором.
), загорается позже, чем лампа Л1, включенная последовательно с резистором.
В момент замыкания ключа, соединяющего цепь с источником тока, в цепи возникает нарастающий ток, вызывающий появление в катушке ЭДС самоиндукции, препятствующей увеличению тока. Однако по мере возрастания силы тока напряжение на лампе Л2 увеличивается, а на индуктивности — уменьшается. Таким образом, ток в цепи постепенно нарастает и приближается к максимальному значению, примерно такому же, как в лампе Л1. Резистор R, включенный последовательно этой лампе, как раз и служит для подбора одинакового тока в двух лампах.
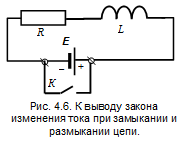 Процесс нарастания тока в цепи можно описать математически, применив к цепи[3], изображенной на рис. 4.6, правило Кирхгофа. Поскольку любая катушка индуктивности обладает электрическим сопротивлением, реальную катушку мы представили в виде последовательно соединенных индуктивности L и резистора R. Сопротивление источника тока не учитываем.
Процесс нарастания тока в цепи можно описать математически, применив к цепи[3], изображенной на рис. 4.6, правило Кирхгофа. Поскольку любая катушка индуктивности обладает электрическим сопротивлением, реальную катушку мы представили в виде последовательно соединенных индуктивности L и резистора R. Сопротивление источника тока не учитываем.
В момент размыкания ключа К в замкнутой цепи появляется ЭДС источника E и при нарастании тока I в цепи возникает ЭДС самоиндукции катушки
ES = —L(dI/dt). На основании второго правила Кирхгофа (см. раздел 2.4) составляем уравнение:
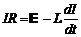 .
.
Мы получили линейное дифференциальное уравнение, которое можно решить методом разделения переменных. Приведем его к виду: 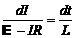 и проинтегрируем левую и правую части:
и проинтегрируем левую и правую части:
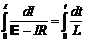 , откуда
, откуда ![]() .
.
Потенцируя данное выражение, получаем: ![]() . Приведем последнее к виду:
. Приведем последнее к виду: 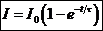 , (4.8)
, (4.8)
где I0 =E /R – установившееся значение тока, t = L/R – постоянная времени цепи. Значение t = t есть время, за которое сила тока достигает величины I0(1 — 1/е)= 0,63 I0, или 63% от своего установившегося значения.
Если перебросить переключатель K (рис. 4.6) в положение, при котором источник тока замыкается (выключается из цепи) в тот момент, когда сила тока в цепи была равной I0, то ток в цепи начинает уменьшаться и возникающая ЭДС индукции будет направлена так, чтобы замедлять его уменьшение.
На основании второго правила Кирхгофа составим уравнение для этого случая: 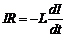 . Разделим переменные и проинтегрируем левую и правую части:
. Разделим переменные и проинтегрируем левую и правую части: 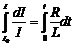 , откуда
, откуда ![]() или
или
![]() . (4.9)
. (4.9)
Таким образом, ток экспоненциально убывает до нуля. При t = t ток составляет I0/е = I0/2,71.
Поскольку реальные цепи всегда обладают индуктивностью, пусть даже малой индуктивностью соединительных проводов, ток при включении цепи достигает максимального значения с некоторой задержкой.
[1] Имеются сведения, что Джозеф Генри (1797-1878) сделал открытие раньше Фарадея, но Фарадей первым опубликовал свои результаты и провел более детальные исследования.
[2] Индуктивность катушки может зависеть от силы тока в ней, если имеется ферромагнитный сердечник.
[3] Использовать в практических целях данную схему не рекомендуется, так как замыкание ключом К источника тока приводит к выводу его из строя.
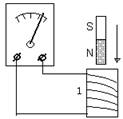
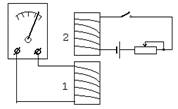
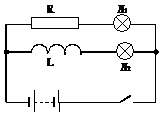 Рис. 4.5. Схема для демонстрации явления самоиндукции.
Рис. 4.5. Схема для демонстрации явления самоиндукции.

