Частные случаи приведения произвольной системы сил

Если (=0 и =0) главный вектор и главный момент относительно любого центра равен нулю, то имеем условие равновесия произвольной системы сил.

Эти уравнения представляют уравнения равновесия системы сил в пространстве в аналитической форме.

Таким образом для равновесия любой произвольной системы сил в пространстве необходимо и достаточно, чтобы сумма проекций на каждую координатную ось и сумма их моментов относительно каждой оси равнялись нулю.

·  Главный вектор не зависит от центра приведения.

·  Скалярное произведение главного вектора и главного момента для любого центра приведения есть константа.

Частные случаи приведения произвольной системы сил:

1) 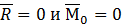, т. е. условие равновесия системы сил.

2)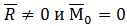 т. е. система приводится к силе, равной главному вектору, приложенному к центру приведения. Тело может совершать поступательное движение.

3) 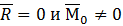, т. е. система приводится к паре сил с моментом M. Тело совершает вращательное движение.

4) 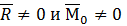и параллельны.

Так как M свободный вектор его можно переместить, тогда будет осуществляться поворот и перемещение. Тело может двигаться поступательно и вращаться, точки будут описывать винтовые линии.

5) 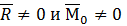и перпендикулярны. Тело может находиться в поступательном движении.

Вычислим :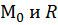

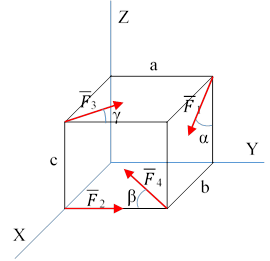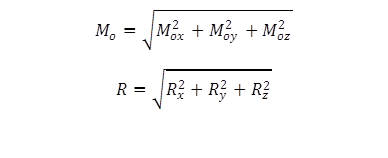Определение реакций связи в пространственной конструкции

Указать реакции или составляющие шарниров, составить уравнения равновесия.

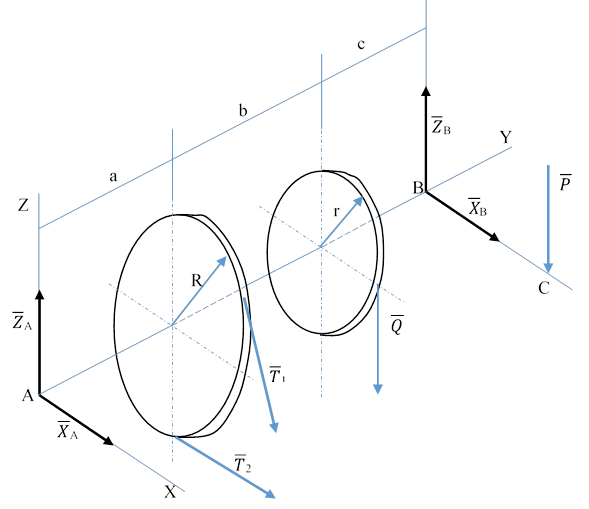
Сумма проекций на координатные оси:

Сумма моментов относительно координатных осей:

Решив эти уравнения, можно найти все неизвестные силы. В конце решения необходимо сделать проверку.

Плоская система тел. Расчет плоской фермы

Плоская система тел –составная конструкция, которая может состоять из двух или более компонентов.

Алгоритм решения:

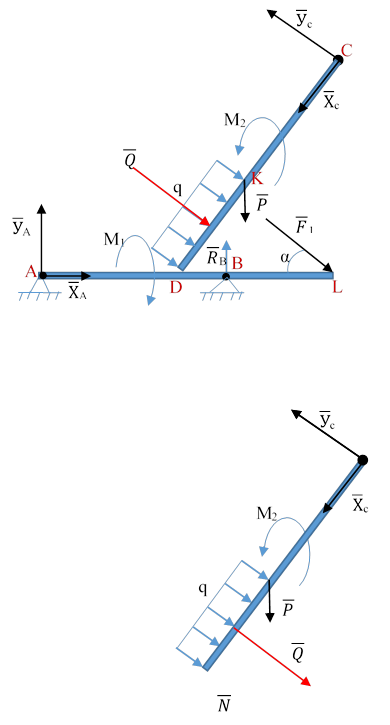
Составная конструкция расчленяется на самостоятельные объекты, определяются реакции связи и силы взаимодействия между частями, применяя принцип освобождаемости от связи.

Применяем принцип освобождаемости от связи, расчленяем конструкцию.

Сумма проекций сил на оси Х и У:

Сумма моментов относительно точки С:

Составим уравнения для второй балки.

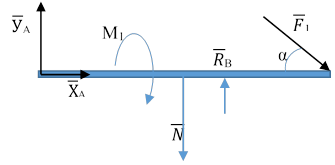Сумма проекций сил на оси Х и У:

Сумма моментов относительно точки А:

Расчет плоской фермы

Ферма-жесткая конструкция, состоящая из прямолинейных стержней и соединенных шарнирами – узлами.

n – количество узлов, k – количество стержней

Усилие прикладывается только к узлам.

Расчет фермы сводится к:

1)  определению реакций внешних связей;

2)  определению усилий в стержнях ферм:

1.  графическое построение диаграммы;

2.  вырезание узлов.

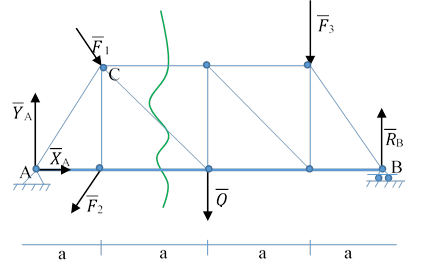Вырезание узлов. Разрежем конструкцию на две части (зеленая линия).

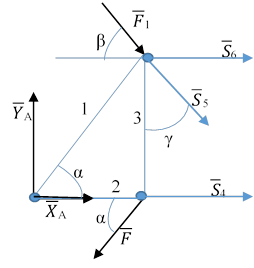Сумма проекций сил на оси Х и У:

Сумма моментов относительно точки А:

Решив эти уравнения, мы сможем найти силы сжимающие или растягивающие стержни.

Силы трения и сцепления

Трение — процесс взаимодействия тел при их относительном движении (смещении) либо при движении тела в газообразной или жидкой среде. Трение образуется при движении тел и практически не зависит от скорости.

Термин «сцепление» используется тогда, когда тело находится в покое.