Четырехмерный вектор скорости частиц
Здесь мы приняли ![]() , т. к. точку можно поместить в начало координат.
, т. к. точку можно поместить в начало координат.
2. Четырехмерный вектор скорости частиц. Определяется как
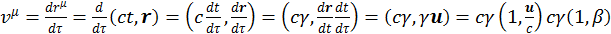
Откуда следует, что скалярное произведение
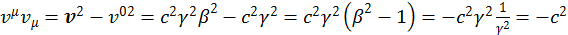 (1.7.8)
(1.7.8)
Окончательно получаем, что 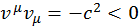 — временеподобный вектор.
— временеподобный вектор.
3. Четырехмерный вектор ускорения. Определяется как
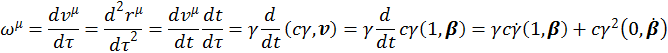
Вычислим ![]() :
:
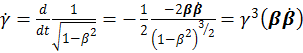 (1.7.9)
(1.7.9)
Подставим это значение ![]() в выражение для ωμ:
в выражение для ωμ:
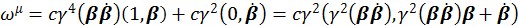 (1.7.10)
(1.7.10)
![]()
Убедиться в пространственноподобности можно, если рассмотреть ωμ в состоянии покоя ![]() :
:
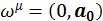 (1.7.11)
(1.7.11)
Можно показать, что четырехмерные вектора скорости vμ и ускорения ωμ взаимно ортогональны в четырехмерном пространстве: ![]()
![]() . Покажем это. Продифференцируем скалярное произведение:
. Покажем это. Продифференцируем скалярное произведение:
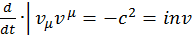 (1.7.12)
(1.7.12)
Откуда получаем, что 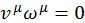 .
.
§ 1.8. Четырехмерные тензоры
Все физические величины в специальной теории относительности по характеру преобразований при переходе из одной инерциальной системе отсчета к другой являются тензорами определенного ранга (нулевого, первого, второго,…).
Тензоры нулевого ранга – скалярные величины, которые при переходе от одной инерциальной системы отсчета к другой вообще не преобразуются. Иначе говоря, они являются инвариантами. К таким тензорам нулевого ранга относятся электрический заряд частицы, скорость света, собственное время, все скалярные величины четырехмерных векторов.
Тензоры первого ранга – все четырехмерные векторы.
Тензоры второго ранга определяется аналогично четырехмерным векторам:
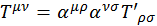 (1.8.1)
(1.8.1)
Запишем тензор Tμν в общем виде:
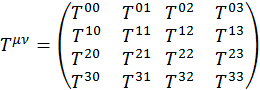
Тензором ранга назовем совокупность ![]() чисел, преобразующихся по закону:
чисел, преобразующихся по закону:
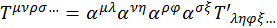 (1.8.2)
(1.8.2)
Дальше наибольшее применение получат тензоры второго ранга. Оказывается, что тензоры второго ранга могут быть симметричными и антисимметричными.
![]()
![]()
Оказывается, что любой тензор второго ранга можно представить в виде суммы симметричного и антисимметричного тензоров. Запишем произвольный тензор Тμν в виде:
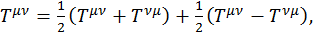 (1.8.3)
(1.8.3)
где 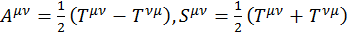 .
.
Особый интерес представляют антисимметричные тензоры. Они обладают свойством, что у них все диагональные элементы равны 0, т. е. 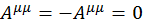 .
.
Таким образом, произвольный антисимметричный тензор имеет вид:
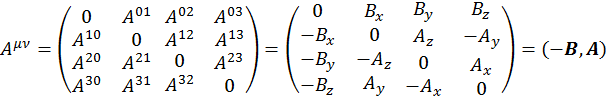 (1.8.4)
(1.8.4)
Одним замечательным свойством тензоров такого рода является то, что если взять скалярное произведение антисимметричного тензора с двумя одинаковыми векторами, то оно будет равно нулю: 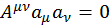 . Докажем это:
. Докажем это:
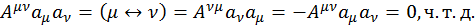 (1.8.5)
(1.8.5)
Антисимметричные тензоры, как и все четырехмерные векторы могут быть пространственноподобными:
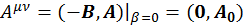 (1.8.6)
(1.8.6)
У всех антисимметричных тензоров между пространственноподобными компонентами существует связь: 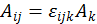 , где
, где ![]() — символ Леви-Чевита.
— символ Леви-Чевита.
Обратное соотношение имеет вид: 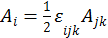 .
.
§ 1.9. Преобразование Лоренца для антисимметричного тензора
Как мы уже выяснили, любой антисимметричный тензор преобразуется по закону:
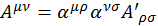 (1.9.1)
(1.9.1)
Вспомним, что
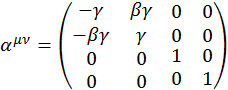 (1.9.2)
(1.9.2)
Распишем одну из компоненту антисимметричного тензора по правилу. Получим
![]()
Следовательно, 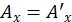 , т. е. продольная компонента не преобразуется.
, т. е. продольная компонента не преобразуется.
Проведя такие же вычисления для остальных компонент антисимметричного тензора, получим
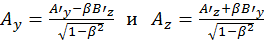 (1.9.3)
(1.9.3)
Таким же образом получены
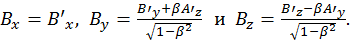 (1.9.4)
(1.9.4)
§ 1.10. Электромагнитные потенциалы и поля
Если в определении произвольного четырехмерного 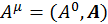 вектора за нулевую компоненту принять скалярный потенциал φ, а за векторную компоненту — трехмерный вектор-потенциал, то мы получим определение четырехмерного вектора-потенциала
вектора за нулевую компоненту принять скалярный потенциал φ, а за векторную компоненту — трехмерный вектор-потенциал, то мы получим определение четырехмерного вектора-потенциала 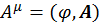 . С помощью этого вектора можно определить тензор напряженностей электромагнитного поля:
. С помощью этого вектора можно определить тензор напряженностей электромагнитного поля:
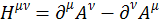 . (1.10.1)
. (1.10.1)


