Четырехвектор энергии-импульса

При малых скоростях, когда справедлив второй закон Ньютона. Процедура суммирования приводит к известному уравнению, выражающему теорему об изменении кинетической энергии, и в левой части оказывается выражение кинетической энергии. Так что уравнение (4) следует рассматривать как обобщение теоремы об изменении кинетической энергии. Левая часть уравнения (4) имеет размерность энергии, причем для покоящейся частицы она равна нулю. По аналогии с соответствующим описанием данной ситуации в ньютоновской механике, величину W следует называть кинетической энергией.

Задача 1. Рассмотрите случай малых импульсов, когда p<<m0c, и получите выражение кинетической энергии частицы.

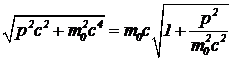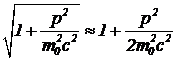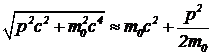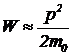Решение. Представим радикал в выражении кинетической энергии в виде . По условию, под радикалом величина, мало отличающаяся от единицы. Приближенно, , поэтому , и , что совпадает с классическим выражением кинетической энергии. Здесь надо обратить внимание на то, что классическое выражение является приближением, справедливым только в предельном случае малых скоростей.

Задача 2. Покажите, что кинетическая энергия частицы может быть представлена в виде .

Решение. В формулу 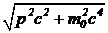подставим импульс, выраженный через скорость 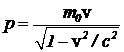. Тогда получим = =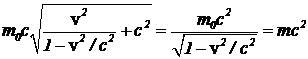, где m — релятивистская масса. Подстановка в выражение кинетической энергии дает искомый результат.

Полученное выражение дает еще один смысл кинетической энергии частицы — она показывает, на сколько релятивистская масса превышает массу покоя частицы.

2.2 Полная энергия

Слагаемое
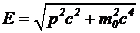(5)
называется полной энергией частицы. Полная энергия покоящейся частицы равна . Ее называют энергией покоя. Эту энергию можно выделить. Как это сделать? Физики установили, что у каждой частицы есть пара — античастица. Например, у электрона античастицей является позитрон. Он во всех отношениях, кроме заряда, похож на электрон. Античастицы имеют заряд противоположный заряду своего двойника. При соединении частицы с античастицей происходит аннигиляция, одним из результатов которой может быть рождение электромагнитной волны. Энергия возникшей волны равна полной релятивистской энергии взаимодействующих частиц, включающей и энергию покоя.

Задача 3. Если бы удавалось сохранять и затем управляемо расходовать энергию, выделяющуюся при аннигиляции, то на сколько времени эксплуатации в квартире хватило бы одного миллиграмма антиматерии? (Считайте, что месячный расход электроэнергии равен 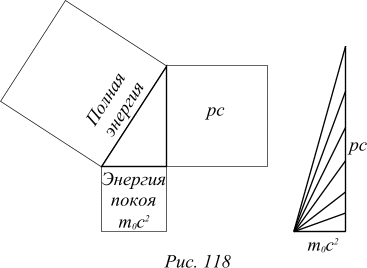500 кВт×час.)

Выражение (5) напоминает теорему Пифагора. При ускорении частицы ее импульс растет, как катет прямоугольного треугольника, а полная энергия растет, как гипотенуза. Энергия покоя — не зависящий от разгона катет. При небольших скоростях прирост импульса приводит к малым изменениям энергии, потому что у очень низких треугольников гипотенуза почти равна горизонтальному катету. Это случай медленных движений (обычная механика Ньютона). Потом энергия начинает расти быстрее и быстрее. При скоростях, близких к скорости света, треугольник сильно вытянут вверх: в таком треугольнике гипотенуза почти равна вертикальному катету. То есть при быстром движении стирается разница между энергией и импульсом (умноженным на скорость света): E»pc. До такой степени разогнанные частицы называют ультрарелятивистскими.

Полная энергия частицы наиболее компактно записывается через релятивистскую массу m в виде
E=mc2. (6)
Это знаменитая формула Эйнштейна. Она устанавливает факт тож­дественности энергии и массы частиц.

В левую часть уравнения (5) входят все виды энергии – не только кинетическая, но и потенциальная энергия взаимодействия. Так, известно, что для разрушения атомных ядер, состоящих из протонов и нейтронов, нужно совершить определенную работу. Это означает, что энергия разобранного ядра больше целого ядра. По этой причине масса ядра всегда меньше суммарной массы составляющих частиц. Разница между суммарной массой составляющих частиц и массой ядра называется дефектом массы.

Задача 4. Какой процент составляет дефект массы ядра кислорода от полной массы, если его масса равна 16 а. е.м. Масса протона, 1.00759 а. е.м, масса нейтрона, 1.00898 а. е.м. Какую работу (в электронвольтах) надо совершить, чтобы разобрать ядро на составные части?
1 а. е.м=1,66×10-27кг.

3. Четырехвектор энергии-импульса

3.1 Четырехвекторы

Пространство и время образуют единый объект — четырехмерное пространство-время. Любая точка в четырехмерном пространстве — это событие. Точка указывает — где и когда произошло событие. Векторные величины в этом пространстве имеют четыре проекции: проекцию на временную ось (временную компоненту) и три проекции на пространственные оси (пространственные компоненты). Вектор, проведенный из начала координат в точку четырехмерного пространства-времени (до события), будем называть четырехмерным радиус-вектором. Четырехмерный радиус-вектор события имеет проекции {ct, x, y, z}. Четырехмерное пространство-время отличается от трехмерного не только числом компонент, но и правилом вычисления модуля вектора, который в любой системе отсчета остается одним и тем же (он инвариантен относительно преобразований Лоренца). Модулем четырехмерного радиус-вектора является интервал между событием в начале координат и в заданной точке пространства-времени:
. (6)
Как было ранее показано, интервал между двумя событиями во всех системах отсчета один и тот же.

3.2 Четырехвектор энергии-импульса

Если выражение полной энергии (5) переписать в виде
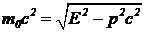, (7)
то в глаза бросается сходство с выражением (6). Сходство усиливается тем, что величина во всех системах отсчета одна и та же. Детальные (но кропотливые) расчеты показывают, что при переходе из одной инерциальной системы отсчета в другую проекции импульса px, py, pz преобразуются точно так же, как проекции радиус-вектора x, y, z. Из этого можно заключить, что энергия и импульс являются временной и пространственной компонентами единого четырехмерного вектора. Модуль этого четырехвектора энергии-импульса равен . Понятно, почему величину m0 назвали инвариантной массой.

Энергия и импульс имеют разные размерности. Чтобы уравнять в правах компоненты четырехвектора энергии-импульса, используют величины: либо временную компоненту в форме E/c (тогда она имеет размерность импульса), либо пространственную в форме pc (тогда она имеет размерность энергии) — {E, pxc, pyc, pzc}, или {E/c, px, py, pz}.

При переходе в новую инерциальную систему отсчета компоненты четырехвектора энергии-импульса преобразуются точно так же, как компоненты четырехмерного радиуса-вектора события: импульсы — как пространственные координаты события, а энергия — как момент времени. При переходе из одной инерциальной системы отсчета в другую для энергии и импульса частицы справедливы преобразования Лоренца.

Задача 5. Выпишите преобразования Лоренца для импульса и энергии частицы. Используя полученные преобразования, проверьте, что во всех системах отсчета величина E2-p2c2 принимает одно и то же значение.

Пусть штрихованная и лабораторная системы отсчета имеют взаимно параллельные оси координат и относительную скорость, направленную вдоль оси OX. Каждое из уравнений следует получать, сопоставляя требуемое преобразование с преобразованием соответствующей компоненты четырехмерного радиус-вектора, с учетом размерностей. Тогда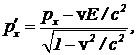
(8)
p`y=py; (9)
p`z=pz; (10)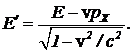
(11)