Полярные диэлектрики
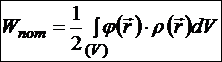
потенциал — это потенциал, созданный всем зарядом системы, распределённым по объёму V, в точке ![]() , принадлежащей этому объёму.
, принадлежащей этому объёму.
При распределении заряда по поверхности интегрирование, очевидно, нужно проводить по поверхности, поскольку элементарным зарядом будет заряд ![]() .
.
Контрольные вопросы к главе 14
 1. Можно ли придумать систему источников, электростатическое поле которых имело бы одноосную неоднородность? Например:
1. Можно ли придумать систему источников, электростатическое поле которых имело бы одноосную неоднородность? Например: 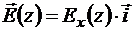 . Силовые линии такого поля могут выглядеть так, как показано на рисунке. (Ответ: нет) (§14.1)
. Силовые линии такого поля могут выглядеть так, как показано на рисунке. (Ответ: нет) (§14.1)
2. При разряде молнии переносится заряд Q= 40 Кл, причем разность потенциалов между концами молнии достигает значения U= 35 МВ. Какая энергия при этом выделяется? (Ответ: »1,4×109Дж) (§14.2)
3. Поле потенциала в декартовых осях описывается соотношением: 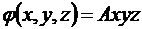 , где А=8×10-3 В/м3. Чему равен модуль напряжённости электростатического поля в точке с координатами х=5 см, y=1 см, z=0? Чему равен угол между вектором напряжённости и осью z в этой точке? (Ответ: 4×10-6В/м; 180°) (§14.3)
, где А=8×10-3 В/м3. Чему равен модуль напряжённости электростатического поля в точке с координатами х=5 см, y=1 см, z=0? Чему равен угол между вектором напряжённости и осью z в этой точке? (Ответ: 4×10-6В/м; 180°) (§14.3)
4. В электронной лампе электроны вылетают из катода, представляющего собой раскалённую металлическую пластину, и собираются на аноде, представляющую собой точно такую же металлическую пластину (холодную), расположенную параллельно катоду напротив него на расстоянии 8 мм, значительно меньшем размеров пластин. Потенциал электрического поля между пластинами меняется по закону 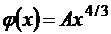 (А=15 В/м4/3), где х — расстояние до катода. Чему равны плотности поверхностных зарядов на катоде и аноде? (Ответ: 0; 35,4×10-12Кл/м2) (§14.3)
(А=15 В/м4/3), где х — расстояние до катода. Чему равны плотности поверхностных зарядов на катоде и аноде? (Ответ: 0; 35,4×10-12Кл/м2) (§14.3)
5. Определите линейную плотность заряда τ бесконечно длинной заряженной нити, если работа сил поля по перемещению положительного заряда Q= 10-9 Кл с расстояния r1=0,4 м до расстояния r2=0,1 м в направлении, перпендикулярном нити, равна A=10-3 Дж. (Ответ: »-4×10-5Кл/м) (§14.5)
 6. Какую работу нужно совершить, чтобы шесть одинаковых зарядов, равных 2 нКл и бесконечно удалённых друг от друга, перенести в вершины равностороннего шестиугольника со стороной 4 см? (Ответ: »10 мкДж) (§14.6)
6. Какую работу нужно совершить, чтобы шесть одинаковых зарядов, равных 2 нКл и бесконечно удалённых друг от друга, перенести в вершины равностороннего шестиугольника со стороной 4 см? (Ответ: »10 мкДж) (§14.6)
 7. Металлический шар радиусом R1=1 м заряжен зарядом -1 мКл и окружён заземлённой сферической оболочкой радиусом R2=9 м. Чему равна энергия такой системы? (Ответ: 4 кДж) (§14.6)
7. Металлический шар радиусом R1=1 м заряжен зарядом -1 мКл и окружён заземлённой сферической оболочкой радиусом R2=9 м. Чему равна энергия такой системы? (Ответ: 4 кДж) (§14.6)
8. Заземлённый металлический шар радиусом R1=1 м окружён сферической оболочкой радиусом R2=3 м, заряженной зарядом 1 мКл. Чему равна энергия такой системы? (Ответ: 3 кДж) (§14.6)
Глава 15. ЭЛЕКТРОСТАТИКА.
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИЧЕСКОЙ СРЕДЕ
§15.1. Диэлектрическая среда
С понятием среды вы впервые могли столкнуться при изучении механики жидкости. Повторим ещё раз. Среда − это материя, обладающая массой покоя, которая непрерывно заполняет пространство. Ключевым в определении среды является слово «непрерывно». Это значит, что среда представляется чем-то однородным, тем, что можно дробить бесконечно, не боясь, что свойства бесконечно малой части будут отличаться от свойств конечного целого. Такое представление о материи является идеализацией, поскольку исключает из рассмотрения ее микроскопическое строение, то есть молекулярно-атомное строение «массовой» материи. Бесконечно малое с точки зрения понятия среды количество вещества включает в себя макроскопическое (порядка числа Авогадро) количество молекул. Все характеристики среды в данной точке пространства являются результатом усреднения микроскопических характеристик по этой огромной совокупности микрочастиц. Таким образом, все точечные характеристики среды являются макроскопическими характеристиками. Но объяснить, почему свойства одной среды отличаются от свойств другой, невозможно без обращения к микроскопическим моделям строения материи.
Мы будем придерживаться следующей терминологии. Заряд, который не относится к рассматриваемой среде (внешний по отношению к ней) будет называться свободным. При этом термин «несвободный» использоваться не будет. Заряды, принадлежащие среде, в электростатике будут разделяться на два вида. Если заряды среды способны передвигаться на макроскопическое расстояние, то они называются несвязанными. Если заряды среды могут смещаться из положения равновесия только на микроскопическое расстояние, то они называются связанными. Диэлектрики − это среды, в которых отсутствует макроскопическое количество несвязанного заряда. Микроскопические количества при рассмотрении среды в расчёт не принимаются, следовательно, все заряды диэлектрической среды − связанные.
В зависимости от строения молекул диэлектрические среды делятся на два класса: неполярные и полярные диэлектрики.
§15.2. Неполярные диэлектрики
В отсутствие электрического поля молекулы неполярных диэлектриков не имеют дипольного момента. Это означает, что «центр тяжести» электронного облака совпадает с центром положительного заряда молекулы. При наложении электрического поля электронное облако смещается в направлении, противоположном полю.
 Рис.15.1
Рис.15.1
В результате, на молекуле возникает индуцированный дипольный момент ![]() , направленный по полю.
, направленный по полю.
Неполярная молекула подобна упругой пружине, которая растягивается пропорционально растягивающей силе, то есть пропорционально прилагаемому электрическому полю. Значит, плечо диполя пропрционально Е. Коэффициент пропорциональности запишем в виде ae0. Следовательно,
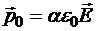 .
.
Величина a называется поляризуемостью молекулы (имеет физическую размерность).
Тепловое движение неполярных молекул никак не влияет на возникновение у них индуцированных дипольных моментов из-за очень малой инерционности электронного облака. Молекула, практически, мгновенно «подстраивается» под прилагаемое поле подобно лёгкому флагу, все время развивающемуся по сильному ветру. Итак, поляризуемость молекулы неполярного диэлектрика является только характеристикой молекулы и не зависит от температуры.
§15.3. Полярные диэлектрики
В противовес неполярным, молекулы полярных диэлектриков обладают дипольным моментом в отсутствие приложенного электрического поля и могут рассматриваться как жёсткие структуры, чья деформация под действием внешних факторов пренебрежимо мала по сравнению с исходными размерами. Подстройка таких диполей под прилагаемое поле происходит ориентационным способом.
 Рис.15.2
Рис.15.2
Из рисунка видно 15.2, что если молекулярный дипольный момент ![]() ориентирован по отношению к прилагаемому полю под углом a (
ориентирован по отношению к прилагаемому полю под углом a (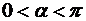 ), то на него действует вращающий момент сил, направленный на уменьшение угла. Суммарная сила, приложенная к диполю, равна 0. Следовательно, под действием поля происходит вращение дипольного момента вокруг неподвижного центра масс молекулы.
), то на него действует вращающий момент сил, направленный на уменьшение угла. Суммарная сила, приложенная к диполю, равна 0. Следовательно, под действием поля происходит вращение дипольного момента вокруг неподвижного центра масс молекулы.
Угол a на рисунке образован вращением по часовой стрелке, следовательно, по правилу правого винта его направление положительно по оси z. Направление вращающего момента отрицательно. Проекция вращающего момента на ось z:
![]() .
.
Расстояния l+ и l— от центра масс молекулы до точек приложения сил 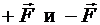 в сумме, очевидно, дадут плечо диполя l. Следовательно,
в сумме, очевидно, дадут плечо диполя l. Следовательно,
![]()


