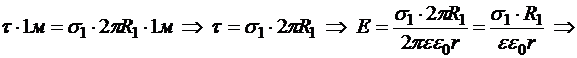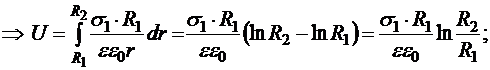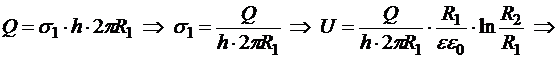Конденсаторы

Метод основан на теореме единственности, которая доказывается в теории дифференциальных уравнений. Согласно этой теореме потенциал, созданный системой зарядов на замкнутой поверхности, однозначно определяет пространственное распределение потенциала с одной стороны этой поверхности (снаружи или внутри) при условии, что источники в этой части пространства неизменны. Это значит, что конфигурация источников в противоположной части пространства (внутри или снаружи) может быть любой из тех, которые задают данное значение потенциала на данной замкнутой поверхности. Иными словами, если обеспечено значение потенциала на сферической поверхности, то для внешнего по отношению к сфере пространства не важно, что делается внутри сферы. А для внутреннего пространства сферы не важно, что делается за пределами сферы.

Рассмотрим точечный свободный заряд за пределами сферического проводника.

Рис.16.6

Линия, проходящая через свободный заряд q и центр проводника, несущего заряд Q, пересекает поверхность сферы в точках I и II, которые называются полюсами сферы по отношению к точке q (рис.16.6). Свободный заряд отстоит от полюса I на расстояние l, а от полюса II – на расстояние .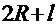

Нас будет интересовать, как наличие свободного заряда, удалённого от поверхности заряженной сферы на расстояние l, влияет на её потенциал j.

Следуя теореме единственности, мы имеем право реальное распределение заряда Q на поверхности сферы заменить удобной для расчёта конфигурацией заряда внутри сферы, так чтобы потенциал сферы оставался равным j. Эта конфигурация представлена на рисунке: заряд имеет такое значение и находится в такой точке на прямой между полюсом I и центром сферы, чтобы вместе со свободным зарядом q создать на поверхности сферы потенциал, равный 0. Заряд называется изображением источника в данной сфере. Тогда потенциал j на сфере будет создан остаточным зарядом , помещённым в центр сферы.

Определим параметры изображения q’ и l’. Для этого рассмотрим суммарный потенциал, созданный источником и изображением в полюсах сферы I и II. Как и в других точках сферы, он будет равен 0. Следовательно,

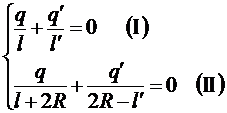
Мы имеем систему из двух уравнений с двумя неизвестными, которая легко решается. Выразим из (I) q’:

.

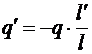Сделаем подстановку в (II):

; .

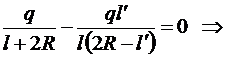
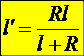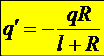Тогда потенциал сферы

где j0 – потенциал на проводнике в отсутствие свободного заряда, а 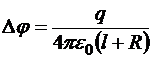– поправка, связанная с его наличием вблизи проводника.

Пусть заряд на проводнике Q=0. Будет ли нейтральная проводящая сфера взаимодействовать с зарядом q? Ответить на этот вопрос − это всё равно, что ответить на вопрос: будет ли действовать на заряд q система зарядов (рис.16.7), состоящая из изображения q’ и остаточного заряда (-q’)?

Рис.16.7

Из формул электростатического изображения точечного заряда в проводящей сфере видно, что изображение имеет знак, противоположный источнику q, а знак остаточного заряда будет совпадать со знаком источника.

Следовательно, изображение будет притягивать, а остаточный заряд отталкивать источник q. Но, поскольку изображение ближе остаточного заряда, то его влияние больше, и точечный заряд будет притягиваться нейтральной проводящей сферой.

В качестве заряда, свободного по отношению к данному проводнику может выступать не только точечный заряд, но и нескомпенсированный заряд другого проводника. Взаимное влияние двух заряженных проводников друг на друга приведёт к установлению на них потенциалов, существенно отличающихся от их потенциалов, как уединённых проводников. Если заряды на двух проводниках одинаковы по величине и противоположны по знаку, то можно ввести понятие взаимной электроёмкости двух проводников:

,

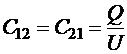где Q − модуль заряда одного из проводников, U − модуль разности потенциалов между ними (напряжение). Взаимная ёмкость будет определяться только размерами и формой проводников, а также их взаимным расположением.

§16.6. Конденсаторы

Конденсатором называется система из двух проводников, заряды которых равны по величине и противоположны по знаку, а суммарное электростатическое поле сосредоточено в ограниченной области пространства вблизи них. Емкость конденсатора — это взаимная ёмкость составляющих его проводников.

16.6.1. Плоский конденсатор.

Здесь в качестве проводников выступают две одинаковые пластины, расположенные против друг друга параллельно друг другу так, что расстояние между ними d значительно меньше их размеров. Пространство между пластинами заполнено диэлектрической средой с диэлектрической проницаемостью e (рис.16.8).

Пренебрегая краевыми эффектами можно считать распределение заряда по пластинам и электростатическое поле между ними однородным. Очевидно, что за пределами этой области поля пластин скомпенсируют друг друга. По теореме ОГ напряжённость поля в полости конденсатора

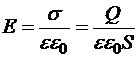
Напряжение между пластинами связано с напряжённостью по формуле однородного поля:

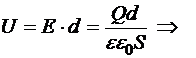
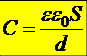
16.6.2. Сферический конденсатор

В качестве проводников выступают две концентрические сферы, сферический слой между которыми заполнен диэлектрической средой с диэлектрической проницаемостью e. Очевидно, что за пределами внешней сферы поле отсутствует, так как суммарный охваченный заряд равен 0. В полости конденсатора поле определяется только зарядом внутренней сферы. Для интервала радиусов

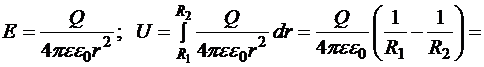
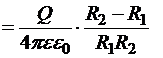Þ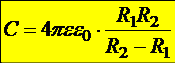

16.6.3. Цилиндрический конденсатор

В качестве проводников выступают два коаксиальных цилиндра, высота h которых значительно больше большего радиуса. Цилиндрический слой между пластинами заполнен диэлектрической средой с диэлектрической проницаемостью e (рис.16.9). Пренебрегая торцевыми эффектами можно считать, что поле в полости конденсатора создано только зарядом внутреннего цилиндра, а за пределами внешнего отсутствует. Для интервала радиусов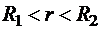

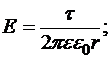
Заряд единицы высоты внутреннего цилиндра: