Батареи конденсаторов

Þ .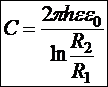

Для любого типа конденсаторов очевидно следующее утверждение: если конденсатор заряжен, то на нем есть напряжение; если на конденсаторе есть напряжение, то он заряжен.

§16.7. Батареи конденсаторов

Батареей конденсаторов называется любое соединение нескольких конденсаторов такое, что между левой и правой клеммами схемы нет короткого замыкания. Напряжение между крайними клеммами будем называть общим напряжением батареи Uобщ. Схема соединения конденсаторов рассматривается в качестве батарее только в том случае, если на крайние обкладки батареи помещается одинаковый по величине и противоположный по знаку заряд, модуль которого Qобщ называется общим зарядом батареи. По определению ёмкостью батареи называется отношение их её общего заряда к её общему напряжению. Ёмкость батареи зависит только от ёмкостей составляющих её отдельных конденсаторов и от способа их соединения. Следовательно, любую батарею можно заменить одним конденсатором, ёмкость которого равна емкости батареи.

16.7.1. Последовательное соединение

Рис.16.10

Заряд является общим для всех конденсаторов, напряжение батареи является суммой напряжений отдельных конденсаторов:

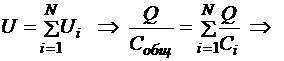
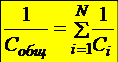
16.7.2. Параллельное соединение

Общим для всех конденсаторов является напряжение. Заряд батареи равен сумме зарядов отдельных конденсаторов.

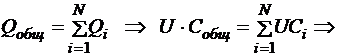
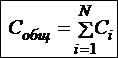
16.7.3. Мостиковое соединение

В случае произвольных ёмкостей С1, С2, С3, С4 схема, представленная на рисунке 16.12 не сводится ни к последовательной, ни к параллельной. Учебная практика такова, что, практически, любая предлагаемая для расчёта батарея представляет собой либо глобально последовательную, либо глобально параллельную схему соединений. Мостиковая схема сводится одновременно и к параллельной, и к последовательной при условии уравновешенности мостика:

Рис.16.12

.

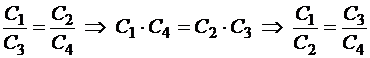В этом случае разность потенциалов на мостиковой ёмкости С0 равна 0 и её можно либо заменить коротким замыканием (получится глобально последовательная схема), либо вообще игнорировать (получится глобально параллельная схема). Если же мостик неуравновешен, то бесполезно пытаться представить батарею через последовательно-параллельную схему. Тогда нужно составлять систему линейных уравнений относительно зарядов и напряжений конденсаторов, выделяя узлы схемы (суммарный заряд обкладок, выходящих на данный узел, равен 0) и разбивая схему на смежные контуры (сумма напряжений в каждом контуре равна 0).

§16.8. Энергия электростатического поля

Вспомним формулу энергии системы распределённого заряда, полученную ранее:

,

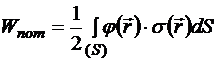где − потенциал, созданный в данной точке всем распределённым зарядом; − поверхностная плотность заряда в данной точке (мы будем иметь в виду заряд, распределённый по поверхности).

Рассмотрим уединённый проводник, несущий на себе нескомпенсированный заряд Q. Потенциал, который при этом имеет проводник, обозначим j. Интеграл потенциальной энергии такой системы примет вид:

.

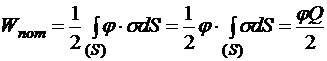Используя определение ёмкости уединённого проводника, можем выразить заряд через потенциал и ёмкость и исключить его из выражения:

.

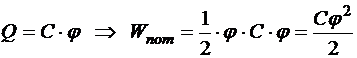Но точно также можно исключить из выражения потенциал:

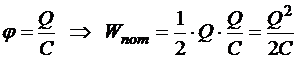
Все три полученных формулы энергии уединённого заряженного проводника являются эквивалентными и должны применяться адекватно условию задачи.

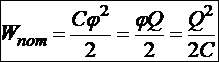
Рассмотрим заряженный плоский конденсатор. Потенциал отрицательной пластины определим равным 0. Тогда потенциал положительной пластины равен U, то есть напряжению конденсатора. При этом интегрирование сводится к положительной пластине:

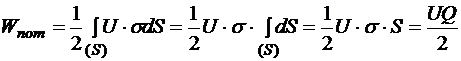
Аналогично предыдущему получаем три эквивалентные формулы энергии заряженного конденсатора:

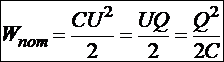
Являясь абсолютно правильными, приведённые формулы энергии наводят на мысль, что энергия системы заряженных проводников локализуется на местах расположения зарядов. Это неверно. В рамках электростатики доказать обратное невозможно, но из электродинамики, рассмотрение которой ждёт нас впереди, следует, что

энергия локализована в пространстве, окружающем заряженные тела, поскольку её материальным носителем является электростатическое поле.

Энергия заряженного плоского конденсатора сосредоточена в его полости, заполненной однородным электростатическим полем. Следовательно, и распределение энергии однородно, то есть можно найти объёмную плотность энергии электростатического поля w, поделив энергию заряженного конденсатора

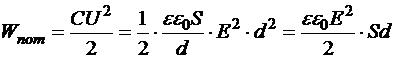
на объём его полости

.

Тогда

.

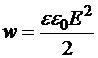Вспомним, что электростатическое поле можно характеризовать не только напряженностью, но и электрическим смещением . Тогда получим три эквивалентные формулы объёмной плотности электрического поля:

.

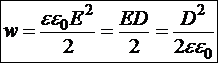§16.9. Энергия поляризованного диэлектрика

Из последней формулы следует, что объёмная плотность энергии поля в вакууме

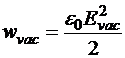
Если при неизменных источниках заполнить вакуум диэлектриком с проницаемостью e, то

,

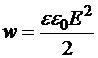где 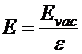− напряжённость поля в диэлектрической среде. Тогда

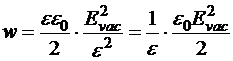
Следовательно, объёмная плотность при тех же самых источниках в вакууме в e раз больше, чем в диэлектрике. Значит, при неизменных зарядах на обкладках конденсатора электростатическое поле будет стремиться втянуть диэлектрик внутрь полости конденсатора. В результате этого, диэлектрик по сравнению с неполяризованным состоянием приобретёт приращение объёмной плотности энергии отрицательного знака:

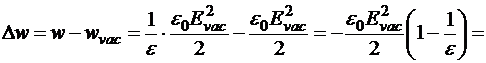
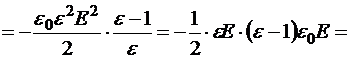
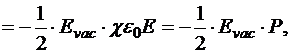
где Р − модуль вектора поляризации. В векторной форме:

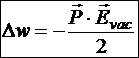
Контрольные вопросы к главе 16

1. Баскетбольный мяч лопнет, если перепад между внутренним давлением и наружным превысит 105 Па. При этом радиус мяча перед взрывом будет равен 125 мм. Какой заряд можно равномерно намазать на поверхность абсолютно пустого баскетбольного мяча, чтобы он не лопнул? (Ответ: 261093 нКл) (§16.3)