Закон Ома для однородного участка цепи
Рассмотрим произвольный источник положительной ЭДС. Являясь неоднородным участком, он обладает двумя неотъемлемыми характеристиками: сопротивлением, которое называется внутренним и обозначается буквой r, и ЭДС e. Закон Ома для неоднородного участка позволяет дать практическое определение положительной e. Сначала дадим определение: разомкнутым источником ЭДС называется источник, по которому не протекает электрический ток. Схему разомкнутого источника легко изобразить:
 Рис.17.4
Рис.17.4
Закон Ома для этого участка выглядит так:
![]() Þ
Þ 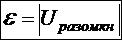
ЭДС источника равна модулю разности потенциалов на разомкнутом источнике.
§17.5. Закон Ома для однородного участка цепи (I-я форма интегрального закона Ома)
Однородным называется участок, на котором отсутствуют источники ЭДС. Электрическая схема участка выглядит так:
 Рис.17.5
Рис.17.5
На однородном участке на носитель действуют только сила сопротивления и электростатическая сила в качестве движущей. Единственной неотъемлемой характеристикой однородного участка является сопротивление R. Закон Ома для такого участка легко получается из выражения для неоднородного участка с помощью обнуления ЭДС:
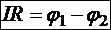 или
или 
Словесная формулировка будет звучать так:
на однородном участке цепи постоянного тока напряжение равно падению напряжения.
17.5.1. Последовательное соединение сопротивлений
 Рис.17.6
Рис.17.6
Очевидно, что через все сопротивления течёт один и тот же ток. Проинтегрируем закон Ома для элементарного участка по всему (от клеммы 1 до клеммы 2) однородному участку:
![]() .
.
Падение напряжения всего однородного участка раскладывается на сумму падений напряжения на каждом отдельном сопротивлении:
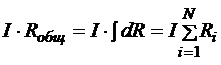 Þ
Þ 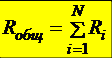 .
.
Напряжение на всем участке:
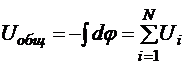
Итак, при последовательном соединении ток через все сопротивления течёт один и тот же, напряжение на всём участке равно сумме напряжений на отдельных сопротивлениях, общее сопротивление участка равно сумме отдельных сопротивлений.
17.5.2. Параллельное соединение сопротивлений
 Рис.17.7
Рис.17.7
Очевидно, что общий ток равен сумме токов через каждое сопротивление:
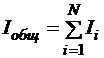 ,
,
а напряжение на всех сопротивлениях одинаковы и равны 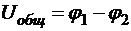 . Тогда
. Тогда
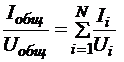 Þ
Þ 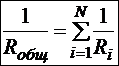
Итак, при параллельном соединении напряжение на всех сопротивлениях одно и то же, ток на всём участке равен сумме токов на отдельных сопротивлениях, общее обратное сопротивление участка равно сумме отдельных обратных сопротивлений
17.5.3. Мостиковое соединение
Аналогично соединениям (батареям) конденсаторов резисторы (сопротивления) можно соединять не только в последовательно-параллельные схемы, но и в мостиковые, которые в общем случае невозможно свести ни последовательным, ни к параллельным соединениям.
 Рис.17.8
Рис.17.8
В общем случае расчёт токов, текущих по участкам отдельных сопротивлений рассчитывается по законам Кирхгофа (далее), но при выполнении условия уравновешенности мостика
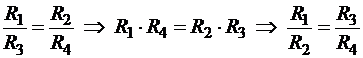
через резистор R0 ток не течёт, и его с одинаковым успехом можно заменить на короткое замыкание, сводя мостик к глобально последовательной схеме, или игнорировать, сводя схему к глобально параллельной.
§17.6. Закон Ома для простого контура (III-я форма интегрального закона Ома)
Простым контуром называется контур, состоящий из неоднородного участка (источник), замкнутого однородным участком (нагрузка):
 Рис.17.9
Рис.17.9
Проинтегрируем закон Ома для элементарного участка по всему контуру в направлении ЭДС:
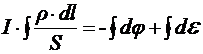
Интеграл сопротивления распадается на два интеграла: по участку источника (внутренний участок контура) и по участку нагрузки (внешний участок контура).
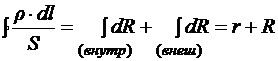 .
.
Интеграл напряжения по замкнутому контуру равен 0:
![]() .
.
Интеграл ЭДС по контуру равен ЭДС источника. В результате получаем:
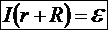 .
.
Отсюда видно, что ток в простом контуре течёт всегда по направлению ЭДС.
§17.7. Законы Кирхгофа
Законы Кирхгофа позволяют рассчитать силы токов, текущих в сложных контурах. Разветвлённым или сложным контуром называется цепь постоянного тока, состоящая из нескольких смежных простых контуров.
 Рис.17.10
Рис.17.10
На рисунке 17.10 изображён сложный контур, состоящий из двух смежных контуров. Необходимым элементом схем сложных контуров являются узлы: точки, в которые втекают и вытекают более двух токов (на рисунке отмечены кружками). Для узлов справедлив I-й закон Кирхгофа:
алгебраическая сумма токов одного узла равна 0:
.
В этой алгебраической сумме токи, втекающие в данный узел, и токи, вытекающие из данного узла, должны иметь разные знаки. Суммирование ведётся по всем токам, связанным с данным узлом. Очевидно, что I-й закон Кирхгофа является следствием уравнения неразрывности для постоянного тока.
При использовании I-го закона Кирхгофа необходимо следить за тем, чтобы обозначения токов разных узлов было единым для всей схемы, так чтобы выполнялось правило: на участке между двумя соседними узлами ток не меняет ни силы, ни направления.
Если проинтегрировать по одному простому контуру закон Ома для элементарного участка:
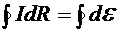 ,
,
то получим II-й закон Кирхгофа, справедливый для каждого простого контура:
алгебраическая сумма падений напряжения контура равна алгебраической сумме его ЭДС:
.
Знаки падений напряжения и ЭДС определяются по отношению к направлению обхода контура (по часовой или против часовой стрелки), которое для данного контура выбирается произвольно и независимо от выбора, сделанного для других простых контуров. Если ток течёт против направления обхода, он считается отрицательным. Если ЭДС включена против направления обхода, она считается отрицательной.
Уравнения I-го и II-го законов Кирхгофа для всего сложного контура должны составить замкнутую систему линейных уравнений, которая позволяет однозначно определить силы тока контура по ЭДС и сопротивлениям, включённым в контур. Запишем уравнения I-го и II-го законов Кирхгофа для рассматриваемого контура:
· верхний узел: ![]() (1)
(1)
· нижний узел: ![]() (1’)
(1’)
· левый простой контур: ![]() (2)
(2)
· правый простой контур: ![]() (3)
(3)


