Общий взгляд на интегральный закон Ома

Видно, что уравнения (1) и (1’) не являются линейно независимыми: (1’) получается из (1) почленным умножением на -1. Поэтому мы имеем три линейно независимых уравнения:

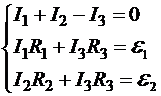
относительно трёх неизвестных:

§17.8. Общий взгляд на интегральный закон Ома.

Рис.17.11

Вы заметили, что I-я и III-я формы закона Ома получаются из II-ой обнулением соответствующих членов равенства? Точно так же и формула практического определения ЭДС. Значит, II-я форма закона Ома является центральной для теории тока. Всю теорию можно изобразить в виде «конверта» с центральной печатью и с печатями по углам (рис.17.11). На четвёртый угол «обнулений» уже не хватает. Четвёртая печать получается через почленное умножение закона Ома на силу тока. А каков физический смысл этого математического действия, Вы узнаете из следующего параграфа.

§17.9. Закон Джоуля-Ленца в интегральной форме

Этот параграф наиболее важный из всей лекции, поскольку он касается вопроса: «для чего нам нужен электрический ток?».

Умножим закон Ома для неоднородного участка цепи на силу тока на участке:

® ,

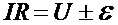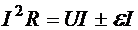и рассмотрим физический смысл каждого полученного члена.

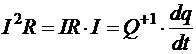. Но тепло, выделяемое при протекании единицы заряда 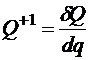, следовательно, 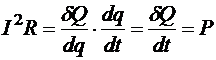— тепловая мощность участка, или количество тепла, выделяемое на участке в единицу времени, благодаря протеканию по участку электрического тока.

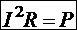
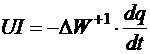. Но сброс механической энергии единицы заряда на участке 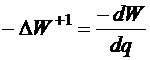, следовательно, 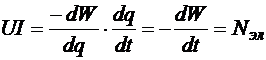— электрическая мощность участка, или количество механической энергии носителей заряда (электроэнергии), приносимой ими на данный участок и сбрасываемой на нём в единицу времени. С этим членом как раз и связан ответ на вопрос, заданный в начале параграфа. Электрический ток нам нужен для того, чтобы доставлять энергию, необходимую для работы используемых нами электроприборов.

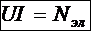
Смысл последнего слагаемого мы будем раскрывать для каждого знака по отдельности, и начнём со знака минус, то есть с участка потребителя.

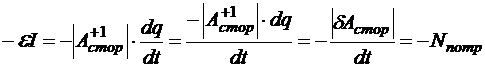, где Nпотр — мощность потребителя, то есть количество энергии, которое электроприбор выделяет в единицу времени в том виде, в каком нужно нам. Здесь становится ясен «потребительский» смысл отрицательных ЭДС. Это такое свойство различных технических устройств, благодаря которому на устройстве происходит обмен электроэнергии на другие виды энергии, нужной потребителю (кроме тепловой). Отрицательная ЭДС в электродвигателях связана с обменом электроэнергии на механическую энергию; в лампах дневного света, светодиодах — на световую; в динамиках — на акустическую; в заряжающихся аккумуляторах — на электрохимическую.

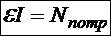
Теперь подставим выявленные физические смыслы в закон Ома для участка потребителя, почленно умноженный на силу тока:

Þ

Þ .

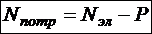Полученное соотношение означает, что количество энергии, получаемое потребителем в единицу времени, равно электроэнергии, получаемой участком потребителя, за вычетом тепла, выделяемого на участке. Как Вы понимаете, это просто закон сохранения энергии (не механической, а вообще) на участке потребителя.

Частным случаем участка потребителя является нагреватель, то есть однородный участок цепи. Поскольку на нём отсутствует ЭДС, то закон Джоуля-Ленца примет вид:

.

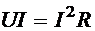Домножив и разделив правую сторону равенства на R получим: 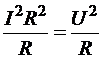с учётом закона Ома для однородного участка. Тогда получаем три эквивалентных выражения мощности участка нагревателя: электрической и двух тепловых:

.

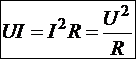При этом выражение тепловой мощности справедливо только на участке нагревателя.

В случае участка источника произведение называется мощностью источника.

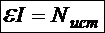
Теперь мы можем легко записать соотношение мощностей на участке источника:

Þ

Þ .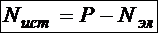

Если электрическая мощность участка Nэл равна скорости потребления участком механической энергии носителей, то , наоборот, равна скорости передачи энергии от участка носителям. Значит, энергия, вырабатываемая источником положительной ЭДС в единицу времени, частично поглощается на самом участке источника и выделяется в виде тепла, а её остаток в виде механической энергии носителей уходит за пределы участка. Очевидно, это закон сохранения энергии на участке источника.

Законом Джоуля-Ленца можно назвать всю совокупность выражений мощностей, связанных с электрическим током: тепловой, электрической, потребителя и источника. Таким образом, умножая почленно закон Ома на силу тока, мы приходим к закону Джоуля-Ленца. Этот закон является самым важным с практической точки зрения законом теории тока. Ведь из него понятно, зачем нужен электрический ток: для того, чтобы донести энергию от источников потребителям.

§17.10. Закон Джоуля-Ленца в дифференциальной форме

Рассмотрим скалярное произведение плотности тока на напряжённость движущей силы:

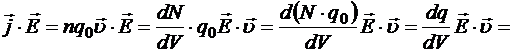
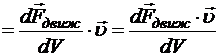
Выражение 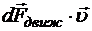, стоящее в числителе, представляет собой мощность электрических и сторонних сил, имеющую место в элементарном объёме проводника dV. Следовательно, скалярное произведение представляет собой объёмную плотность мощности этих сил.

В стационарном случае заряд dq находится в равновесии, а значит, элементарная работа и мощность его равнодействующей равна 0. Следовательно, мощность движущей силы по модулю равна мощности силы сопротивления, то есть тепловой мощности. Итак, объёмная плотность движущей силы равна объёмной плотности тепловой мощности.

Вспомним закон Ома в дифференциальной форме: 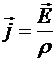. Умножим скалярно обе части этого равенства на вектор :

.

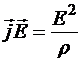Поскольку, в левой части стоит объёмная плотность мощности движущей силы, то правая часть представляет собой объёмную плотность тепловой мощности. Её можно выразить также через плотность тока и удельное сопротивление, используя выражение напряжённости из дифференциального закона Ома: Итак, мы получили выражение объёмной плотности тепловой мощности в случае стационарного поля плотности тока: