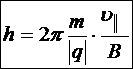| Магнитное поле и его воздействие на движущиеся заряды

Тогда молярная теплоёмкость кристаллической решётки

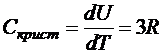Последнее соотношение называется законом Дюлонга-Пти.

Как видно из §18.3, молярная теплоёмкость электронного газа

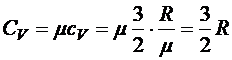Таким образом, молярная теплоёмкость металлов должна быть

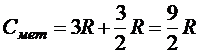Эксперименты же показывают, что

теплоёмкость металлов при комнатных и выше температурах определяется законом Дюлонга-Пти.

Это означает, что классическое предсказание теплоёмкости электронного газа сильно завышено.

В рамках классической теории противоречия пп. 18.4.1, 18.4.2, 18.4.3 неустранимы. И только квантовая теория металлов позволяет правильно рассчитать удельное сопротивление, длину свободного пробега и электронную теплоёмкость.

Относительно правильное значение постоянной Видемана-Франца

получилось потому, что две ошибки скомпенсировали друг друга:

во сколько раз предсказанная теплоёмкость оказалась завышенной по сравнению с реальной, во столько же раз теоретическое значение квадрата средней скорости теплового движения оказалось заниженным.

Глава 19. МАГНЕТИЗМ. МАГНИТНОЕ ПОЛЕ И ЕГО ИСТОЧНИКИ

§19.1. Магнитное поле и его воздействие на движущиеся заряды

Многочисленные опыты показали, что вокруг движущихся зарядов кроме электрического поля существует ещё одно, которое назвали магнитным. Характерной его особенностью является то, что оно действует только на заряды, имеющие скорость. Таким образом, с помощью магнитного поля осуществляется взаимодействие движущихся зарядов. Если хотя бы один из двух взаимодействующих зарядов неподвижен, то взаимодействие между ними — только электростатическое.

Математически физическое магнитное поле представляется как векторное поле магнитной индукции . Линия магнитного поля, как и электрического, называется силовой, но в отличие от электрической напряжённости магнитная индукция не является силой, действующей на единичный пробный заряд. Сила, действующая со стороны магнитного поля на заряд, движущийся в нём, определяется с помощью вектора по закону, полученному опытным путём:

,

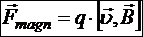здесь q — значение движущегося заряда, — его скорость, — магнитная индукция в месте нахождения заряда.

Единица измерения магнитной индукции в СИ называется теслой (Тл).

Очевидно, что однородным называется поле, вектор которого одинаков во всём пространстве. Также как и электрическое, однородное магнитное поле изображается с помощью эквидистантных силовых линий.

Очевидно, что на заряд, движущийся параллельно вектору , магнитная сила не действует. Из формулы магнитной силы следует, что она перпендикулярна скорости заряда. Следовательно, её мощность равна 0, следовательно, она не совершает работы, следовательно, если частица движется только под действием магнитной силы, то кинетическая энергия, а значит, и величина скорости частицы неизменны.

Рассмотрим движение заряженной частицы в однородном магнитном поле (рис.19.1). Разложим скорость частицы на перпендикулярную и параллельную магнитному полю составляющие:

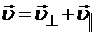
Тогда

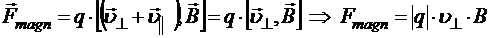
Поскольку ускорение , испытываемое частицей, также как и вектор , лежит в плоскости, перпендикулярной вектору ,

Рис.19.1

то движение, связанное с перпендикулярной составляющей скорости, представляет собой движение в плоскости, перпендикулярной магнитному полю с неизменным модулем скорости . В соответствие со вторым законом Ньютона

,

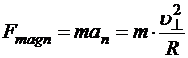где R — радиус кривизны плоской траектории. Тогда в случае однородного магнитного поля

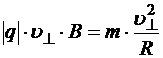Þ ,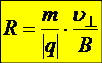

мы получили неизменную величину, следовательно, частица движется по окружности. Период обращения по этой окружности

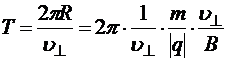Þ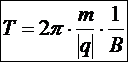

Циклическая частота

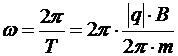Þ .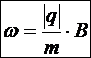

Все параметры вращательного движения содержат выражение удельного заряда частицы .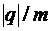

Учёт продольной скорости приведёт к наложению на движение по окружности равномерного движения в направлении поля. Траектория в этом случае будет представлять собой винтовую спираль с постоянным шагом

Þ

§19.2. Релятивистская природа магнитного воздействия

При совместном воздействии электрического и магнитного полей к заряду приложена сила, которая называется силой Лоренца:

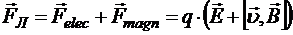
В нерелятивистском приближении, справедливом при скоростях движения, значительно меньших скорости света, сила, действующая на тело, не должна зависеть от выбора инерциальной системы отсчёта (ИСО). Между тем, магнитная составляющая силы Лоренца зависит от этого выбора. Поэтому при смене ИСО должна изменяться и электрическая составляющая, так чтобы полная сумма не изменилась. Таким образом, разделение силы Лоренца на магнитную и электрическую составляющие является относительным, то есть зависит от выбора ИСО.

При переходе от одной ИСО к другой меняется не только скорость частицы, но и поля: как электрическое, так и магнитное.

Проиллюстрируем это утверждение на самом простом примере взаимодействия частицы (например, электрона) и равномерно заряженной плоскости неподвижных относительно друг друга (рис.19.2). В системе, где пластина и электрон неподвижны (а), сила взаимодействия только электростатическая и на электрон действует сила 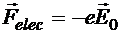, где 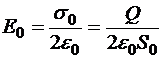. В ИСО, где плоскость и электрон около неё движутся (б) возникает магнитная составляющая взаимодействия, для электрона − отталкивающая (как будет объяснено позже). Значит, для компенсации должна увеличиться сила электрического приближения, то есть должна стать более сильной напряжённость электрического поля , следовательно, должна увеличиться поверхностная плотность заряда s‘.

Рис.19.2

Это происходит благодаря релятивистскому сокращению размера пластины, продольного по скорости: