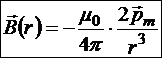Закон Био-Савара-Лапласа

Если частицы будут двигаться антипараллельно, то при остальных равных условиях разноимённые частицы будут притягиваться, а одноимённые будут отталкиваться также в соответствие с III-им законом Ньютона.

Но в общем случае III-й закон Ньютона выполняться не будет:

Рис.19.7

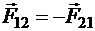, но линии действия этих сил не совпадают. Есть пример ещё более красноречивый:

Рис.19.8

В этом случае .

Дело в том, что III-й закон Ньютона является частным случаем закона сохранения импульса замкнутой системы. Импульс системы двух движущихся зарядов не сохраняется, поскольку она не является замкнутой. Таковой является система «заряды+электромагнитное поле». Импульс электромагнитного поля компенсирует несохранение импульса частиц.

§19.7. Закон Био-Савара-Лапласа

По принципу суперпозиции магнитные поля движущихся частиц векторно складываются, причём каждый заряд возбуждает поле, не зависящее от наличия других источников. Следовательно, магнитное поле, созданное элементом объёма dV проводника с током, равно сумме магнитных полей каждого носителя, находящегося в этом объёме. Поскольку, все носители одинаковы, имеют общую скорость и находятся в одной точке, то общее поле

,

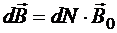где 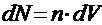— общее количество носителей, — поле одного носителя. То есть,

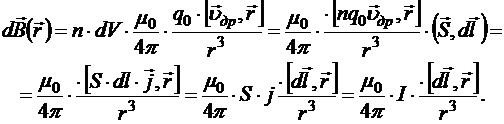
Рис.19.9

Полученная формула и есть закон Био-Савара-Лапласа, то есть соотношение, описывающее магнитную индукцию, созданную элементом проводника с током I (рис.19.9):

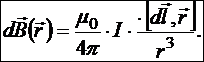
§19.8. Простейшие примеры применения закона Био-Савара-Лапласа

19.8.1. Магнитное поле прямолинейного проводника с током.

Рис.19.10

Для всех элементов рассматриваемого на рисунке 19.10 участка прямолинейного проводника с током направление элементарного вклада в общий вектор магнитной индукции – одинаково (перпендикулярно плоскости рисунка от нас). Следовательно, для подсчёта модуля вектора в точке А В(А) достаточно учитывать только модули элементарных вкладов

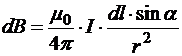
Из дополнительного рисунка видно, что

.

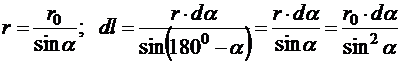Следовательно,

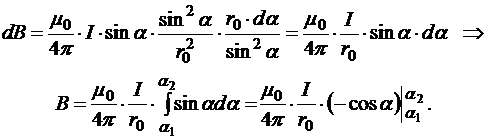
Окончательно:

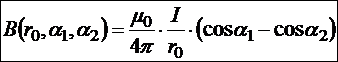
В случае бесконечно длинного проводника

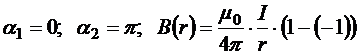Þ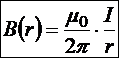

Силовая линия представляет собой окружность, концентрическую с проводником, направление вектора магнитной индукции будет соответствовать правилу правого винта:

Рис.19.11

19.8.2. Взаимодействие двух бесконечно длинных прямых параллельных токов

Рис.19.12

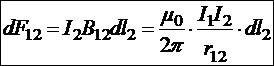
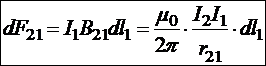
Этими формулами пользуются для определения единицы измерения тока.

19.8.3. Магнитное поле кругового витка с током в центре витка

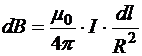; Þ

Þ .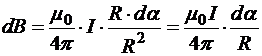

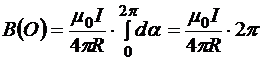, следовательно,

.

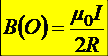19.8.4. Магнитное поле кругового витка с током на произвольной точке оси, перпендикулярной витку и проходящей через его центр

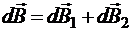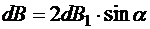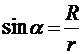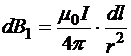; ; ; Þ

Þ .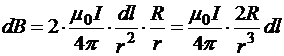

Рис.19.14

Поскольку dB создан двумя диаметрально противоположными элементами dl, то интегрирование нужно производить по половине окружности. Следовательно,

.

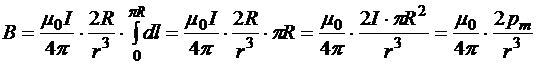С учётом направления:

;

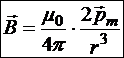при .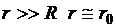

19.8.5. Магнитное поле кругового витка с током в произвольной точке плоскости витка, удалённой от витка

Рис.19.15

При векторы 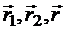параллельны друг другу, следовательно, линии диаметрально противоположных элементарных участков витка 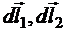пересекают их под одинаковым углом a. По закону БСЛ:

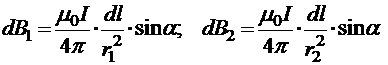
Они направлены антипараллельно, то есть

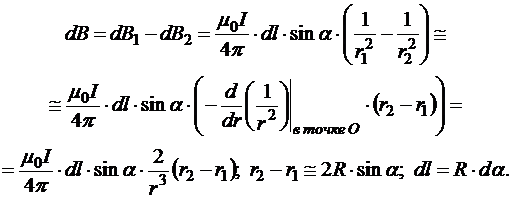
После подстановки получаем:

.

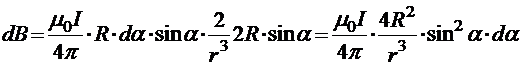Точно так же, как и в предыдущем пункте, интегрировать нужно по половине окружности, следовательно,

.

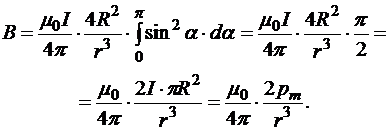Из рисунка видно, что