Теорема Остроградского-Гаусса для магнитного поля

Контрольные вопросы к главе 19

1. Какое время должен затратить протон в магнитном поле циклотрона, чтобы приобрести кинетическую энергию 10 МэВ, если при каждом обороте протон проходит между дуантами разность потенциалов 30 кВ? Магнитное поле циклотрона равно 1 Тл. (Ответ: »3,47 мкс) (§19.1)

2. Тонкое металлическое кольцо быстро вращается вокруг вертикальной оси, проходящей через его диаметр и перпендикулярной однородному магнитному полю с индукцией 10-2 Тл. Пренебрегая трением в оси, определите, через какое время угловая скорость вращения уменьшается в е раз. (Ответ: »7,2 с) (§19.1)

3. По тонкому проводу в виде кольца радиусом 20 см течёт ток 100 А. Перпендикулярно плоскости кольца возбуждено однородное магнитное поле с индукцией 20 мТл. Чему равна сила, растягивающая кольцо? (Ответ: 0,4 Н) (§19.3)

4. На оси контура с током, магнитный момент которого равен 10 мА×м2, находится такой же контур. Вектор магнитного момента второго контура перпендикулярен оси. Чему равен механический момент, действующий на второй контур? Расстояние между контурами равно 50 см. Размеры контуров малы по сравнению с расстоянием между ними. (Ответ: »0,16 нН×м) (§19.4)

5. Как будет себя вести изначально неподвижный магнитный момент, направленный по полю в представленном на рисунке магнитном поле? (Ответ: ускоренно двигаться влево) (§19.4)

6. Выполняется ли третий закон Ньютона при магнитном взаимодействии точечных зарядов? Возможна ли ситуация, когда первый заряд на второй действует, а второй на первый нет? (§19.5)

7. Какова степень расстояния между источником и точкой наблюдения в зависимости модуля магнитной индукция от точки наблюдения? (§19.7)

8. Магнитный момент, равный 1 А×м2, помещён в центр плоской петли радиуса 10 см на бесконечно длинном тонком проводе с силой тока 50 А, такой как показано на рисунке. Чему равен механический момент, действующий на магнитный? (Ответ: »214 мкН×м) (§19.8)

9. Магнитный момент, равный 1 А×м2, помещён в центр плоской петли радиуса 10 см на бесконечно длинном тонком проводе с силой тока 50 А, такой как показано на рисунке. Чему равен механический момент, действующий на магнитный? (Ответ: »414 мкН×м) (§19.8)

10. Магнитные моменты из двух предыдущих задач перенесли на 5 метров из центров петель перпендикулярно проводу вверх. На сколько будут отличаться механические моменты первого и второго магнитного момента в новом положении? (Ответ: второй больше первого на »5нН×м) (§19.8)

Глава 20. МАГНЕТИЗМ. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ

§20.1. Теорема Остроградского-Гаусса для магнитного поля

Магнитным потоком Фm называется поток вектора магнитной индукции.

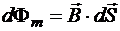
Теорема Остроградского-Гаусса для магнитного потока является обобщением опытных фактов:

магнитный поток через любую замкнутую поверхность равен 0.

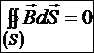
Это означает, что силовые линии магнитного поля замкнуты, и в природе не существует магнитных зарядов — источников магнитного поля, из которых могли бы исходить силовые линии или на которых они обрывались бы. Источниками магнитного поля являются токи, и силовые линии магнитного поля замыкаются вокруг них.

§20.2. Работа силы Ампера на перемещении проводника с током в постоянном магнитном поле

Рассмотрим элемент с током , ориентированный по току, движущийся со скоростью в постоянном магнитном поле с индукцией в месте нахождения . На один носитель заряда q0 в этом элементе со стороны магнитного поля действует сила, равная

,

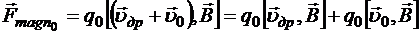где — дрейфовая скорость носителей относительно элемента .

Полная сила, действующая со стороны магнитного поля на совокупность носителей заряда в рассматриваемом элементе с током:

,

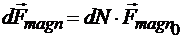где dN — количество носителей в элементе. Тогда

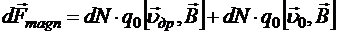
С первым слагаемым мы уже сталкивались. Это — сила Ампера 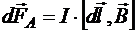. Последнее слагаемое обозначим , то есть

.

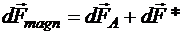Пусть dt — время, которое один носитель затрачивает на прохождение отрезка движущегося проводника. Тогда 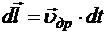представляет собой перемещение всех рассматриваемых dN носителей относительно движущегося проводника. Обозначим элементарное перемещение проводника с током за время dt относительно неподвижного магнитного поля, как . Полное перемещение совокупности dN носителей относительно источников постоянного магнитного поля в соответствие с классической относительностью перемещения

.

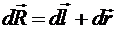Следовательно, работа магнитной силы на перемещении совокупности dN носителей

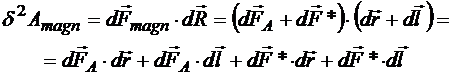
формально раскладывается на 4 слагаемых. Теперь проанализируем ситуацию с направлениями. Очевидно, что 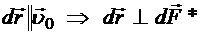, поскольку 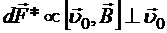. Очевидно, что 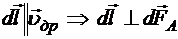, поскольку 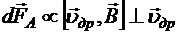(рис.20.1).

Рис.20.1

Значит, из четырёх слагаемых элементарной работы магнитной силы два, и 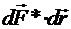, равны 0. Оказывается, эта работа содержит всего два слагаемых:

.

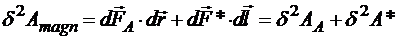Рассмотрим эти слагаемые по очереди.

Элементарная работа силы Ампера, действующей на элемент проводника с током

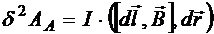
выражается через смешанное произведение трёх векторов, к которому применимо правило циклической перестановки:

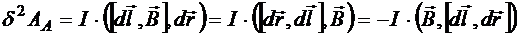
Вектор является вектором элементарной площади, заметённой элементом при его поступательном движении (рис.20.2, левый).