МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ

Глава 21. МАГНЕТИЗМ. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ

§21.1. Орбитальные моменты

Согласно представлениям классической физики электроны в атомах движутся по замкнутым траекториям — орбитам, образуя систему замкнутых орбитальных токов. Наиболее простой вариант реализации этой модели — вариант круговых орбит. Мы будем рассматривать только такие орбиты.

Движение электрона по круговой орбите радиуса r с периодом Т создаёт орбитальный ток, сила которого

,

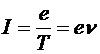где n — частота вращения. Орбитальному току соответствует магнитный момент, модуль которого

,

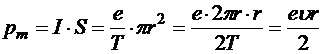где 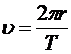— величина скорости электрона на орбите. Поскольку заряд электрона отрицательный, его орбитальная скорость направлена против направления орбитального тока.

Из механики известно, что вращение массы по круговой орбите характеризуется моментом импульса, который в нашем случае будет называться орбитальным моментом импульса электрона:

.

Здесь — импульс электрона, связанный с его орбитальным движением. Как известно, направление угловой скорости связано с линейной скоростью по правилу правого винта. С другой стороны, направление орбитального магнитного момента по правилу правого винта связано с направлением орбитального тока. А поскольку ток и линейная скорость направлены противоположно друг другу, то направления и также противоположны. На рисунке 21.2 изображена электронная орбита со всеми векторными и скалярными величинами, о которых шла речь выше.

Радиус-вектор электрона на круговой орбите всегда направлен перпендикулярно линейной скорости, поэтому модуль орбитального момента импульса 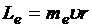. Уже упоминалось, что величина магнитного момента . Отсюда с учётом направлений мы можем написать векторное равенство

.

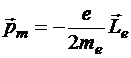Коэффициент, связывающий орбитальный магнитный момент и орбитальный момент движения электрона, называется гиромагнитным отношением электронной орбиты g.

, где .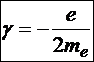

Орбитальным магнитным моментом атома называется векторная сумма орбитальных магнитных моментов отдельных электронов:

,

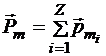где Z — число электронов в атоме.

Орбитальный момент импульса атома равен векторной сумме орбитальных моментов импульса отдельных электронов:

.

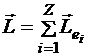Легко показать, что орбитальный магнитный момент атома связан с атомным моментом движения через гиромагнитное отношение электронной орбиты:

.

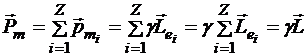Ядра атомов также имеют магнитные моменты, но, как правило, они на несколько порядков меньше, чем атомные орбитальные магнитные моменты, и мы их учитывать не будем.

§21.2. Классический атом в магнитном поле

На электронную орбиту (орбитальный магнитный момент), помещённую в магнитное поле действует момент сил

.

Согласно основному уравнению динамики вращательного движения

.

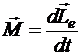Заменяя левую часть предпоследнего равенства, получаем дифференциальное уравнение относительно :

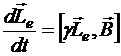или .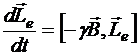

Переписанное таким образом дифференциальное уравнение полностью совпадает с дифференциальным уравнением радиус-вектора , вращающегося с угловой скоростью . Оно рассматривалось в курсе механики (кинематика вращательного движения):

.

Поэтому легко сделать вывод, что под влиянием магнитного поля вектор совершает вращательное движение с угловой скоростью

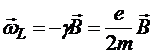
вокруг оси, направленной по вектору магнитной индукции (рис.21,2). Понятно, что из всех «траекторий», изображённых на рисунке в реальном пространстве существует только орбита электрона, помеченная орбитальным током I.

Вращательное движение орбитальных моментов и означает вращение плоскости орбиты, то есть прецессию. Таким образом, мы доказали теорему Лармора:

единственным результатом влияния магнитного поля на орбиту электрона в атоме является прецессия орбиты и вектора с угловой скоростью вокруг оси, проходящей через ядро атома и параллельной вектору .

Понятно, что прецессия орбиты, создавая дополнительное к орбитальному движение заряда, создаёт и дополнительный орбитальный ток DI, и дополнительный орбитальный магнитный момент (рис.21.3). Значение дополнительного орбитального тока определяется из выражения, аналогичного выражению основного орбитального тока:

.

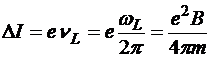Из рисунка видно, что направление дополнительного орбитального магнитного момента одного электрона противоположно . Отсюда понятно, что и весь наведённый в магнитном поле момент атома будет направлен против наводящего магнитного поля.

§21.3. Классификация веществ по их магнитным свойствам

Все среды при рассмотрении их магнитных свойств называются магнетиками. Модельное понятие среды обсуждалось раньше, в частности, в главе «Электрическое поле в диэлектрической среде». Дальнейшее изложение будет во многом аналогично изложению указанной темы из электростатики. Поэтому многие теоретические подробности перехода от классических микроскопических моделей к макроскопическим характеристикам среды здесь будут опущены.