Диамагнетики
Всякая среда при внесении её во внешнее магнитное поле изменяет своё магнитное состояние. Количественной характеристикой магнитного состояния среды служит намагниченность , магнитный момент её единицы объёма.
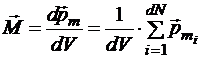 .
.
Здесь dV — элементарный с макроскопической точки зрения объём магнетика, в котором содержится dN~NA атомных магнитных моментов ![]() , создающих суммарный дипольный момент
, создающих суммарный дипольный момент ![]() .
.
Намагниченность можно выразить через концентрацию атомных магнитных моментов n и средний по объёму dV атомный магнитный момент 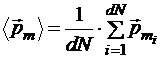 :
:
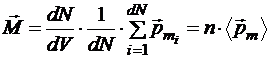
По своим магнитным свойствам магнетики подразделяются на три основных группы: диамагнетики, парамагнетики и нелинейные магнетики. Из представителей последней группы мы будем рассматривать только ферромагнетики.
§21.4. Диамагнетики
Именно к диамагнетикам иногда количественно, а чаще качественно приложима теория Лармора, так как это — среды, которые в отсутствие внешнего магнитного поля имеют нулевую намагниченность, а во внешнем магнитном поле намагничиваются против него. К диамагнетикам относятся инертные газы, щёлочно-галоидные соединения (например, поваренная соль NaCl), многие металлы (например, Bi, Ag, Au, Cu), большинство органических соединений, углерод, смолы.
Между электрическими свойствами диэлектриков и магнетиками всегда можно провести аналогию. В этом смысле диамагнетики аналогичны неполярным диэлектрикам, поскольку в отсутствие внешнего магнитного поля атомные моменты диамагнетиков равны 0. При внесении во внешнее магнитное поле атомы диамагнетиков приобретают наведённые магнитные моменты ![]() , направленные, согласно теории Лармора, против индуцирующего их внешнего магнитного поля.
, направленные, согласно теории Лармора, против индуцирующего их внешнего магнитного поля.
§21.5. Парамагнетики
Эти среды также как и диамагнетики в отсутствие внешнего магнитного поля обладают нулевой намагниченностью, но в отличие от диамагнетиков намагничиваются в направлении внешнего магнитного поля. На микроскопическом уровне парамагнетики отличаются от диамагнетиков наличием собственного (ненаведённого) магнитного момента у одной микрочастицы вещества. В аналогии между диэлектриками и магнетиками парамагнетики стоят против полярных диэлектриков.
Само существование парамагнетиков уже не укладывается в классические рамки, поскольку противоречит теореме Лармора. Но, приняв без объяснения факт их существования, классическая теория трактует намагничивание парамагнетиков как результат ориентирующего воздействия магнитного поля на неизменный по величине магнитный момент атома парамагнетика, подобно тому, как магнитное поле Земли ориентирует магнитную стрелку компаса. Классическая теория намагничивания парамагнетиков, также как и поляризации полярных диэлектриков, разработана Ланжевеном. В главе «Магнитное поле и его источники» было показано, что потенциальная энергия магнитного момента ![]() в магнитном поле
в магнитном поле
![]() .
.
Точно также и энергия дипольного электрического момента ![]() в электрическом поле:
в электрическом поле:
![]() .
.
Теория Ланжевена основана на независимости друг от друга отдельных микроскопических моментов (на отсутствии их взаимодействия). Тогда можно статистически рассматривать только один микроскопический момент из множества одинаковых, вычисляя вероятности различных ориентаций неизменного по модулю момента в постоянном магнитном поле с индукцией ![]() .
.
Согласно распределению Больцмана, о котором говорилось во время рассмотрения полярных диэлектриков, малые углы между моментом и полем более вероятны. Следовательно, во внешнем поле магнитные моменты парамагнетика с большей вероятностью ориентированы по полю.
Теория намагничивания полностью повторяет теорию поляризации полярного диэлектрика, конечную формулу которой мы здесь приводим:
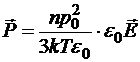 .
.
Для того, чтобы получить формулу намагниченности достаточно заменить поляризацию ![]() на намагниченность , дипольный момент
на намагниченность , дипольный момент ![]() на магнитный момент
на магнитный момент ![]() , а напряжённость электрического поля
, а напряжённость электрического поля ![]() на магнитную индукцию
на магнитную индукцию ![]() . Кроме этого, константу e0 в знаменателе нужно заменить на константу m0 в числителе, но в данном случае замена числителя на знаменатель ничего не меняет. В результате:
. Кроме этого, константу e0 в знаменателе нужно заменить на константу m0 в числителе, но в данном случае замена числителя на знаменатель ничего не меняет. В результате:
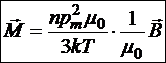
при условии 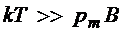 .
.
Если ввести безразмерный параметр 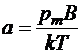 , то выражение модуля намагниченности во всём диапазоне полей и температур, сохраняющих парамагнитный свойства образца, может быть записано в виде:
, то выражение модуля намагниченности во всём диапазоне полей и температур, сохраняющих парамагнитный свойства образца, может быть записано в виде:
![]() .
.
Здесь L(а) — безразмерная функция Ланжевена, график которой имеет вид:
 Рис.21.4
Рис.21.4
При а>>1 L(a)»1 (режим магнитного насыщения); при a<<1 L(a) прямо пропорциональна a/3 (получено).
§21.6. Магнитная восприимчивость
В полной аналогии с формулой поляризации диэлектрика
![]() ,
,
где c — безразмерная диэлектрическая восприимчивость вещества, можно записать соотношение:
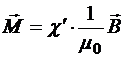 .
.
Здесь ![]() — магнитная индукция внутри магнетика (обратите внимание, что это поле, созданное и внешними по отношению к магнетику источниками, и самим магнетиком). В случае диамагнетика
— магнитная индукция внутри магнетика (обратите внимание, что это поле, созданное и внешними по отношению к магнетику источниками, и самим магнетиком). В случае диамагнетика ![]() ; в случае парамагнетика при малых значениях параметра Ланжевена а
; в случае парамагнетика при малых значениях параметра Ланжевена а 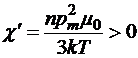 ,
, ![]() . То есть во всех случаях
. То есть во всех случаях ![]() .
.
По исторически сложившейся традиции в качестве магнитной восприимчивости магнетика используется не ![]() , а c, связанное с
, а c, связанное с ![]() соотношением
соотношением
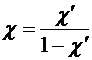 .
.
И для диамагнетиков, и для парамагнетиков ![]() . Причём, эта величина не зависит от магнитной индукции. Поэтому такие магнетики называются линейными. Таким образом, запомним, что в случае парамагнетиков при малых магнитных полях и высоких температурах
. Причём, эта величина не зависит от магнитной индукции. Поэтому такие магнетики называются линейными. Таким образом, запомним, что в случае парамагнетиков при малых магнитных полях и высоких температурах
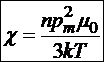 .
.
§21.7. Закон полного тока в магнетике
При изучении магнитного поля в веществе (магнетике) различают два типа токов: макро и микротоки. Под макротоками понимают электрические токи проводимости, которые принято трактовать как токи свободного заряда. Микротоками или молекулярными токами называют токи, обусловленные движением заряда в атомах, ионах и молекулах.


