Ферромагнетики

Соответственно, в магнетике полное магнитное поле создаётся как макротоками, так и микротоками. Первая компонента полного магнитного поля называется внешним полем, магнитную индукцию которого мы будем обозначать , вторая — внутренним (). Итак, магнитная индукция в магнетике:

.

Следовательно, закон полного тока в магнетике можно записать так:

.

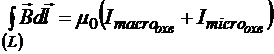Молекулярный ток одной микрочастицы свяжем с её магнитным моментом так:

,

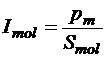где Smol — эффективная площадь «витка» молекулярного тока. Для определённого контура L вклад в 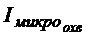дают только молекулярные токи, эффективные «витки» которых нанизаны на контур L как бусы на нитку.

Рис.21.5

На примере диамагнетика проиллюстрируем общее соотношение:

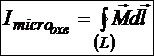
В диамагнетике все молекулярные магнитные моменты являются наведёнными, то есть направлены против магнитной индукции. Ясно, что мы рассматриваем случаи, когда неоднородности магнитного поля имеют макроскопические размеры, также как и пространственные дифференциалы. Это значит, что на протяжении элементарного участка замкнутого контура L магнитное поле можно считать однородным. Следовательно, все молекулярные магнитные моменты, находящиеся вблизи , направлены в одну сторону и одинаковы по величине. А значит, . На элемент нанизаны молекулярные токи всех N микрочастиц, находящихся в объёме косого цилиндра, показанного на рис.21.6.

Рис.21.6

,

Тогда малому элементу dl контура соответствует охватываемый контуром микроток:

.

Следовательно,

.

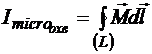Тогда циркуляция вектора по произвольному контуру L в магнетике

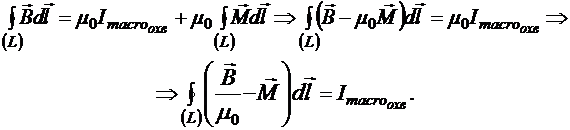
Введём по определению вектор напряжённости магнитного поля:

,

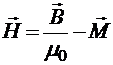физическая размерность которой совпадает с размерностью (А/м). Тогда мы можем записать закон полного тока для магнетика через циркуляцию :

.

В случае, если макроток непрерывно распределён по поверхности, натянутой на контур, мы имеем теорему Стокса для магнитной среды:

.

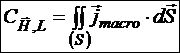Из этих формул видно, что векторное поле напряжённости определяется внешними по отношению к магнетику источниками. Поэтому поле напряжённости называется внешним полем. Таким образом, магнитное поле во всех средах характеризуется двумя векторными величинами: напряженностью и магнитной индукцией . В вакууме физическое содержание этих двух векторов полностью совпадает, поскольку здесь они связаны посредством магнитной постоянной вакуума m0, которая, будучи мировой константой, не изменяется ни при каких обстоятельствах:

.

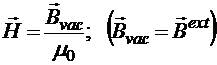Но «дублирование» прекращается, когда место вакуума замещается магнетиком. характеризует поле «само по себе», учитывая влияние только источников и не включая в себя влияние среды. В отсутствие влияния поверхности магнетика напряжённость в магнетике полностью совпадает с напряжённостью в вакууме на месте магнетика, если его удалить. В противоположность этому несет в себе информацию о «поле в веществе».

Поскольку ,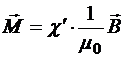

.

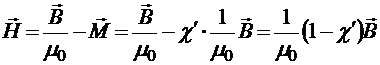По определению введём магнитную проницаемость магнетика — безразмерную величину, являющуюся характеристикой среды:

.

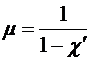Тогда получаем самую употребляемую формулу связи двух характеристик магнитного поля:

.

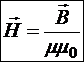Используя соотношение 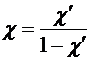, выразим через :

.

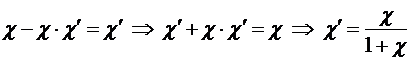Тогда

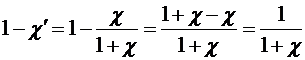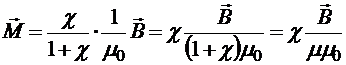Þ .

Þ .

Сейчас мы запишем все возможные выражения магнитной индукции:

.

Последние три выражения показывают, как изменяется магнитная индукция поля источников при замещении вакуума на магнетик, и что является причиной этого изменения. Слагаемое

называется откликом среды на внешнее поле.

§21.8. Ферромагнетики

Характерной особенностью диамагнетиков и парамагнетиков является то, что их магнитная восприимчивость не зависит от внешнего поля . Поэтому эти магнетики называются линейными. С микроскопической точки зрения можно сказать, что магнитные моменты микрочастиц линейных магнетиков (наведённые или уже существующие) не взаимодействуют друг с другом по причине сравнительно малых значений этих моментов. Но кроме линейных магнетиков есть магнетики со значительными магнитными моментами частиц. Для них характерно сильное взаимодействие между отдельными микроскопическими моментами. Природа этого взаимодействия отнюдь не проста и не сводится к хорошо известному притягиванию разных полюсов магнитов друг к другу. На самом деле, наиболее существенное слагаемое магнитного взаимодействия имеет квантовомеханическую природу. Для нас сейчас важно то, что величина его прямо пропорционально зависит от произведения взаимодействующих моментов. Поэтому-то в линейных магнетиках, где величина микроскопических магнитных моментов невелика, энергия взаимодействия между ними мала по сравнению с энергией тепловых возбуждений kT вплоть до самых низких температур. В результате атомные моменты при любых температурах «не чувствуют» друг друга.