Замыкание и размыкание электрической цепи

,

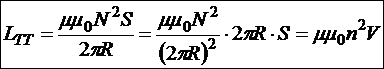где 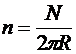— плотность намотки витков на тороид; — объем полости тороида. Последняя форма записи позволяет использовать ее для выражения индуктивности длинного соленоида:

.

В этом случае объём полости соленоида V=lS, где l – длина соленоида ().

Итак: 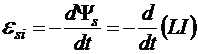, следовательно,

.

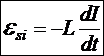Знак «минус», соответствующий правилу Ленца, показывает, что ЭДС самоиндукции препятствует изменению тока в контуре. «Интенсивность» этого препятствования изменениям характеризуется параметром L. Таким образом, индуктивность – мера инертности контура по отношению к изменениям силы тока в нем.

Для ферромагнетиков можно написать аналогичное по форме выражение:

,

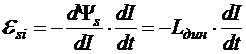где динамическая индуктивность контура .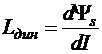

§22.3. Замыкание и размыкание электрической цепи

По закону Ома для замкнутой цепи с общим сопротивлением R (включающим и внутреннее сопротивление гальванических элементов) 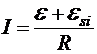, где e — ЭДС гальванических элементов.

Следовательно,

.

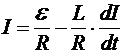Для того чтобы определить временное поведение тока в контуре нужно решить это дифференциальное уравнение.

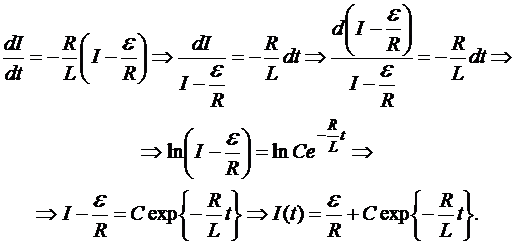
Константа С находится из начальных условий. Замыкание цепи: I(0)=0, то есть 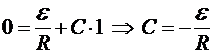. Следовательно, ток замыкания:

.

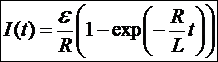Рис.22.1

На рисунке введено обозначение: .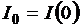

Ток размыкания возникает, когда отключаются ЭДС гальванических элементов. В этом случае дифференциальное уравнение для силы тока примет вид:

,

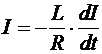где R — сопротивление цепи, по которой протекает ток размыкания. Простой метод разделения переменных приводит к соотношению дифференциалов:

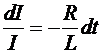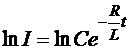Þ Þ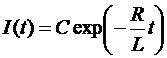

Ясно, что 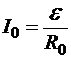, где R0 — сопротивление цепи до её размыкания. Тогда 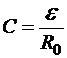. Следовательно,

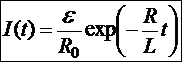
Рис.22.2

Время 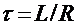, представленное на эпюрах токов замыкания и размыкания (рис.22.1, 22.2), называется временем релаксации. Его принято считать характерным временем переходного процесса в контуре.

§22.4. Энергия магнитного поля в неферромагнитной изотропной среде

Еще раз запишем закон Ома для мгновенного значения тока в цепи с самоиндукцией.

,

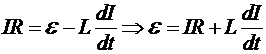где e — ЭДС внешних по отношению к контуру источников тока. Работа, dAстор, совершаемая внешними источниками за время dt,:

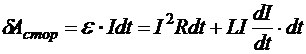
– джоулево тепло, которое источникам необходимо компенсировать для поддержания тока в контуре. Следовательно,

.

Проинтегрировав второе слагаемое в процессе включения тока, получим работу сторонних сил, необходимую для установления силы тока I в данном контуре:

.

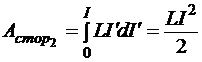Значит, ток, установившийся в данном контуре, обладает энергией

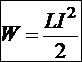
Далее, в качестве примера, иллюстрирующего общие соотношения, рассмотрим длинный соленоид:

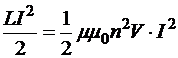. Поскольку 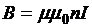, то 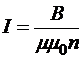, следовательно,

,

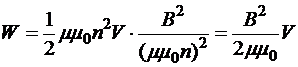то есть энергией обладает магнитное поле установившегося в контуре тока, и объемная плотность этой энергии

.

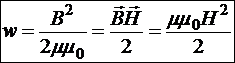При размыкании цепи магнитное поле тока рассасывается, а его энергия выделяется, как правило, в виде тепла во время протекания тока размыкания.

Контрольные вопросы к главе 22

1. На рисунке изображено вихревое электрическое поле в данном месте. Выберите все возможные варианты из предложенных? (§ 22.1)

а. Магнитное поле направлено на нас и не меняется с течением времени

б. Магнитное поле направлено на нас и увеличивается

в. Магнитное поле направлено на нас и уменьшается

г. Магнитное поле направлено от нас и увеличивается

д. Магнитное поле направлено от нас и уменьшается

е. Магнитное поле направлено параллельно плоскости рисунка и уменьшается

ж. Магнитное поле направлено параллельно плоскости рисунка и увеличивается

Глава 23. ЭЛЕКТРОДИНАМИКА. ОСНОВЫ ТЕОРИИ МАКСВЕЛЛА

(КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ)

§23.1. Введение

Электрическое и магнитное поле характеризуют в совокупности четыре векторных величины: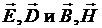. Зависимость от времени каждой из них определяется соответствующими дифференциальными уравнениями, которые при конкретных начальных и краевых условиях дают конкретные решения:

.

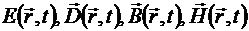Полная система дифференциальных уравнений, необходимых для описания поведения электрического и магнитного полей была получена Джеймсом Максвеллом в 60-х годах ХIX века.

При выводе уравнений Максвелла мы будем отталкиваться от интегральных соотношений, которые мы узнали в течение нашего курса. С помощью математических теорем интегральные соотношения будут сведены к дифференциальным. При этом нам понадобятся определенные знания из математической теории поля.

§23.2. Сведения из математической теории поля

23.2.1. Операции теории поля

а) Векторный дифференциальный оператор «набла»: