Теорема Гаусса
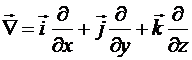 .
.
Все операции с ним выполняются по формальным правилам действий с векторами.
Например, операция «градиент» над скалярной функцией координат ![]() аналогична умножению вектора на скаляр:
аналогична умножению вектора на скаляр:
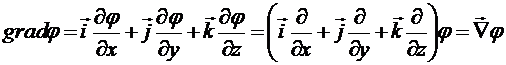
б) Операция «дивергенция» над векторным полем ![]() аналогична скалярному умножению векторов:
аналогична скалярному умножению векторов:
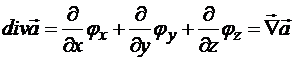 .
.
в) Операция «ротор» над векторным полем ![]() аналогична векторному умножению векторов:
аналогична векторному умножению векторов:
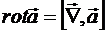 .
.
Поэтому чисто формально легко доказать, что
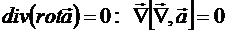 так как
так как ![]() ;
;
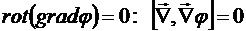 так как
так как 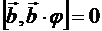 .
.
Если физический смысл операций «дивергенция» и «ротор» не очень понятен, то, надеемся, он станет понятен при изложении следующих математических теорем. Операция «градиент» подробно разъяснялась ранее, впрочем, она почти и не нужна сейчас.
23.2.2. Теорема Гаусса
Теорема Гаусса сводит поверхностный интеграл по замкнутой поверхности (S) к объемному интегралу по объему (V), охватываемому этой поверхностью.
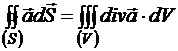
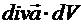 — это точечный источник расходящегося векторного поля или поток вектора
— это точечный источник расходящегося векторного поля или поток вектора ![]() через замкнутую поверхность, стянутую в точку. А теорема Гаусса – это всего лишь утверждение того факта, что поток через замкнутую поверхность равен сумме потоков из всех источников, заключенных внутри поверхности.
через замкнутую поверхность, стянутую в точку. А теорема Гаусса – это всего лишь утверждение того факта, что поток через замкнутую поверхность равен сумме потоков из всех источников, заключенных внутри поверхности.
23.2.3. Теорема Стокса
Теорема Стокса сводит криволинейный интеграл по замкнутому контуру (L), то есть циркуляцию, к поверхностному интегралу по поверхности (S), натянутой на этот контур.
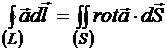 .
.
![]() — это вихрь поля в точке
— это вихрь поля в точке ![]() . Иными словами, это — вектор, перпендикулярный стянутому в точку контуру, в плоскости которого лежит вектор
. Иными словами, это — вектор, перпендикулярный стянутому в точку контуру, в плоскости которого лежит вектор ![]() и вдоль которого он циркулирует (рис.23.1). Его направление соответствует правилу правого винта, а модуль равен циркуляции
и вдоль которого он циркулирует (рис.23.1). Его направление соответствует правилу правого винта, а модуль равен циркуляции ![]() по этому контуру, нормированной на площадь поверхности, натянутой на контур. Тогда
по этому контуру, нормированной на площадь поверхности, натянутой на контур. Тогда ![]() — циркуляция поля по контуру поверхности
— циркуляция поля по контуру поверхности ![]() .
.
 Рис.23.1
Рис.23.1
Теорема Стокса – это утверждение того, что циркуляция по замкнутому контуру равна сумме циркуляций по всем внутренним областям охваченной поверхности. Рисунок 23.2 иллюстрирует смысл утверждения в самом простом и доходчивом случае: поверхность S состоит из одинаковых площадей ![]() с одинаковой циркуляцией и оконтурена периметром L.
с одинаковой циркуляцией и оконтурена периметром L.
 Рис.23.2
Рис.23.2
При суммировании циркуляций контурные интегралы по границам смежных областей взаимно уничтожаются.
23.2.4. Виды векторных полей
Из множества векторных полей выделяются два типа: потенциальные и вихревые.
Любое потенциальное векторное поле ![]() порождается операцией «градиент» над определённым скалярным полем. То есть существует такое скалярное поле
порождается операцией «градиент» над определённым скалярным полем. То есть существует такое скалярное поле ![]() , что
, что 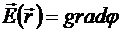 . Но тогда
. Но тогда
ротор потенциального поля равен 0.
Любое вихревое векторное поле ![]() порождается операцией «ротор» над определённым векторным полем. То есть существует такое векторное поле
порождается операцией «ротор» над определённым векторным полем. То есть существует такое векторное поле ![]() , что
, что 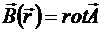 . Но тогда
. Но тогда
дивергенция вихревого поля равна 0.
§23.3. Система уравнений Максвелла
Запишем сразу всю систему уравнений в традиционном порядке:

Порядок записи максимально подчеркивает симметричность уравнений по отношению к электрическому и магнитному полю. При переходе от электрического к магнитному полю место напряженности электрического поля ![]() занимает вектор напряжённости магнитного поля , а вместо электрического смещения (электрической индукции)
занимает вектор напряжённости магнитного поля , а вместо электрического смещения (электрической индукции) ![]() выступает вектор магнитной индукции
выступает вектор магнитной индукции ![]() . При этом важно помнить, что физические роли электрических и магнитных векторов, носящих одно название, антисимметричны. Напряжённость электрического поля
. При этом важно помнить, что физические роли электрических и магнитных векторов, носящих одно название, антисимметричны. Напряжённость электрического поля ![]() включает в себя влияние, как внешних источников (свободных зарядов), так и самой диэлектрической среды (связанных зарядов). Напряжённость магнитного поля включает в себя влияние только внешних источников (макроскопических токов). Электрическая индукция
включает в себя влияние, как внешних источников (свободных зарядов), так и самой диэлектрической среды (связанных зарядов). Напряжённость магнитного поля включает в себя влияние только внешних источников (макроскопических токов). Электрическая индукция ![]() включает в себя влияние только внешних источников (свободных зарядов). Магнитная индукция
включает в себя влияние только внешних источников (свободных зарядов). Магнитная индукция ![]() включает в себя влияние, как внешних источников (макроскопических токов), так и самой среды магнетика (молекулярных токов).
включает в себя влияние, как внешних источников (макроскопических токов), так и самой среды магнетика (молекулярных токов).
Эту систему необходимо дополнить материальными уравнениями, характеризующими электрические, магнитные и транспортные свойства среды. Для изотропных, несегнетоэлектрических, неферромагнитных и подчиняющихся закону Ома сред:
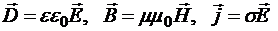 .
.
Выводить дифференциальные уравнения будем не в порядке записи, а в порядке возрастания сложности вывода и понимания.
§23.4. Четвертое уравнение Максвелла
Ранее была изложена теорема Остроградского-Гаусса для магнитного поля (тема «Интегральные уравнения магнетизма»):
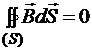 .
.
По математической теореме Гаусса 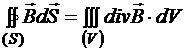 . Значит,
. Значит, 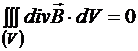 . Это справедливо для любого объема, в том числе и для бесконечно малого, следовательно,
. Это справедливо для любого объема, в том числе и для бесконечно малого, следовательно,
![]()


