Второе уравнение Максвелла

§23.5. Второе уравнение Максвелла

Ранее была доказана теорема Остроградского-Гаусса для электрического смещения электростатического поля в диэлектрической среде (тема «Электростатическое поле в диэлектрической среде»).

.

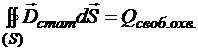С другой стороны очевидно, что .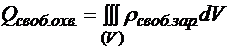

По математической теореме Гаусса

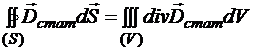Þ .

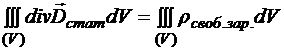Это справедливо для любого объема, в том числе и для бесконечно малого, следовательно,

Þ .

Полное электрическое смещение равно сумме смещений электростатического и вихревого полей:

,

следовательно,

.

§23.6. Первое уравнение Максвелла

В теме «Электромагнитная индукция» была получена формула:

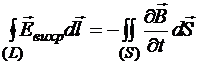
По математической теореме Стокса:

.

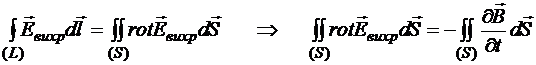Это справедливо для любой площади, в том числе и для бесконечно малой, следовательно,

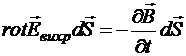, то есть, .

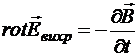Полная напряженность электрического поля

Из потенциальности электростатического поля следует Þ , следовательно,

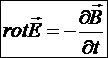
§23.7. Третье уравнение Максвелла

Вспомним теорему Стокса для магнитного поля в магнетике, выводившуюся в теме «Магнитное поле в веществе»:

.

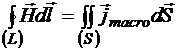По математической теореме Стокса

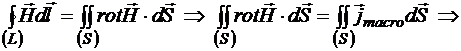
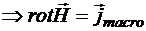
Вообще-то ранее мы определяли макроток как ток свободных зарядов. Но если считать, что всегда справедливо, то в случае нестационарного распределения заряда по пространству мы впадем в противоречие.

Взяв дивергенцию от обеих частей предыдущего равенства, получим с одной стороны:

.

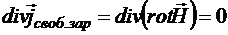Но с другой стороны из закона сохранения электрического заряда ясно, что если заряд внутри замкнутой поверхности меняется с течением времени, то

.

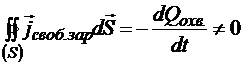Ясно, что по математической теореме Гаусса

,

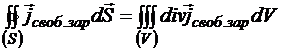а скорость истечения свободного заряда из замкнутой поверхности

.

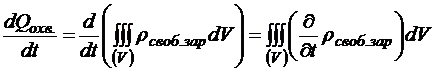Тогда:

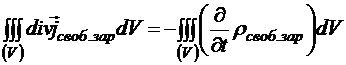
Отсюда получается, что в нестационарном случае

.

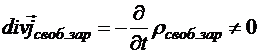Следовательно,

!!!!

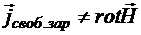Преобразуем предыдущее соотношение:

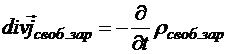Þ .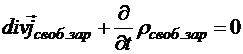

В соответствии со вторым уравнением Максвелла

,

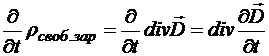так как смешанные частные производные можно брать в произвольном порядке. Следовательно:

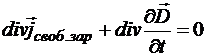Þ .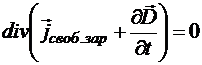

Максвелл решил считать, что в нестационарном случае

.

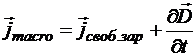Тогда противоречия не возникает.

Слагаемое Максвелл назвал током смещения, то есть

;

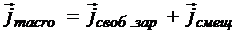Þ .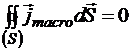

Получается, токи всегда замкнуты. Этот факт, очевидный для стационарных токов, с введением Максвеллом токов смещения распространяется и на нестационарные токи тоже. Например, ток разряда конденсатора замыкается током смещения внутри него.

Рис.23.3

Подставляя максвелловское определение плотности макроскопического тока в выраженние , получаем третье уравнение:

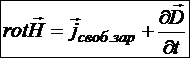
Оно указывает на то, что источником магнитного поля являются не только токи свободных зарядов, но и переменные электрические поля. Это предположение во времена Максвелла не было подтверждено никакими экспериментальными фактами и являлось его гипотезой. Но оно делало магнитное и электрическое поля полностью равноправными в отношении друг друга:

не только переменное магнитное поле порождает электрическое, но и переменное электрическое порождает магнитное.

§23.8. Заключение

Из уравнений Максвелла следует, что отдельно об электрическом и магнитном полях можно говорить только в статических случаях неизменных полей, порожденных неподвижными зарядами и стационарными токами. Если возникает изменение либо электрического, либо магнитного поля из-за нестационарности источников, как тут же в той же точке появляется переменное магнитное или электрическое поле, не связанное ни с какими источниками кроме изменения «противоположного» поля. То есть

в динамике электрическое и магнитное поля неразрывны, и поэтому в этом случае речь может идти только о едином электромагнитном поле.

Такое замыкание полей в теории произошло благодаря предположению Максвелла о токе смещения как источнике магнитного поля.

Прямым следствием системы уравнений Максвелла явилось предсказание существования электромагнитных волн, и именно их открытие стало экспериментальным подтверждением теории Максвелла.