Телесный угол

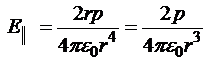
Из последнего рисунка легко увидеть направление искомой напряжённости. Следовательно, на больших расстояниях от центра диполя:

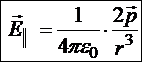
15.4.2. Поле на оси, проходящей через середину плеча диполя перпендикулярно ему

Рис.12.13

Принцип суперпозиции:

Из рисунка 12.13 видно, что

,

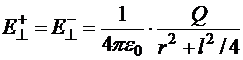кроме этого,

.

При r>>l

.

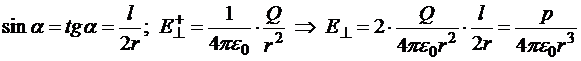Из рисунка видно, что направление искомой напряжённости противоположно дипольному моменту, следовательно, на больших расстояниях от центра диполя:

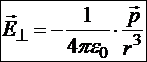
15.4.3. Общий случай на больших расстояниях от центра диполя

Рис.12.14

Разложим дипольный момент на составляющие вдоль вектора (радиальная) и перпендикулярно вектору (нормальная):

.

В соответствие с принципом суперпозиции каждая составляющая дипольного момента порождает свою составляющую полной напряжённости:

.

В соответствие с пунктами 15.4.1 и 15.4.2:

;

;

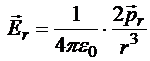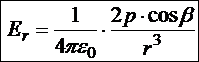
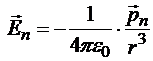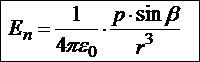
Контрольные вопросы к главе 12

1. Проводящий шар имел электрический заряд 16 Кл, два других таких же шара были не заряжены. Вторым, незаряженным, шаром коснулись сначала заряженного шара, затем третьего незаряженного шара. Затем операцию повторили, коснувшись вновь вторым шаром первого, а затем третьего шара. Какой заряд после этих двух операций получил третий шар. (Ответ: 5 Кл) (§ 12.1)

2. Внутри гладкой непроводящей сферы диаметра 1 м находится маленький шарик массы 10 г, несущий заряд, равный 1 нКл. Какой заряд нужно поместить в нижней точке сферы для того, чтобы шарик удерживался в её верхней точке? (Ответ: Q³2,18×10-2 Кл) (§ 12.1)

3. Тонкая бесконечная нить согнута под углом 90°. Нить несёт заряд, равномерно распределённый с линейной плотностью t=1 мкКл/м. Чему равна сила, действующая на точечный заряд Q=0,1 мкКл, расположенный на продолжении одной из сторон и удалённый от вершины угла на расстояние а=50 см? (Ответ: »4×10-3Н) (§ 12.1)

4. Полусфера несёт заряд равномерно распределённый с поверхностной плотностью s=1 нКл/м2. В центре полусферы находиться точечный заряд Q=0,1 мкКл. С какой силой он воздействует на полусферу? (Ответ: »3 мкН) (§ 12.1)

5 Расстояние между двумя точечными зарядами q и -5q равно 10 см. На каком расстоянии от большего по модулю заряда находится точка, в которой электрическая напряжённость равна 0? (Ответ: »18 см) (§ 12.3)

6. Тонкое полукольцо радиусом 10 см несёт равномерно распределённый заряд с линейной плотностью 1 мкКл/м. Чему равна напряжённость электрического поля в центре полукольца? (Ответ: »1,8×10-5 В/м) (§ 12.3)

7. На рисунке изображена взаимная ориентация двух одинаковых электрических диполей, модуль дипольных моментов которых равен 5×10-9 Кл×м. Расстояние между диполями значительно больше их плеч и равно 1 см. Чему равны механические моменты М12 и М21, воздействующие на второй диполь со стороны поля первого и на первый диполь со стороны поля второго? (Ответ: 450 мН×м; 225 мН×м) (§ 12.4)

Глава 13. ЭЛЕКТРОСТАТИКА. ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА ДЛЯ НАПРЯЖЁННОСТИ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ В ВАКУУМЕ

§13.1. Вектор площади

В механике обсуждалась векторная природа площади, и вводился вектор площади плоской поверхности

,

где − орт нормали к поверхности.

Рис.13.1

В случае, если поверхность не плоская, речь всегда идёт о векторе элементарной поверхности

.

Тогда орт − нормаль к касательной плоскости в точке нахождения элементарной поверхности.

Понятно, что нормаль к плоскости можно провести в двух противоположных направлениях. Выбор правильного направления может быть связан с разными критериями. В механике использовался критерий направления обхода площади по периметру. В данной теме мы будем иметь дело только с замкнутыми поверхностями. Правильный выбор орта нормали такой, чтобы он был обращён вовне замкнутой поверхности:

Рис.13.2

С векторами площадей можно производить все векторные операции, в том числе их можно скалярно умножать друг на друга и проецировать на определённое направление. Рассмотрим большую поверхность, направление которой определяется нормалью , и поверхность поменьше, вектор которой обозначим . По правилам векторной алгебры проекция вектора на направление равно скалярному произведению

.

Рис.13.3

Геометрический смысл этой операции показан на рисунке 13.3. Площадь S1 является участком исходной большой поверхности, каждая точка которого представляет собой пересечение этой поверхности с перпендикуляром, опущенным на неё из соответствующей точки S2.

§13.2. Телесный угол

Рассмотрим элементарную поверхность dSсф, принадлежащую сфере с центром в точке О радиуса r. По определению телесным углом dW, под которым видна часть поверхности сферы dSсф из центра сферы, называется отношение площади dSсф к квадрату радиуса сферы:

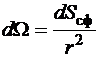
Рис.13.4

Это безразмерная величина, которая является характеристикой совокупности направлений, выходящих из точки О и пересекающих элемент поверхности dSсф и его периметр.

dW численно равен элементу поверхности сферы единичного радиуса, пересекаемого теми же направлениями. Полный телесный угол W равен полной поверхности сферы единичного радиуса, то есть 4p.