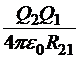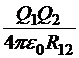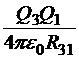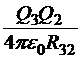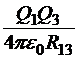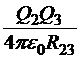ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнПрямая бесконечная однородно заряженная нить
,
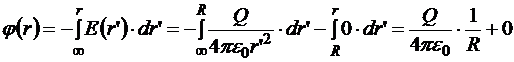следовательно, потенциал внутри сферы будет совпадать с потенциалом поверхности, то есть в данном случае это будет эквипотенциальный объём. Теперь сформулируем вывод:
на поверхности и за пределами равномерно заряженной сферы потенциал электростатического поля ничем не отличается от потенциала поля точечного заряда, помещённого в центр сферы и равного заряду сферы; внутри сферы потенциал постоянный и равен потенциалу на поверхности.
Рис.14.7
14.5.3. Однородное поле
Рис.14.8
Начало отсчёта потенциала берём на месте плоскости заряда (рис.14.8). Поскольку распределение заряда безгранично, выбор начала отсчёта потенциала на бесконечности приведёт к расходимости в интеграле. Поэтому так делать в этом случае нельзя.
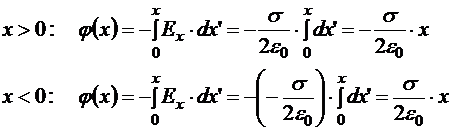
Рис.14.9
15.5.4. Прямая бесконечная однородно заряженная нить
Это тоже неограниченное в пространстве распределение заряда. На бесконечном удалении брать нельзя, но и на самой нити − тоже, так как в этом случае тоже получится расходимость. Начало отсчёта берём на расстоянии от нити, равном 1м. Обозначим расстояние от нити r.
;
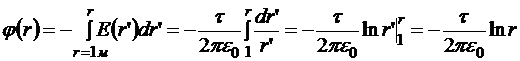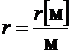− безразмерное.
Рис.14.10
§14.6. Энергия системы точечных зарядов
До сих пор мы рассматривали потенциальную энергию пробного заряда в поле источников. Теперь мы ставим вопрос об энергии, которой обладает система источников сама по себе. Есть эта энергия или её нет? Ответ на этот вопрос является одновременно ответом на вопрос: а нужно ли было совершить работу для создания этой системы, поскольку из закона изменения механической энергии в отсутствии внешних потенциальных полей следует
.
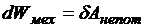В нашем случае работу непотенциальных сил должны выполнять внешние по отношению к системе силы. Кроме этого, мы будем рассматривать только неподвижные заряды, и до воздействия внешних сил, и тогда, когда заряды уже собраны в систему. Поэтому изменение механической энергии будет совпадать с изменением потенциальной энергии взаимного расположения источников. Тогда закон изменения механической энергии примет вид:
В интегральной форме:
Очевидно, что конфигурация бесконечного удаления источников друг от друга может считаться началом отсчёта потенциальной энергии. Поэтому из последнего соотношения получим способ для определения потенциальной энергии взаимного расположения источников или энергии системы точечных зарядов:
.
Здесь под Авнеш нужно понимать работу внешних сил по сведению точечных источников в данную конфигурацию из конфигурации их бесконечного удаления друг от друга.
Рассмотрим систему двух точечных источников Q1 и Q2, отстоящих друг от друга на расстояние R12. Работа внешних сил по сближению их из бесконечного удаления до указанного расстояния не должна зависеть от способа сближения. Поэтому мы в праве выбрать тот способ сближения, который наиболее удобен с точки зрения вычислений. Это способ, когда один заряд неподвижен и может играть роль источника, а второй перемещается по направлению к первому и играет роль пробного заряда. Тогда потенциальная энергия конфигурации — это потенциальная энергия пробного заряда в поле источника, то есть
Хотя, для получения этого результата мы отдали роль источника заряду Q1, а пробного − заряду Q2, выражение показывает, что оба заряда, на самом деле равноправны.
Можно нарисовать матрицу 2´2, номера столбцов которой будут, например, номерами возможных источников, а номера строк − номерами возможных пробных зарядов:
|
1 |
2 |
|
|
1 |
|
|
|
2 |
|
Для краткости обозначим: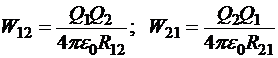 
.Тогда можно записать, что 
, или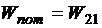 
, но можно и так:
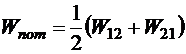
Установив в нужном месте заряды Q1 и Q2, будем приближать к ним заряд Q3, создавая систему из трёх зарядов. Очевидно, что к уже сделанной работе мы добавим слагаемые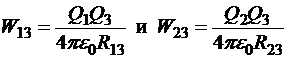 
, которые получаются, если заряд Q3 играет роль пробного в поле источников Q1 и Q2. Но в результате мы можем записать матрицу, в которой уже три заряда могут получить роли как пробных, так и источников:
|
1 |
2 |
3 |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
Теперь энергию системы можно записать как
.
А можно как
Иными словами, для получения системы мы можем суммировать все поддиагональные ячейки, можем суммировать все наддиагональные ячейки. Результат не изменится, так как матрица транспонированная. А можем суммировать все недиагональные ячейки и делить результат пополам. В последнем способе слагаемые можно расставлять множеством способов. Можно так:
,
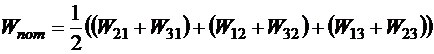то есть суммы каждой строки мы суммировали по всем строкам.
Рассмотрим физический смысл суммы по одной строке, например, по первой:
.
Это произведение первого заряда на потенциал, созданный на его месте всеми зарядами кроме него. Тогда способ суммирования сумм каждой строки по всем строкам можно записать так:
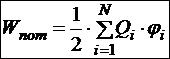
Потенциальная энергия системы зарядов равна полусумме произведений каждого заряда на потенциал, создаваемый на его месте всеми остальными зарядами, кроме него.
Такое представление энергии системы зарядов полезно тем, что позволяет сделать обобщение на случай непрерывного распределения заряда: очевидно, что дискретное суммирование будет заменено интегрированием. Кроме этого, точечный заряд 
является элементарным, то есть пренебрежимо малым по сравнению с полным зарядом системы (в выражении элементарного заряда dV − объём, занимаемый этим зарядом, в котором и создаётся потенциал ). Значит, в выражении
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Написать дипломную работу