Деформация кручения

4.2. Деформация кручения.

Вывод момента для кручения цилиндра:

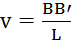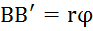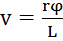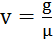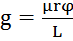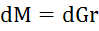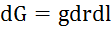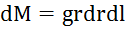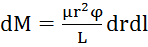(угол поворота стержня), (угол поворота сечения): . Применим формулы для деформации сдвига: , значит . M – крутиильный момент: , где G – сила: , следовательно, или , интегрируем: 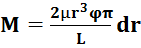. Запишем как: 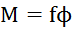–связь момент с углом, где 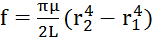крутильная жесткость толостостенной трубки; 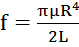– крутильная жесткость сплошного цилиндра. Кручение – неоднородная деформация (внутренние слои испытывают меньшую деформацию, чем внешние).

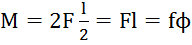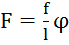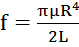Крутильные весы , сила для поворота на угол ϕ , где . Крутильный маятник: момент инерции шариков на концах: 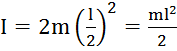. Повернём на угло ϕ0. Угловое ускорение 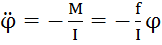. Уравнение гармонических колебаний ϕ= ϕ0cos(ωt+α), где 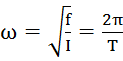или в Герцах: .

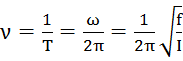4.3. Деформация изгиба.

Изгиб балк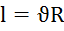и: и 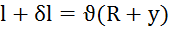, следовательно, 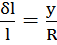; По закону Гука: 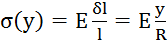. Момент действующий сбоку. 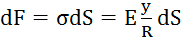, , 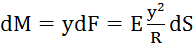, 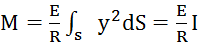где I – момент инерции поперечного сечения балки, относительно поперечной оси, лежащей в нейтральном сечениии 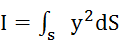. Для круглого сечения радиуса R: dS=rdrdα, y=rsinα: 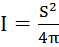. Для прямоугольника со сторонами 2a и 2b: dS=dxdy, S=4ab: .

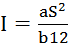Прогиб консольной балки

Момент силы: 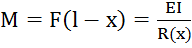, , 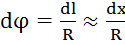значит 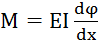, причём 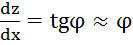, следовательно, 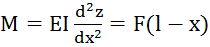, а значит 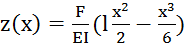. 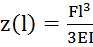– стрела прогиба консольной балки.

Колебания нагруженной балки 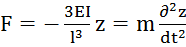. Значит z= z0cos(ωt+α), где

.

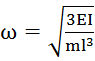Перерезывающая сила. Рассмотри элемент балки dx. Уравнение моментов: M(x)-M(x+dx)-Fndx=0, продефференцируем: 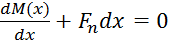, следовательно 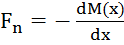(показывает появление сдвиговых деформаций), где 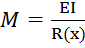, т. е. они появляются при переменном радиусе кривизны R(x).

Устойчивость упругого равновесия: Бифуркация – два (или более) устойчивых положения(F=Fкр). 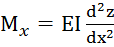; Mx-Fz(x)=0. Решение: z(x)=Acoskx+Bsinkx, где 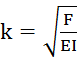. При z(0)=0, kl=πn: 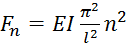, при n=1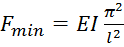

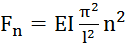при n=1 критическая сила (стержень прямолинейный)

ВОЛНОВЫЕ ЯВЛЕНИЯ В УПРУГИХ СРЕДАХ

Вывод волнового уравнения

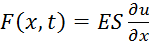из закона Гук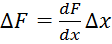а; сила;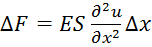; 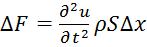2й закон Н;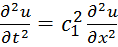

Решение этого уравнения может быть записано в виде суммы двух членов:

u(x, t) = f(x−t) + g(x+t)

Звуковые волны в тонком стержне:

Характеристики звуковой волны, распространяющейся в бесконечном упругом стержне:

u(x, t)=B cos (kx-t+)

такие волны называются гармоническими. Аргумент гармонической функции ϕ =kx − ωt + ϕ0называется фазой волны

Волны в тонких пластинах:

,

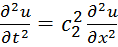Волны в неограниченных упругих средах

Продольные волны — волны, связанные с деформациями растяжения-сдвига внеограниченных упругих средах, причем направление этих деформаций

совпадает с направлением распространения волны.

Закон Гука для продольных деформаций:

.
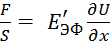