Диаграмма растяжения

Диаграмма растяжения

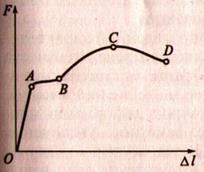
1. Образец из низкоуглеродистой стали – диаграмма для образца

2. Диаграмма – в координатах F, l∆

3. Четыре зоны на диаграмме:

А) зона упругости – материал работает по закону Гука (для наглядности – отступление от масштаба) – удлинения малы и ОА почти совпадала бы с осью F

Б) зона общей текучести (площадка текучести) – существенное изменение длины образца без заметного увеличения нагрузки (не у всех металлов – у Al, легированных сталей нет)

В) зона упрочнения – удлинение сопровождается возрастанием нагрузки.

— Здесь намечается место будущего разрыва шейка – местное сужение образца.

Г) зона местной текучести

— от точки С сила уменьшается, но образец удлиняется

— шейка прогрессирует

— удлинение носит местный характер

Д) точка Д — разрушение образца

Относительная поперечная деформация. Коэффициент Пуассона.

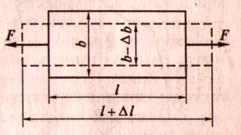
1. Рассматриваем растяжение (сжатие) прямого бруса

2. Брус испытывает как продольные, так и поперечные деформации

3. Удлинение — ∆l, уменьшение ширины бруса на ∆b

4. Относительная продольная деформация ε = ∆ l l

5. Относительная поперечная деформация ε1 = ∆ b b

6. Коэффициент Пуассона – отношение относительной поперечной деформации к относительной продольной деформации (характеризует физические свойства материала: для сталей от 0,25 до 0,35 – таблица)

µ = ε1 ε

Основные механические характеристики материалов

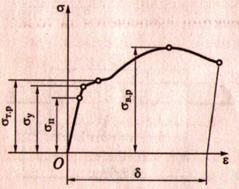
1. Перестроим диаграмму растяжения в координатах – диаграмма для материала:

А) вместо F – σ. Сила F приложена к образцу, напряжение зависит от размера образца σ = NS

Б) вместо ∆l – ε. ∆l – просто удлинение, а ∆l – зависит от длины образца ε = ∆ l l

2. Характерные точки:

А) Предел пропорциональности σп – наибольшее значение напряжения, до которого материал следует закону Гука.

Б) Предел упругости σу – наибольшее значение напряжения, до которого материал не получает остаточных деформаций (восстанавливается)

3. Предел текучести σт. р.– значение напряжения, при котором рост деформации происходит без заметного увеличения нагрузки. (σт. р – текучести на растяжение σт. с – текучести на сжатие, )

Прим. При отсутствии явной площадки текучести принимают напряжение, при котором остаточная деформация 0,2 % — σ0,2 – условный предел текучести)

4. Предел прочности (Временное сопротивление разрыву σв. р., σв. сж – временное сопротивление сжатию).

σв. р., σв. сж являются сравнительными характеристиками прочностных свойств материала и часто используется при расчётах.

Прим. При этом значении материал не разрушается. Фактическое напряжение будет больше, так как площадь поперечного сечения за счёт шейки меньше (σ = NS S меньше – σ будет больше)

5. Относительное удлинение при разрыве (при испытаниях на растяжение) – средняя остаточная деформация к моменту разрыва на определённой стандартной длине образца l0 = 10d, l0 = 5d,

d – диаметр образца.

Расчёты на прочность при растяжении и сжатии

1. Размеры конструкций должны обеспечивать их прочность при наименьших затратах материала.

2. Выявляется точка конструкции с наибольшим напряжением – σнаиб

3. σнаиб должно быть меньше допустимого значения напряжения [σ]

4. Коэффициент запаса n задают при проектировании

А) nТ = 1,5…2 для пластичного материала — от предела текучести

Б) nв = 2,5…4 для хрупкого материала — от предела прочности

В) nв = 2…5 для проектирования строительных сооружений на долгий срок эксплуатации.

5. Допускаемое напряжение

А) для пластичных материалов [σ] = σт. nТ

Б) для хрупких материалов [σ] = σв. nв

6. Условие, из которого определяют размеры проектируемого элемента

σнаиб [σ]

σнаиб = NS [σ]

Самостоятельная работа обучающихся (эзс – 4 час, арх – 6 час, авто – 2)

1. Построить эпюры продольных сил, нормальных напряжений и перемещений для ступенчатого бруса по вариантам

2. Решить задачи на проверку прочности и подбор сечения по вариантам

3. Составить глоссарий основных понятий по теме «Растяжение и сжатие»

1. Расчётно­-графическая работа на построение эпюр продоль­ных сил, напряжений, перемещений сечений бруса, опреде­ление коэффициента запаса прочности — авто

ТЕМА 2.3. ПРАКТИЧЕСКИЕ РАСЧЁТЫ НА СРЕЗ И СМЯТИЕ (4.3. – АВТО)

(эзс – 1 час, арх – 1 час, авто – 1)

Напряжения и деформации при сдвиге (срезе).

1. В поперечном сечении могут возникать как нормальные σ, так и касательные напряжения τ.

2. Рассмотрим короткий брус, жёстко заделанный одним концом в стену.

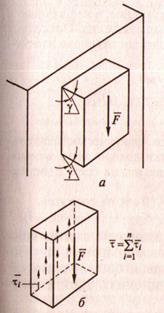
3. Приложим перпендикулярно оси бруса силу в плоскости поперечных сечений возникнет касательное напряжение τ и равнодействующая касательных напряжений Q τ = QS

4. Параллельные сечения бруса сдвигаются относительно друг друга так, что верхняя грань образует угол γ с горизонталью.

Сравнение формул расчёта касательных и нормальных напряжений

Основные допущения для практических расчётов на срез

1. В поперечном сечении возможного среза детали возникает только один силовой фактор — поперечная сила Q

2. Касательные напряжения в поперечном сечении распределены равномерно

3. Если соединение выполнено несколькими одинаковыми деталями (болтами, заклёпками), считают, что все они нагружены одинаково.

Закон Гука при сдвиге.

1. Касательное напряжение τ прямо пропорционально угловой деформации γ

τ = G γ

G – модуль упругости при сдвиге

2. Аналогично закон Гука для растяжения (сжатия)

σ = Е ε

Срез

1. Пример среза:

А) при резке бумаги или стальной полосы

Б) для клёпаного соединения – если приложенная сила больше допустимой

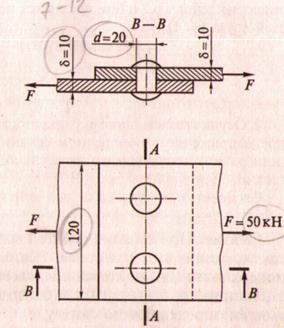
1. Приложенные силы вызывают деформацию сдвига.

2. После снятия нагрузки при сдвиге остаётся намеченное место среза.

3. Срез – может произойти под действием сил, вызывающих деформацию сдвига — при достижении предельных напряжений.