Уравнение движения тягового элемента цепного конвейера

Поскольку сила к цепи прикладывается мгновенно, производя удар, то динамическая нагрузка на цепь составит

Sд. ц= 4mпр·аmax, (9.4)

а расчётная динамическая нагрузка будет:

Sд= 4mпр·аmax- mпр·аmax = 3mпр·аmax, (9.5)

где mпр – приведенная масса для цепного конвейера

mпр = (mг + λmk)·L.

Здесь mг и mk – погонные массы груза и движущихся частей конвейера; L – длина конвейера; λ – коэффициент, учитывающий участие массы обратной ветви в колебательном движении.

Подставив в формулу (9.5) значение аmax, получим выражение для динамического усилия:

Sд = 6(πυ/z0)2·L·mпр/ρ.

Чтобы снизить динамические нагрузки в цепных конвейерах, применяют уравнительные приводы, создающие почти равномерную скорость цепи (рис. 9.2).

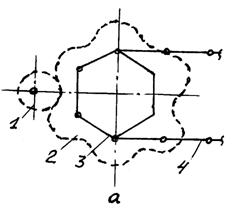
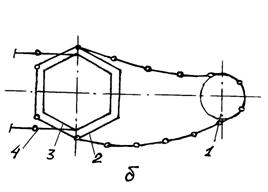
Рисунок 9.2 — Схемы уравнительных приводов

В уравнительном приводе (рис. 10.2, а) с некруглым зубчатым колесом 2 число впадин равно числу зубьев тяговой звездочки 3. Эта звёздочка вращается с переменной скоростью и обеспечивает практически постоянную скорость цепи 4 конвейера.

Уравнительный механизм с короткозвенной цепной передачей 1 (рис 9.2, б) обеспечивает скорость тяговой цепи 4, близкую к равномерной.

Основная литература [5, с. 72…74]

Дополнительная литература [10, с. 342…346]

Контрольные вопросы:

1.  Назовите причину пульсирующего движения цепи в цепных конвейерах.

2.  Напишите выражение для динамического усилия в цепи конвейера.

3.  Какие меры предусматривают в цепных конвейерах для снижения динамических нагрузок?

Лекция 10

Уравнение движения тягового элемента цепного конвейера

Уравнение продольных колебаний цепи можно получить, рассматривая равновесие её элементарного отрезка длиной δх (рис 10.1). При этом отрезок цепи рассматривают как эквивалентный упругий стержень. Краевые условия выбирают в зависимости от того, какой режим работы конвейера рассматривают: пусковой или установившийся.

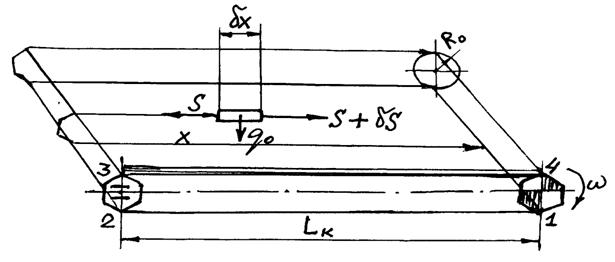
Рисунок 10.1 — Схема для определения динамических параметров конвейера, характеризующих продольные колебания цепи

Растягивающую силу S определяют как произведение относительной деформации ðuц/ðх на жёсткость c0, т. е.

S = c0· ∂uц/∂х, (10.1)

где uц – удлинение цепи; х – длина цепи от точки 1 возбуждения колебаний до рассматриваемого элемента.

Сила, действующая в сечении, смежном с сечением, в котором действует сила S, равна:

S + δS = c0(+δx).

Приращение силы δS = c0δx,

а сила инерции δJи = qц·(j + ∂2uц/∂t2)δx,

где j – ускорение колеблющегося элемента.

Элементарная сила сопротивления движению цепи равна

δW = — gqц·w·δx,

где w – усреднённый коэффициент сопротивления движению.

Уравнение движения элемента: δS — δJи – δW = 0

или c0δx – q0(j + )δx — gqцω·δx = 0,

где q0 – распределённая масса цепи.

После преобразования находим

υ 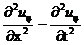= j + gω. (10.2)

Таким образом, получено искомое волновое уравнение вынужденных колебаний эквивалентного цепи стержня, происходящих под действием внешнего периодического возмущения.

Собственные (свободные) колебания цепи описываются уравнением

υ2· ∂2uц/∂х2 – ∂2uц/∂t2 = 0 (10.3)

Появившиеся в цепи упругие волны отражаются в точках контакта её со звёздочками и, двигаясь навстречу вновь возбужденным волнам, интерферируют. Интерференция упругих волн может вызвать высокие динамические усилия в цепи, особенно при резонансе. Последний возникает при совпадении частот вынужденных и собственных колебаний τ1′ и периода τв изменения вынуждающей силы: τ1’= 2Lц/υ; τв= 2π/(ωz0).

Условие возникновения резонанса имеет вид

2π/(ωz0) = 2Lц/υ,

откуда ωz0Lц/(πυ) = 1.

В общем случае это условие выражается так:

vLц/(Ɩ0υ) = А’, (10.4)

где А’=(2i ±1)/(2i) – коэффициент пропорциональности; i – любое целое число; Ɩ0 – шаг цепи; v – средняя скорость цепи; υ – скорость распространения вдоль цепи динамических деформаций:

υ =

Здесь Ец – модуль упругости эквивалентного стержня; ρц – плотность упругого, эквивалентного полотну цепи стержня.

Следует стремиться к тому, чтобы выбранные параметры конвейера v, Ɩ0 и другие определяли значения А’, лежащие в средней части промежутков между его критическими значениями.

Основная литература [5, с.74…79]

Дополнительная литература [10, с.359…360]

Контрольные вопросы:

1.  Как рассматривают отрезок цепи с целью получения уравнения её продольных колебаний?

2.  Напишите волновое уравнение вынужденных продольных колебаний цепи конвейера, возникающих от действия внешнего периодического возмущения.

3.  Как в общем случае выражается условие возникновения резонанса в цепи конвейера?

Лекция 11

Основы динамики землеройно-транспортных машин

11.1 Особенности рабочего процесса землеройно-транспортных машин (ЗТМ)

На земляных работах всё шире применяют высокоэффективные ЗТМ — бульдозеры, скреперы, автогрейдеры, грейдер-элеваторы. Общей принципиальной особенностью этих средств механизации является реализация движущей силы, необходимой для копания, в результате взаимодействия с грунтом ходовых устройств машин.

Нагрузки, действующие на ЗТМ в условиях эксплуатации, разделяют на нормальные, случайные и аварийные.

Нормальными называют нагрузки (усилия), возникающие в условиях обычной эксплуатации машин. Нормальные усилия являются основой для расчёта элементов машин на усталостную прочность.

Если установлено, что вероятность появления неблагоприятной комбинации усилий достаточно велика, то нагрузка относится к категории случайных и по ней ведётся расчёт машины на статическую прочность.

При аварийных нагрузках конструкция ЗТМ приходит в неработоспособное состояние.

Работа современных ЗТМ протекает в условиях переменных нагрузок, в значительном диапазоне скоростей, при переменных скоростях и часто при неустановившихся режимах движения. Колебания скорости, вызванные возрастанием сопротивлений, приводят к возникновению динамических нагрузок на рабочее оборудование и силовые элементы конструкции, приводящие это оборудование ЗТМ в движение.

Рассмотренные особенности рабочих процессов ЗТМ дают основание характеризовать режим их работы как тяжёлый, переменный режим.

11.2 Обоснование расчётной схемы ЗТМ

При составлении расчётных схем для определения динамических нагрузок на элементы ЗТМ необходимо знать жёсткости препятствий и рабочего оборудования. К непреодолимым препятствиям относятся: массив мёрзлого грунта или камни, балки, сваи и т. п.

Жёсткости препятствий, встречающихся при работе ЗТМ, определяются экспериментально с учётом деформации самого препятствия и грунта, в котором оно находится. Жёсткость металлоконструкций навесного рабочего оборудования определяется также экспериментально. Для бульдозера её ориентировочно можно определить по зависимости:

cмк = α·Q,

где Q – масса трактора; α – коэффициент, равный 0,9…1,0.

Жёсткость препятствия cпр и металлоконструкции cмк можно рассматривать как две последовательно соединённые жёсткости, а приведенную жёсткость cп найти из равенства

1/cп = 1/cмк+1/cпр

Приведение масс ЗТМ выполняется по общим правилам механики. В качестве центра приведения выбирается вал двигателя, вал ведущей звёздочки или колеса, а также поступательно движущаяся масса агрегата (рис.11.1).

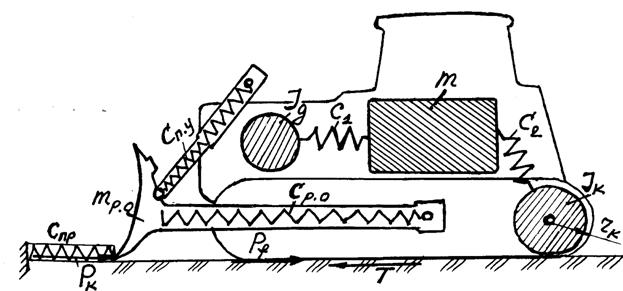
Рисунок 11.1 — Эквивалентная динамическая схема бульдозера

При приведении масс к вращающемуся валу выражение для определения суммарного приведенного момента инерции агрегата будет:

Jв = + m . (11.2)

При приведении масс к поступательно движущейся массе выражение для определения суммарной приведенной массы агрегата имеет вид:

mпр=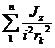+ m. (11.3)