Дифференциальные уравнения равновесия жидкости

В пределе, когда размеры клина будут приближаться к нулю, рср x и рср n будут стремиться к значениям гидростатического давления в точке в направлениях оси Х-Рх и наклонной грани n – Pn, и вследствие этого при переходе к пределу при δх = 0 получаем: рх – рn = 0 или рх = рn.

Составив уравнение проекции сил на оси y и z, найдем, что ру = рп; рz = рn, откуда

Px = Py = Pz = Pn.. (3.2)

Последнее равенствопоказывает, что гидростатическое давление в точке покоящейся жидкости имеет значение, не зависящее от направления площадки, для которой оно вычислено.

Но гидростатическое давление в различных точках не будет одинаковым. Для разных точек давление будет являться непрерывной функцией координат.

3.2. Дифференциальные уравнения равновесия жидкости

(уравнения Леонарда Эйлера)

Целью вывода этих уравнений будет ответ на вопрос: какими по своей природе должны быть силы, под действием которых жидкость будет находиться в равновесии? Для вывода этих уравнений в жидкости, находящейся в покое, условно разместим систему координат и выделим элементарный объем в виде прямоугольного параллелепипеда с ребрами δx, δy, δz (рис.3.9).

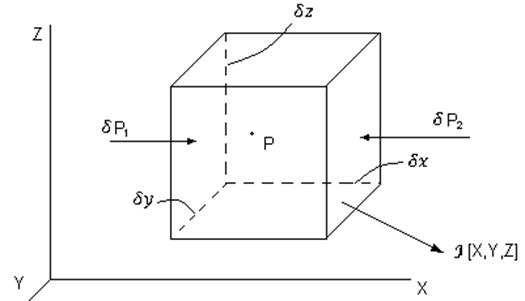
Рис.3.9

Применим принцип отвердевания. В этом случае при рассмотрении тела в покое можно применить законы механики твердого тела, т. е. если тело находится в равновесии, то сумма проекций всех сил на соответствующие оси равна нулю:

ΣРх = 0; ΣРу = 0; ΣРz = 0. (3.3)

На выделенный объем действует массовая сила, вызванная ускорением J, проекции которого на соответствующие оси будут равны X, Y,Z, и поверхностные силы δРi.

Рассмотрим условие равновесия по оси Х. Допустим, на левую грань параллелепипеда действует элементарная сила δР1, на правую δР2:

ΣРх = δР1-δР2+ХδМ=0. (3.4)

Ввиду малости размеров граней параллелепипеда будем считать, что давление на каждую из них будет одинаковым и каким-то средним, тогда

(3.5)

Выразим давления и 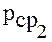через давление р в центре параллелепипеда.

Так как жидкость является сплошной средой (т. е. средой без пустот и переуплотнений), то изменение давления на каком-то элементарном перемещении является непрерывной функции координат:

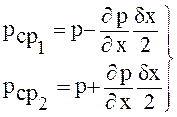, (3.6)

где — градиент гидростатического давления, т. е. частная производная от давления по оси Х.

Подставим выражение (3.6) в (3.5)6

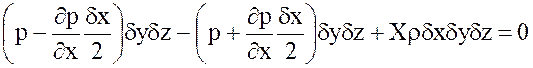
Сократим на δх·δу·δz, т. е. на объем δW, и переходя к пределу:

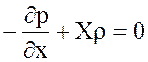. (3.7)

Аналогично рассуждая, но проектируя силы на оси Y и Z, получим еще два уравнения равновесия.

Общепринятая форма записи этих уравнений выглядит так:

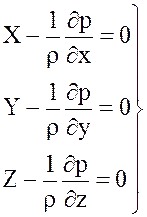(3.8)

Уравнения (3.8) представляют собой общие дифференциальные уравнения равновесия жидкости, из которых следует, что при перемещении в жидкости давление зависит от плотности и ускорения.

Для лучшего понимания смысла полученных уравнений и практического пользования удобнее вместо системы уравнений (3.8) получить одно эквивалентное им уравнение. Для этого левую и правую части уравнений умножим соответственно на dx, dу, dz и сложим

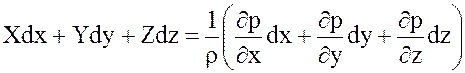, (3.9)

где 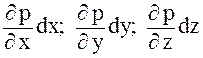— частные дифференциалы давления; они по соответствующим осям определяют изменение (увеличение или уменьшение) давления при переходе на расстояние dx, dy, dz.

Так как гидростатическое давление есть функция только координат, выражение в скобках уравнения (3.9) представляет собой полный дифференциал гидростатического давления:

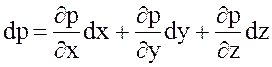. (3.10)

в связи с этим получим одно дифференциальное уравнение для жидкости, находящейся в относительном покое:

. (3.11)

плотность жидкости ρ в уравнении (3.11) можно принять постоянной величиной, поэтому уравнение (3.11) может иметь смысл только в том случае, если его правая часть также является полным дифференциалом. Для этого необходимо, чтобы существовала некая функция U = f(Х, Y,Z), частные производные которой по осям x, y,z были бы равны:

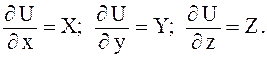
Такая функция называется потенциальной, или силовой, а силы, которые этой функцией выражаются – силами, имеющими потенциал.

Следовательно, жидкость находится в равновесии под действием сил, имеющих потенциал. Из механики известны многие силы, имеющие потенциал. Наибольшее значение из них имеют силы тяжести и силы инерции.

3.3. Основное уравнение гидростатики. Эпюры

гидростатического давления

Это уравнение есть уравнение равновесия жидкости, находящейся под действием только сил тяжести.

В уравнении Эйлера (3.11) проекции ускорений для земных условий равны:

Х, У = 0; Z = — g.

Тогда уравнение (3.11) можно представить в виде

(3.12)

Уравнение (3.12) является дифференциальным уравнением равновесия жидкости, находящейся под действием сил тяжести. Преобразуем его. поскольку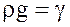, то 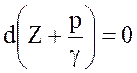, т. е. в любом случае 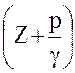всегда остается величиной постоянной, но запишем ее по-иному:

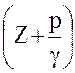= idem; (3.13)

idem – здесь и в дальнейшем употребляется только в смысле «одно и то же», т. е. имеющее одно и то же значение в рассматриваемой области (в объеме или на линии) лишь в данный момент времени, в отличие от const, означающей постоянство величины во времени. В выражении (3.13) Z – геометрический напор; — пьезометрический напор; 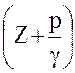— гидростатический напор.

Проиллюстрируем величину 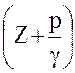рисунком 3.10.

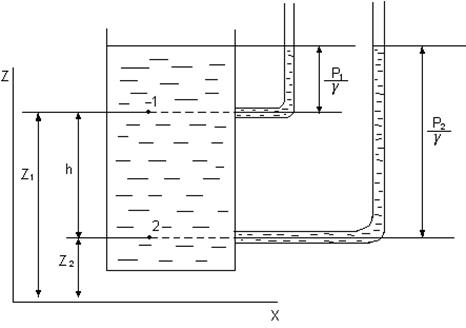
Рис.3.10

Для точек 1 и 2 в сосуде

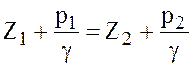; (3.14)

так как Z1 – Z2=h, то

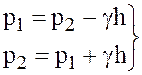(3.15)

Уравнения (3.13), (3.14) или (3.15) называются основным уравнением гидростатики.

Вывод: потенциальная энергия в любой точке покоящейся жидкости является величиной постоянной.

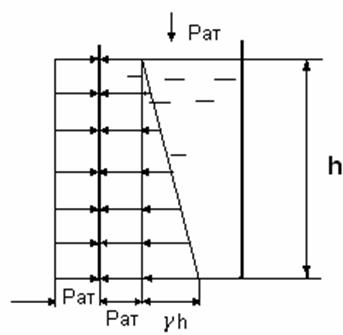
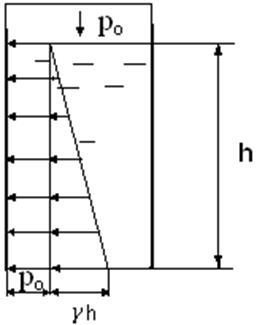
Эпюры гидростатического давления есть графическое выражение закона изменения давления по глубине жидкости.

Рассмотрим несколько типовых случаев.

1. Сосуд с вертикальными плоскими стенками заполнен жидкостью на глубину h и открыт сверху, т. е. на поверхности действует атмосферное давление рат (рис.3.11).