Дифракция фраунгофера на дифракционной решетке
Справа и слева от центрального видны максимумы первого, второго и других порядков, причем ближе к центру дифракционной картины располагается фиолетовый край спектра (т. к. длина волны фиолетового света меньше длины волны красного света и в соответствие с формулой (3-10) угол отклонения фиолетовых линий меньше угла отклонения линий красного цвета для конкретного порядка.
 3.6. Дифракция Фраунгофера на дифракционной решетке
3.6. Дифракция Фраунгофера на дифракционной решетке
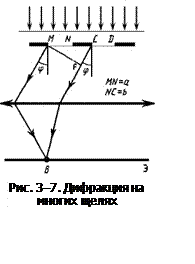
Одномерная дифракционная решетка — система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. На рис. 3-7 для наглядности показаны только две соседние щели MN и CD. Ширина каждой щели а, а ширина непрозрачных участков между щелями b, величина d = a + b называется постоянной дифракционной решетки (периодом). Щели находятся друг от друга на одинаковых расстояниях поэтому разности хода лучей, идущих от соседних щелей, будут для данного направления j одинаковы в пределах всей дифракционной решетки:
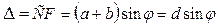 . (3-11)
. (3-11)
В точке В на экране в фокальной плоскости линзы соберутся лучи, которые до линзы были параллельны между собой и распространялись под углом j к направлению падающей волны.
Колебание в точке В является результатом интерференции вторичных волн, проходящих от разных щелей. Для того, чтобы в точке В наблюдался интерференционный максимум, разность хода Δ между волнами, испущенными соседними щелями, должна быть равна целому числу длин волн (четному числу полуволн):
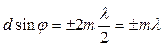 (m=0, 1, 2, …). (3-12)
(m=0, 1, 2, …). (3-12)
При разности хода, равной нечетному числу полуволн, в точке В будет наблюдаться интерференционный минимум:
 (m=0, 1, 2, …). (3-13)
(m=0, 1, 2, …). (3-13)
При пропускании через решетку белого света все максимумы, кроме центрального (m = 0), разложатся в спектр, фиолетовая область которого будет обращена к центру дифракционной картины, красная — наружу. Это следует из формулы (3-12) в которой угол отклонения m – го максимума j ~ l. Это используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов), т. е. дифракционная решетка может быть использована как спектральный прибор. Распределение энергии по спектрам разных порядков показывает, что значительная часть энергии сосредоточена в спектре нулевого порядка (рис. 3-6, б ) и по мере перехода к высшим порядкам энергия быстро убывает. Спектральные приборы, снабженные такими дифракционными решетками, были бы мало светосильны. Устранить данный недостаток предложил английский физик Дж. У. Рэлей, а осуществил это предложение американский физик Р. У.Вуд. Было предложено ввести дополнительную разность хода в пределах каждого штриха решетки. С этой целью решетку гравируют так, что каждая борозда имеет определенный профиль, благодаря чему при отражении (или при прохождении) возникает добавочная разность хода от одного края борозды до другого (рис. 3-8). Подбирая профиль борозды, удается сконцентрировать энергию в спектре того или иного порядка, ослабляя остальные, в том числе и самый яркий спектр нулевого порядка. Решетки подобного типа позволили сделать дифракционные спектрографы инструментом, превосходящим по светосиле обычные
 |
призматические спектрографы.
Решетки, изображенные на рис. 3-8, представляют собой фазовые решетки, отдельные элементы которых отличаются не различием в отражающей или пропускающей способности, влияющей на амплитуду волны, а своей способностью изменять фазу волны. В данном случае изменение фазы происходит вследствие геометрической формы пластинки, отражающей или пропускающей волну.
Можно воздействовать на фазу волны за счет различия в показателе преломления пропускающего слоя при его неизменной толщине; такого рода фазовые решетки удается создавать, вызывая в прозрачном теле ультраакустическую волну.
Фазовая отражательная решетка, использующая различие в изменении фазы при полном внутреннем отражении от серебра и стекла показана на рис. 3-9. Для этого на гипотенузную грань стеклянной 90-градусной поворотной призмы были нанесены полоски серебра, которые разделены полосками стекла без 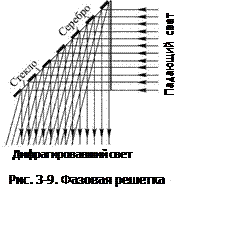 серебрения. При падении света со стороны стекла интенсивность света, отраженного от тех или иных полосок, практически одинакова (за счет полного внутреннего отражения), но возникает различие в фазах, которое и приводит к образованию дифракционной картины. Возможны, конечно, решетки амплитудно-фазовые, т. е. воздействующие одновременно как на фазу, так и на амплитуду.
серебрения. При падении света со стороны стекла интенсивность света, отраженного от тех или иных полосок, практически одинакова (за счет полного внутреннего отражения), но возникает различие в фазах, которое и приводит к образованию дифракционной картины. Возможны, конечно, решетки амплитудно-фазовые, т. е. воздействующие одновременно как на фазу, так и на амплитуду.
3.7. Дифракция на пространственной решетке
Дифракция света наблюдается не только на плоской одномерной решетке (штрихи нанесены перпендикулярно некоторой прямой линии), но и на двумерной решетке (штрихи нанесены во взаимно перпендикулярных направлениях в одной и той же плоскости). Большой интерес представляет также дифракция на пространственных (трехмерных) решетках — пространственных образованиях, в которых элементы структуры подобны по форме, имеют геометрически правильное и периодически повторяющееся расположение, а также постоянные (периоды) решеток, соизмеримые с длиной волны электромагнитного Для наблюдения дифракционной картины необходимо, чтобы постоянная решетки была того же порядка, что и длина волны падающего излучения. Кристаллы, являясь трехмерными пространственными решетками, имеют постоянную порядка 10-10 м и непригодны для наблюдения дифракции в видимом свете (l ~ 5×10-7 м). Немецкий физик М. Лауэ (1879—1960) пришёл к выводу, что в качестве естественных дифракционных решеток для рентгеновского излучения можно использовать кристаллы, поскольку расстояние между атомами в кристаллах одного порядка с длиной волны l рентгеновского излучения (»10-12 ¸10-8 м).
Советский физик Г. В. Вульф и английские физики Г. и Л. Брэгг независимо друг от друга предложили простой метод расчета дифракции рентгеновского излучения от кристаллической решетки. Они предположили, что происходит дифракция рентгеновских лучей при их отражении от системы параллельных кристаллографических плоскостей отстоящих друг от друга на расстоянии d (плоскостей, в которых лежат атомы кристаллической решетки). Монохроматический пучок параллельных рентгеновских лучей (1,2) падает под углом скольжения ![]() (между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1′ и 2′, интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки (рис. 3-10).
(между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1′ и 2′, интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки (рис. 3-10).
Дифракционные максимумы наблюдаются в направлениях, в которых все волны, отраженные атомными плоскостями, будут находиться в одинаковой фазе. Эти направления удовлетворяют формуле Вульфа — Брэггов
![]() (m=1, 2, 3, …), (3-14)
(m=1, 2, 3, …), (3-14)
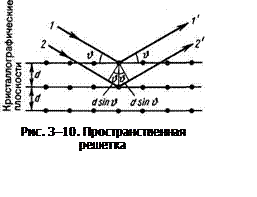 т. е. при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн l, наблюдается дифракционный максимум. Если рентгеновское излучение падает на кристалл под углами скольжения отличными от угла
т. е. при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн l, наблюдается дифракционный максимум. Если рентгеновское излучение падает на кристалл под углами скольжения отличными от угла ![]() , который удовлетворяет соотношению (3-14), то дифракция не возникает.
, который удовлетворяет соотношению (3-14), то дифракция не возникает.
Формула Вульфа — Брэггов используется при решении двух задач:
1. Наблюдая дифракцию рентгеновских лучей известной длины волны на кристаллической структуре неизвестного строения и измеряя ![]() и m, можно найти межплоскостное расстояние (d), т. е. определить структуру вещества (рентгеноструктурный анализ кристаллов).
и m, можно найти межплоскостное расстояние (d), т. е. определить структуру вещества (рентгеноструктурный анализ кристаллов).
2. Наблюдая дифракцию рентгеновских лучей неизвестной длины волны на кристаллической структуре при известном d и измеряя ![]() и m, можно найти длину волны падающего рентгеновского излучения. Этот метод лежит в основе рентгеновской спектроскопии.
и m, можно найти длину волны падающего рентгеновского излучения. Этот метод лежит в основе рентгеновской спектроскопии.
4. Поляризация света
4.1. Естественный и поляризованный свет
Свет, излучаемый отдельным атомом – это электромагнитная волна, т. е. совокупность двух поперечных взаимно перпен-дикулярных волн — электрической (образованной колебанием вектора напряженности электрического поля ![]() ) и магнитной (образованной колебанием вектора напряженности магнитного поля
) и магнитной (образованной колебанием вектора напряженности магнитного поля ![]() ), идущих вдоль общей прямой
), идущих вдоль общей прямой ![]() , называемой световым лучом (рис. 4-1).
, называемой световым лучом (рис. 4-1).


