Для металлов уровень ферми
EF – параметр распределения, называемый энергией или уровнем Ферми (см. дальше).
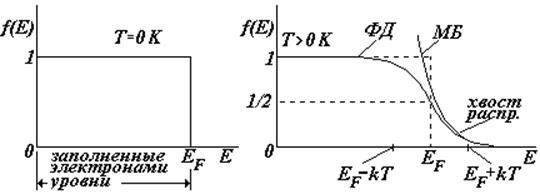
На рисунках показаны графики функции ФД, их часто называют распределением электронов по энергиям. При температуре Т = 0 К вероятность того, что электрон имеет какое-либо значение энергии в пределах 0 ¸ EF равна единице; вероятность обнаружить электрон с энергией > EF равна нулю.
|
|
При температуре
Т > 0 К электроны за счет энергии теплового движения «покидают» свои уровни и переходят на более высокие.
Для металлов уровень Ферми (энергия Ферми) определяется следующим образом. (для полупроводников – см. дальше)
1)При Т = 0 К — это уровень энергии, отделяющий заполненные электронами
уровни от незаполненных или это максимальная энергия
электронов при Т = 0 К
2) При Т > 0 К — это энергетический уровень, который занимает электрон с
вероятностью, равной 1/2.
При высоких температурах или малых концентрациях электронов распределение ФД переходит в классическое распределение МБ. Действительно, при Е-ЕF >> кТ можно пренебречь единицей в знаменателе распределения ФД, тогда получим:
|
|
Иначе говоря, на хвосте распределения (см. рис.) можно использовать классическую формулу.
|
|
Энергия Ферми при Т = 0 К, не зависит от числа электронов в образце и его объема, а определяется только концентрацией электронов n=N / V .Для одновалентных атомов характерны величины EoF @ 100 кТ @ 2,5 эВ |
|
|
Для металлов энергия Ферми очень слабо зависит от температуры (kT / EoF @ 0,01 при комнатных температурах) |
|
|
средняя энергия электронов в зоне проводимости (см. дальше ) связана с энергией Ферми указанным образом |
Зная энергию Ферми EoF можно оценить скорость vF фермиевских электронов и их температуру ТF. Следует иметь в виду, что это не температура вещества, а температура воображаемого облака электронов, средняя скорость движения которых равна vF .
|
Þ vF |
Þ ТF. |
|
элемент |
EoF (эВ) |
ТF., К |
vF, 106 м/с |
|
калий |
2,1 |
25000 |
0,85 |
|
медь |
7,0 |
82000 |
1,6 |
|
золото |
5,5 |
64000 |
1,4 |
ЭЛЕМЕНТЫ ЗОННОЙ ТЕОРИИ ТВЕРДЫХ ТЕЛ.
Зонная теория – это один из разделов квантовой механики твердых тел – теория валентных электронов в периодическом поле кристаллической решетки.
Аналитически решить уравнение Шрёдингера для электрона, движущегося внутри металла, т. е. в поле, создаваемом множеством заряженных ионов решетки, невозможно. Для решения применяют различные приближенные методы.
Образование энергетических зон в кристаллах.
 В отдельном атоме электрон имеет определенный набор энергий Е1, Е2 , Е3 ,…. Это проявляется в том, что спектры одноатомных газов линейчатые, т. е. состоят из отдельных линий. Чистый, без примесей металл состоит из однотипных атомов. При этом от каждого атома отрывается по одному, а у некоторых металлов по два электрона, ионы располагаются в строгом порядке, образуя кристаллическую решетку, а электроны свободно перемещаются внутри решетки, образуя облако электронного газа. Так как атомы однотипны, то у каждого электрона должен быть одинаковый набор энергий. Однако, в соответствии с принципом Паули электроны не могут иметь одинаковые энергии, поэтому в кристалле каждый энергетический уровень расщепляется на множество линий, лежащих вблизи исходного уровня, и образуются энергетические зоны. Не следует понимать эти зоны как некие пространственные области в металле, энергетические зоны это интервалы значений энергий, которые «разрешено» иметь электронам (природой и квантовой механикой). Одни интервалы энергий называются разрешенными зонами, другие – запрещенными, т. е. такие энергии электроны иметь не могут.
В отдельном атоме электрон имеет определенный набор энергий Е1, Е2 , Е3 ,…. Это проявляется в том, что спектры одноатомных газов линейчатые, т. е. состоят из отдельных линий. Чистый, без примесей металл состоит из однотипных атомов. При этом от каждого атома отрывается по одному, а у некоторых металлов по два электрона, ионы располагаются в строгом порядке, образуя кристаллическую решетку, а электроны свободно перемещаются внутри решетки, образуя облако электронного газа. Так как атомы однотипны, то у каждого электрона должен быть одинаковый набор энергий. Однако, в соответствии с принципом Паули электроны не могут иметь одинаковые энергии, поэтому в кристалле каждый энергетический уровень расщепляется на множество линий, лежащих вблизи исходного уровня, и образуются энергетические зоны. Не следует понимать эти зоны как некие пространственные области в металле, энергетические зоны это интервалы значений энергий, которые «разрешено» иметь электронам (природой и квантовой механикой). Одни интервалы энергий называются разрешенными зонами, другие – запрещенными, т. е. такие энергии электроны иметь не могут.
На рисунке показано символически, как можно представить себе образование зон. Здесь r – расстояние между атомами. При сближении атомов до некоторого расстояния r0 образуется кристалл, и, соответственно, энергетические зоны. В некоторых случаях зоны могут перекрываться, образуя более широкую зону. Чем дальше электрон от ядра, тем шире зона. Верхние зоны имеют ширину 1 эВ и более, нижние – несколько сотых эВ.
 Каждый уровень должен расщепляется на N уровней, где N число свободных электронов в системе. Но данную энергию могут иметь 2 электрона с разнонаправленными спинами. Различие в направлениях спинов проявляется только при воздействии внешнего поля. Поэтому иногда говорят, что в зоне 2N уровней, а иногда N уровней, имея в виду, что на каждом уровне по 2 электрона с противоположно направленными спинами (см. рис.). В 1 см 3 Ме примерно 10 22- электронов. Если ширина зоны примерно 1 эВ, следовательно, расстояние между уровнями порядка 10 -22 эВ, поэтому говорят, что уровни в зоне распределены квазинепрерывно.
Каждый уровень должен расщепляется на N уровней, где N число свободных электронов в системе. Но данную энергию могут иметь 2 электрона с разнонаправленными спинами. Различие в направлениях спинов проявляется только при воздействии внешнего поля. Поэтому иногда говорят, что в зоне 2N уровней, а иногда N уровней, имея в виду, что на каждом уровне по 2 электрона с противоположно направленными спинами (см. рис.). В 1 см 3 Ме примерно 10 22- электронов. Если ширина зоны примерно 1 эВ, следовательно, расстояние между уровнями порядка 10 -22 эВ, поэтому говорят, что уровни в зоне распределены квазинепрерывно.
Уровни в зоне распределяются неравномерно, в середине зоны они располагаются гуще. Для характеристики распределения уровней пользуются понятием плотности уровней. Если на интервал энергий dE приходится dZ уровней, то
|
|
плотность энергетических уровней в зоне — по смыслу – это число уровней, приходящихся на единичный интервал энергий. |
|
|
Приближенная формула для зависимости плотности уровней от энергии; С = const для данного объема V тела, m— масса электрона |
Проводники, полупроводники и диэлектрики.
Теоретически количество разрешенных зон бесконечно, а число электронов в данном теле хотя и очень велико, но имеет конечное значение. Поэтому не все зоны заполняются электронами. При температуре Т = 0 К заполнены полностью все зоны с наименьшей энергией, все остальные – пустые. Разрешенные зоны принято изображать прямоугольниками. Т. к. уровней в зоне огромное количество, целесообразно заполненную зону полностью или частично заштриховывать, а незаполненную — оставить пустой. Заполненная зона, граничащая с незаполненной, называется валентной, зона выше валентной называется зоной проводимости
Электрические свойства различных веществ — проводников (металлов), собственных полупроводников, диэлектриков и примесных полупроводников — с позиций зонной теории можно объяснить различной заполненностью зон электронами и шириной запрещенной зоны DЕ. И у металлов и у диэлектриков имеется множество свободных электронов, но у них разные энергетические возможности. Основное, что следует понять, что электрон только тогда «принимает», сообщаемую ему энергию, когда он при этом имеет возможность перейти на более высокий свободный энергетический уровень.

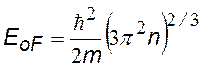



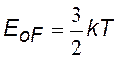
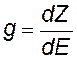 (1/эВ)
(1/эВ)


