Эффект гроба магомета

Теперь мы можем определить диамагнетизм электронной плазмы. Представим, что есть внешнее магнитное поле, направленное вертикально, при этом в любом случае (), внешнее поле будет ослабляться полем магнитного момента одноэлектронного витка с током. Это явление и называется диамагненизмом электронной плазмой.

Следует отметить, что диамагнетизм плазмы связан с орбитальным или токовым движением электрона, а не с собственным магнитным моментом.

б) Прецессия Лармора

Прецессия представляет собой вращение электронных орбиталей атомов, вокруг напряженности магнитного поля.

Рассмотрим одноэлектронный виток с током, находящийся в поле внешних сил, которые обусловлены наличием внешнего магнитного поля. Момент сил, действующий на такой виток:

Связь производной орбитального магнитного момента с магнитным полем можно записать, как:

Воспользовавшись гиромагнитным соотношением для орбитального движения, получим уравнение на механический угловой момент:

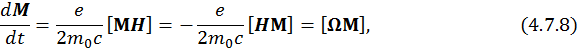
Здесь -частота прецессии Лармора.

в) Эффект « гроба Магомета»

Этот эффект характерен для сверхпроводников, не пропускающих магнитное поле.

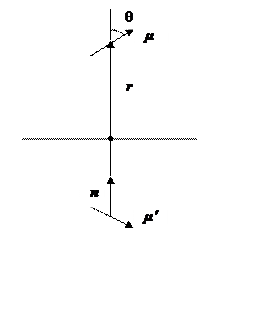
Пусть имеется сверхпроводящая поверхность и магнит. Т. к. силовые линии, исходящие из северного полюса магнита не могут проникнуть в сверхпроводник, то при сближении магнита и сверхпроводящей поверхности происходит отталкивание магнитного момента с его зеркальным изображением в сверхпроводнике.

Ясно, что магнит при сближении со сверхпроводниковой поверхностью будет парить над ней, только если потенциальная энергия имеет минимум:

Для того чтобы найти минимум потенциальной энергии необходимо исследовать эту функцию на экстремум по :

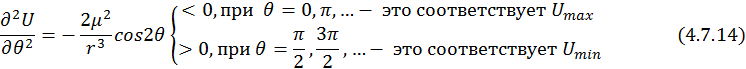
Здесь — угол между вектором нормали и магнитным моментом системы (см. рис.).

Минимум соответствует устойчивому положению системы, когда магнит расположен горизонтально относительно сверхпроводящей плоскости, т. е. при .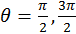

Глава V

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

§ 5.1. Волновое уравнение

В пустом пространстве, т. е. без зарядов и токов электромагнитное поле удовлетворяет уравнению Максвелла:

где 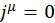, т. к. токи и заряды отсутствуют. Это уравнение движения, вторая пара уравнений Максвелла.

Уравнение (5.1.1) имеет отличное от нуля решение.

Поля, которые существуют сами по себе, называются электромагнитными волнами. Эти поля переменны во времени. Для нахождения уравнения для потенциалов электромагнитного поля подставим в явном виде тензор электромагнитного поля в уравнение (5.1.1).

Это выражение можно упростить, если наложить на потенциалы условие Лоренца: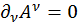
. Тогда уравнение (5.1.2) примет вид:

где □ – оператор Даламбера:

Уравнение 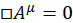– волновое уравнение. Кроме калибровки Лоренца также можно использовать кулоновскую калибровку, которая имеет вид:

В этом случае

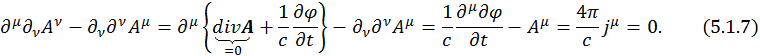
Если расписать все четыре уравнения, то они будут иметь следующий вид:

для векторного потенциала при μ=1,2,3:

для скалярного потенциала при μ=0:

Таким образом, получили

Таким образом, решение уравнения Пуассона:

В случае, точечного заряда решение в виде: 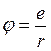— кулоновский потенциал. В этом случае 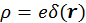. Кулоновский потенциал – статическое поле, а электромагнитные волны переменные во времени. Следовательно, это решение не имеет никакого отношения к электромагнитным волнам. Положим 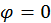. Тогда волновое уравнение в кулоновской калибровке будет иметь вид: