ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнпример расчета сложной цепи переменного тока символическим методом
Расчет сложной цепи переменного тока
символическим методом
Методические указания
к курсовому проектированию
В методических указаниях приведены варианты заданий, пример расчета сложной цепи переменного тока символическим методом и список литературы.
Методические указания предназначены для студентов заочного отделения в соответствии с рабочими программами кафедры электротехники и электроники.
Рис. 2, табл. 2, библиогр. 2 назв.
Расчет сложной цепи переменного тока символическим методом
Задание для расчета:
1. Для цепи переменного тока со смешанным соединением элементов, изображенной на рисунке 1, символическим методом рассчитать следующие величины:
сопротивления и проводимости ветвей параллельного участка 2-3;
суммарную проводимость и сопротивление параллельного участка 2-3;
полное сопротивление цепи;
ток в неразветвленной части цепи;
падение напряжения на параллельном участке схемы;
токи ветвей параллельного участка;
падения напряжения на элементах последовательного участка схемы.
2. Для проверки расчетов сравнить сумму падений напряжения на всех участках цепи с напряжением на входе схемы.
3. Построить векторную диаграмму токов и напряжений.
4. Рассчитать активную, реактивную и полную мощность всей схемы, последовательного участка цепи и ветвей параллельной части схемы.
5. Проверить правильность расчета мощности.
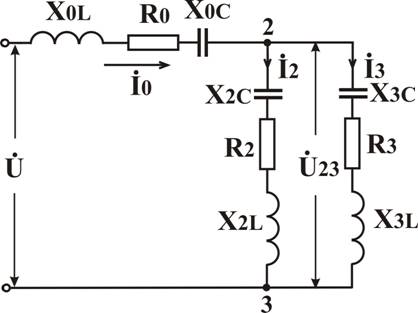
Рисунок 1. Схема цепи переменного тока со
смешанным соединением элементов
Таблица 1. Варианты задания для расчета цепи переменного тока при смешанном соединении элементов.
|
№ вар. |
В |
X0L Ом |
R0 Ом |
X0C Ом |
X2C Ом |
R2 Ом |
X2L Ом |
X3Cb Ом |
R3c Ом |
X3Lc Ом |
|
1 |
|
8 |
3 |
4 |
6 |
8 |
12 |
6 |
3 |
2 |
|
2 |
|
3 |
8 |
9 |
8 |
3 |
4 |
4 |
8 |
10 |
|
3 |
|
8 |
4 |
5 |
3 |
6 |
11 |
6 |
4 |
3 |
|
4 |
|
2 |
6 |
10 |
8 |
4 |
5 |
8 |
6 |
16 |
|
5 |
|
9 |
3 |
5 |
5 |
3 |
9 |
14 |
8 |
8 |
|
6 |
|
4 |
6 |
12 |
12 |
8 |
6 |
8 |
3 |
12 |
|
7 |
|
9 |
8 |
3 |
5 |
6 |
13 |
6 |
4 |
3 |
|
8 |
|
8 |
4 |
11 |
7 |
4 |
4 |
4 |
6 |
12 |
|
9 |
|
11 |
6 |
3 |
12 |
8 |
18 |
12 |
3 |
8 |
|
10 |
|
6 |
3 |
10 |
11 |
6 |
3 |
3 |
4 |
6 |
|
11 |
|
8 |
4 |
5 |
6 |
3 |
10 |
16 |
8 |
10 |
|
12 |
|
7 |
8 |
13 |
8 |
4 |
5 |
10 |
6 |
18 |
|
13 |
|
8 |
3 |
4 |
5 |
6 |
13 |
5 |
4 |
2 |
|
14 |
|
5 |
4 |
8 |
10 |
3 |
6 |
9 |
6 |
17 |
|
15 |
|
16 |
8 |
10 |
8 |
8 |
14 |
8 |
3 |
4 |
|
16 |
|
8 |
6 |
16 |
18 |
6 |
10 |
9 |
4 |
12 |
|
17 |
|
6 |
4 |
3 |
5 |
4 |
8 |
15 |
6 |
7 |
|
18 |
|
2 |
6 |
10 |
15 |
8 |
9 |
3 |
3 |
7 |
|
19 |
|
9 |
3 |
5 |
8 |
3 |
12 |
9 |
8 |
3 |
|
20 |
|
4 |
8 |
10 |
7 |
4 |
4 |
3 |
6 |
11 |
|
21 |
|
9 |
4 |
6 |
10 |
8 |
16 |
10 |
3 |
6 |
|
22 |
|
4 |
3 |
8 |
14 |
6 |
6 |
7 |
4 |
10 |
|
23 |
|
10 |
6 |
2 |
4 |
3 |
8 |
10 |
8 |
4 |
|
24 |
|
5 |
8 |
11 |
12 |
6 |
4 |
10 |
4 |
13 |
|
25 |
|
13 |
4 |
10 |
3 |
8 |
9 |
12 |
3 |
8 |
|
26 |
|
6 |
6 |
14 |
8 |
4 |
5 |
8 |
6 |
16 |
|
27 |
|
14 |
8 |
8 |
6 |
3 |
10 |
12 |
8 |
6 |
|
28 |
|
11 |
3 |
15 |
11 |
8 |
5 |
7 |
3 |
11 |
|
29 |
|
12 |
4 |
9 |
4 |
4 |
7 |
15 |
6 |
7 |
|
30 |
|
6 |
6 |
14 |
13 |
6 |
5 |
9 |
4 |
12 |
Пример расчета:
Таблица 2. Начальные данные для расчета
|
№ вар. |
В |
X0L Ом |
R0 Ом |
X0C Ом |
X2C Ом |
R2 Ом |
X2L Ом |
X3Cb Ом |
R3c Ом |
X3Lc Ом |
|
0 |
|
7 |
4 |
3 |
9 |
8 |
3 |
2 |
3 |
6 |
1. Находим сопротивления и проводимости ветвей параллельного участка 2-3
Сопротивление второй ветви
= 
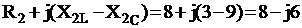Ом
Преобразуем 
в показательную форму 
= 
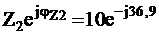Ом
( Z2 =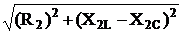 
; φZ2 = 
)
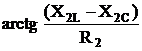Проводимость второй ветви 
= 
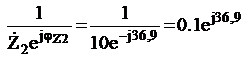См
Преобразуем в алгебраическую форму
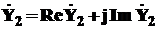
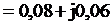См
( 
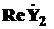= Y2·cosφ ; 
= Y2·sinφ )
Аналогично находим сопротивление и проводимость третьей ветви
= 
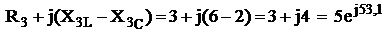Ом
= 
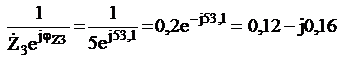См
2. Находим суммарную проводимость и сопротивление параллельного участка схемы 2-3
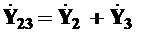= 0,08 +j0,06 + 0,12 – j0,16 = 0,2 – j0,1 См
Преобразуем 
в показательную форму
= 
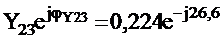См
Сопротивление параллельного участка
= 
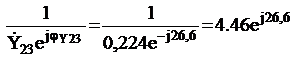Ом
Преобразуем 
в алгебраическую форму 
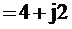Ом
3. Находим полное сопротивление цепи 
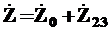
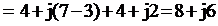Ом
Преобразуем 
в показательную форму 
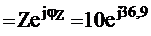Ом
4. Находим ток в неразветвленной части цепи 
Направим приложенное напряжение по вещественной оси 
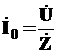
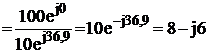А
5. Находим падение напряжения на параллельном участке 2-3
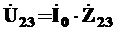
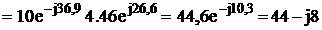В
6. Находим токи ветвей
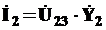
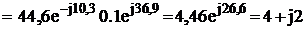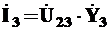
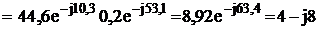А
А
7. Находим падение напряжения на элементах последовательного участка цепи
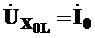
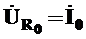
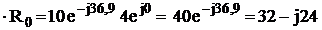В
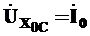
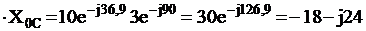В
В
8. Для проверки расчетов найдем векторную сумму падений напряжения на всех участках схемы, она должна быть равна напряжению на входе схемы 100 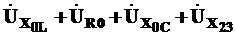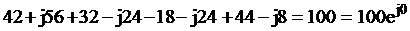В
=
= 
В
9. Построение векторной диаграммы
Диаграмма напряжений — на комплексной плоскости складываем напряжения на всех элементах схемы — строим вектор напряжения на первом элементе последовательного участка цепи 
(по вещественной оси откладываем 
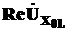, а по мнимой — 
). Из конца этого вектора аналогично строим напряжение на втором элементе последовательного участка цепи 
. – получаем векторную сумму двух напряжений. Аналогично добавляем напряжение 
и 
— получаем векторную сумму напряжений на всех участках цепи, т. е. напряжение на входе схемы.
Диаграмма токов — на комплексной плоскости строим ток второй ветви (по вещественной оси откладываем 
, а по мнимой — 
). Из конца этого вектора аналогично строим ток третьей ветви – получаем векторную сумму токов в ветвях параллельного участка схемы, который должен быть равен рассчитанному значению тока в неразветвленной части цепи 
.
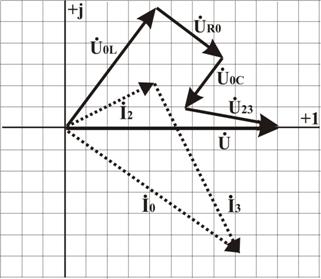
Рисунок 2. Векторная диаграмма цепи переменного тока со
смешанным соединением элементов
10. Расчет мощности всей схемы, последовательного и ветвей параллельного участков цепи.
Полная мощность всей схемы
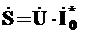
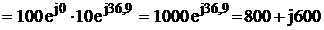ВА
Активная мощность всей схемы P = 
= 800 Вт
Реактивная мощность всей схемы Q = 
= 600 Вар
Полная мощность второй ветви
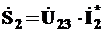
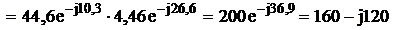ВА
Активная мощность второй ветви P2 = 
= 160 Вт
Реактивная мощность второй ветви Q2 =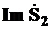 
= – 120 ВАр
Полная мощность третьей ветви
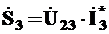
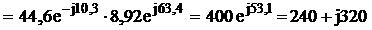ВА
Активная мощность третьей ветви P3 =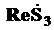
= 240 Вт
Реактивная мощность третьей ветви Q3 =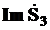 
= 320 ВАр
Полная мощность последовательного участка цепи
= 
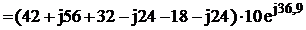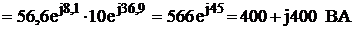
Активная мощность последовательного участка цепи
P0 = 
= 400 Вт
Реактивная мощность последовательного участка цепи
Q0 =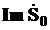 
= 400 ВАр
11. Проверка расчета мощности:
Активная мощность всей схемы (800 Вт) должна быть равна сумме активной мощности последовательной и параллельных ветвей
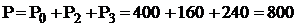Вт
Реактивная мощность всей схемы (600 Вар) должна быть равна алгебраической сумме реактивной мощности последовательной и параллельных ветвей
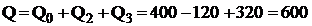Вт
Совпадение полученных результатов свидетельствует о правильности расчета мощности.
Справочные материалы:
Формулы для преобразования комплексных чисел
Алгебраическая форма комплексного числа A = ReA + j ImA = A’ + j A”
Показательная форма комплексного числа A =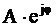 
ReA = A’ = A·cosφ
ImA = A” = A·sinφ
A =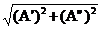 
φ =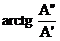 
, если A’ ≥ 0
φ = 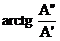+ 180O, если A’ < 0
Литература
Основная
1. Александрова Н. А. Электротехника и электроника [Электронный ресурс] : Учебное пособие / Н. А.Александрова, В. П.Катушкин, В, В.Романенко/ СПбГТИ(ТУ), Электронная библиотека.- СПб.: СПбГТИ(ТУ), 2008.- 98 с.
Дополнительная
2. Иванов, И. И. Электротехника : учебник для неэлектротехнических направлений и специальностей вузов / И. И. Иванов, Г. И. Соловьев, В. С. Равдоник. – Спб. : Лань, 2006 . -496 с.
Содержание
1 Задание для расчета.………………………………………………………. 3
2 Варианты задания для расчета цепи переменного тока при
смешанном соединении элементов………………………………………. 4
3 Пример расчета.……………………………………………………………. 5
4 Литература…………………………………………………………………. 9
Кафедра электротехники и электроники
Методические указания
к курсовому проектированию
Расчет сложной цепи переменного тока
символическим методом
Наталия Александровна Александрова
Виталий Владимирович Романенко
Отпечатано с оригинал–макета. Формат 60х90 1/16
Печ. л. 6.4 Тираж экз.
Санкт-Петербургский государственный технологический институт
(Технический университет)
198013 Санкт-Петербург, Московский пр., д. 26
Типография издательства СПбГТИ (ТУ) т. 49-49-365
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Дипломные работы