методичка к лабораторным по электромеханике

Методические указания к лабораторным работам по дисциплине "Электротехника и электромеханика" для иностранных студентов дневной формы обучения направления 6.050202 «Автоматизация
и компьютерно–интегрированные технологии» / Состав.:
Ю. М. Александров, С. И. Теслюк — Харьков: ХНУРЭ, 2015. – 76 с.

СОДЕРЖАНИЕ

ОБЩИЕ ПОЛОЖЕНИЯ

Электротехника – это наука о методах и технических средствах производства, передачи и применения электрической энергии. Основой дисциплины "Электротехника и электромеханика" является теоретическая электротехника.

Практическое закрепление знаний из основ электротехники и электромеханики проводится на лабораторных занятиях, которые включают как экспериментальные исследования, так и теоретические расчеты по теме эксперимента.

Суть и задачи дисциплины. Дисциплина "Электротехника и электромеханика" принадлежит к циклу общеобразовательных дисциплин, которые оказывают содействие формированию общеинженерного мышления специалиста.

Целью ее изучения является обретение навыков анализа электрических и электромагнитных цепей, расчета их электрических параметров в установленном и переходном режимах.

Изучение дисциплины "Электротехника и электромеханика" обеспечивается знаниями:

– физики;

– математики;

– основ программирования.

Выполнение лабораторных работ по данной дисциплине позволяет студентам проводить натурные эксперименты для закрепления знаний полученных на лекционных, практических и самостоятельных занятиях.

Порядок выполнения лабораторных работ. Лабораторные работы выполняются соответственно расписанию занятий или графика отработок пропущенных работ. Студенты должны приходить на лабораторные работы без опозданий, иначе к выполнению работы не допускаются.

В начале первого занятия все студенты должны ознакомиться с правилами техники безопасности и расписаться в журнале учета выполнения лабораторных работ. Студенты, которые не ознакомились с правилами техники безопасности, к выполнению работ не допускаются.

Во время выполнения лабораторных работ студенты должны постоянно находиться рядом с лабораторным стендом. Запрещается оставлять включенный лабораторный стенд без надзора, выходить из лаборатории можно лишь с разрешения преподавателя.

При выполнении каждой лабораторной работы студенты должны выучить соответствующий раздел лекционного материала, ознакомиться с техническим оборудованием и приборами, которые используются в данной лабораторной работе, режимами их безопасного функционирования.

Перед выполнением работы студенты должны ознакомиться с порядком ее выполнения.

Лабораторные работы выполняются бригадами студентов из 3 человек.

Для осуществления расчетов в лабораторной работе студенты должны иметь инженерные калькуляторы.

Во время выполнения работы студенты несут ответственность за сохранение лабораторного оборудования и порядок на своем рабочем месте.

При нарушении правил проведения лабораторных работ или правил техники безопасности студенты могут быть отстранены от работы.

Во время выполнения лабораторной работы студенты на персональных компьютерах в прикладном пакете Multіsіm Educatіon Edіtіon 10.1.197 собирают соответствующую электрическую цепь. Результаты каждого этапа работы должны предоставляться преподавателю для проверки.

Во время выполнения лабораторной работы каждый студент (в бригаде) должен иметь черновик с записями проведенных измерений, которые должны сохраняться им к защите результатов работы. Во время осуществления расчетов должны записываться все промежуточные преобразования и вычисления с учетом порядка и размерности электрических величин.

Завершающим этапом выполнения лабораторной работы является составления индивидуального отчета. Он должны выполняться соответственно требованиям ДСТУ 3008-95 "Документация. Отчеты в области науки и техники". Для каждой лабораторной работы выполняется отдельный отчет, который после ее защиты остается у преподавателя.

Структура отчета. Отчет должен содержать:

– титульный лист, где указанное название лабораторной работы;

– цель выполняемой работы;

– исходные данные согласно варианту;

– перечень и описание используемого лабораторного оборудования;

– принципиальные схемы исследуемых электрических цепей (приложение В);

– результаты измерений (таблицы, графики, диаграммы);

– результаты расчетов (в том числе с использованием программных средств);

– индивидуальные выводы по результатам выполнения работы.

К началу следующей лабораторной работы студент должен подать преподавателю полностью оформленный отчет о предыдущей работе и защитить ее.

Организация работы.

Лабораторные работы выполняются в прикладном пакете Multіsіm Educatіon Edіtіon 10.1.197, который дает возможность моделирования работы электрических цепей.

1 ИССЛЕДОВАНИЕ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПОСТОЯННОГО ТОКА

1.1 Цель работы

Целью работы является теоретическое и экспериментальное исследования электрической цепи, проверка методов расчета разветвленной электрической цепи, сравнение результатов теоретического и экспериментального исследования, получение практических навыков работы с электрическими цепями и устройствами.

1.2 Методические указания по организации самостоятельной работы студентов

Во время подготовки к лабораторной работе необходимо ознакомиться с работой прикладного пакета Multіsіm Educatіon Edіtіon 10.1.197, обработать теоретический материал из раздела "Линейные электрические цепи постоянного тока", ознакомиться с содержанием лабораторной работы и подготовить бланк отчета.

В работе исследуется линейная электрическая цепь (рис. 1.1), которая содержит шесть резисторов R1 – R6 и два идеальных источника ЭДС (электродвижущей силы) Е1, Е2, внутреннее сопротивление которых равняется нулю. Проводится теоретическое и экспериментальное исследования электрической цепи с помощью прикладного пакета Multіsіm Educatіon Edіtіon 10.1.197 с использованием методов контурных токов, узловых потенциалов, наложения и эквивалентного генератора.

При теоретическом исследовании цепи составляют и решают системы уравнений, которые позволяют аналитически определить контурные токи и узловые напряжения для данной цепи.

Система уравнений по методу контурных токов для n контуров имеет такую каноническую форму записи:

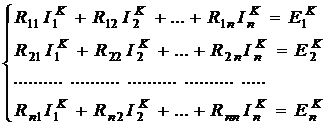(1.1)

где – собственное сопротивление n-го контура;

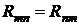– сопротивление ветви, общей для контуров n и m (межконтурное или общее сопротивление);

– контурный ток n-го контура;

– контурная ЭДС.

Система уравнений по методу узловых потенциалов имеет такую каноническую форму записи:

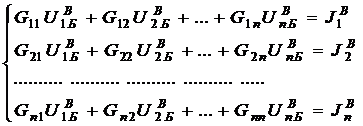(1.2)

где – собственная проводимость п-го узла;

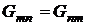– взаимная проводимость;

– межузловое напряжение между n-м и базовым узлами;

– «узловой» ток.

На рис. 1.1 указанные положительные направления токов в ветвях, положительные направления контурных токов, номера узлов. Исследование электрической цепи проводится бригадами в соответствии со своим вариантом. Варианты параметров элементов исследуемой схемы приведены в табл. 1.1.

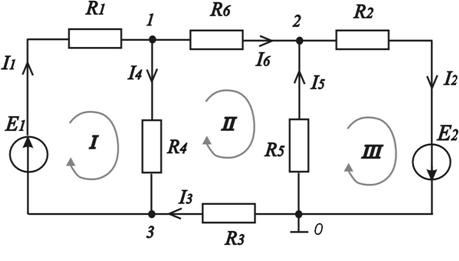
Рисунок 1.1 – Электрическая схема исследуемой цепи

Таблица 1.1– Варианты параметров элементов

1.3 Описание лабораторной установки

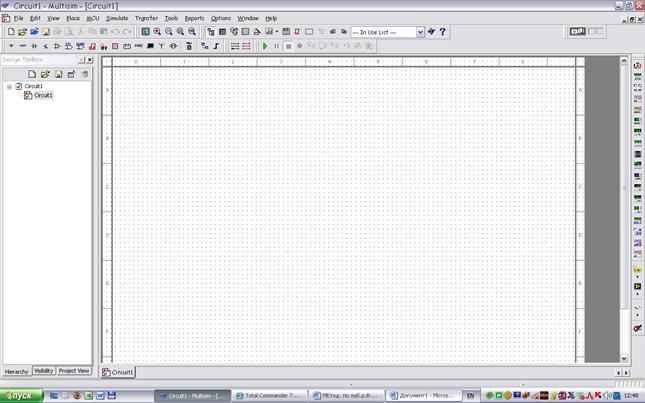
Главное окно прикладного пакета Multisim Education Edition 10.1.197 изображено на рис. 1.2.

Рисунок 1.2 – Внешний вид главного окна программы
Multisim Education Edition 10.1.197

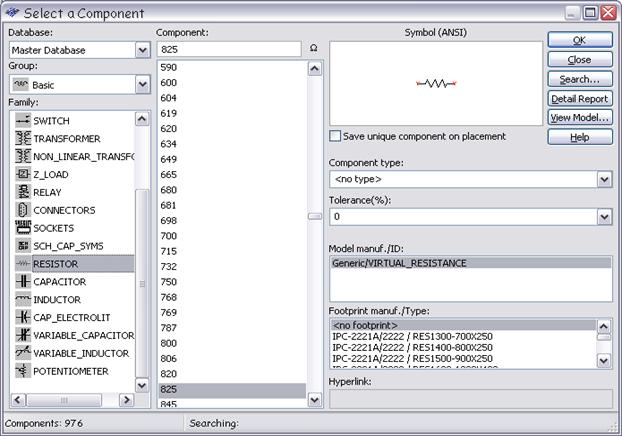
При нажатии на любую пиктограмму на панели выбора компонентов появляется окно выбора компонентов (рис. 1.3).

Рисунок 1.3 – Внешний вид окна выбора компонентов

Таким образом, для создания любой схемы электрической цепи нужно выбрать группу компонентов (например, BASІС), потом семейство компонентов (например, RESІSTOR), потом номинал или тип выбранного компонента (например, 825 Ом) и разместить элемент на рабочем поле. Как только элемент размещен, снова появляется окно выбора компонентов.

Для более простого перехода между группами компонентов удобно пользоваться списком выбора группы компонентов в соответствующем окне (рис. 1.4), которое по смыслу тождественно панели выбора группы компонентов.

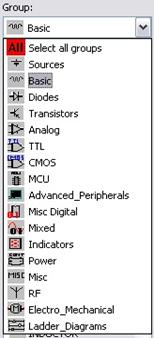
Рисунок 1.4 – Список выбора группы компонентов

Рассмотрим некоторые группы компонентов и компоненты которые к ним принадлежат:

·  группа SOURCES (рис. 1.5). К ней принадлежат разнообразные источники питания, источники тока, источники напряжения, общий провод (земля).

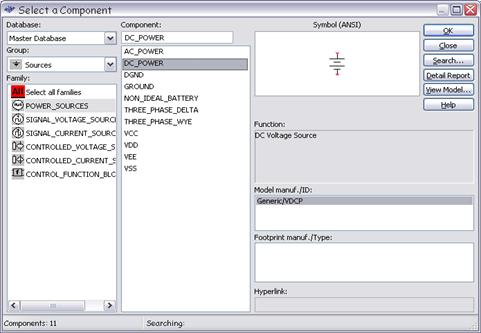
Рисунок 1.5 – Окно выбора семейства компонентов группы SOURCES

·  группа BASIC (рис. 1.6). К ней принадлежат простейшие элементы, такие, как резисторы (семейство RESІSTOR), конденсаторы (семейство CAPACІTOR), катушки индуктивности (семейство ІNDUCTOR), трансформаторы (семейство TRANSFORMER), переключатели (семейство SWІCH) и прочее.

·   

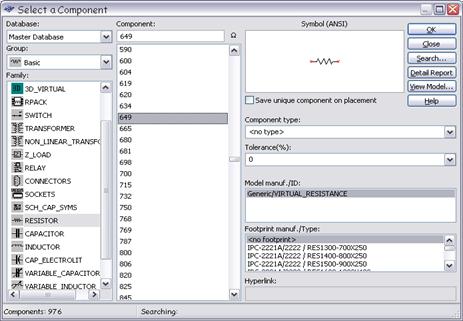
Рисунок 1.6 – Окно выбора семейства компонентов группы BASIC

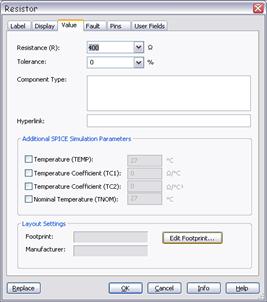
Рисунок 1.7 – Свойства компонента RESISTOR

Если при выборе резистора в окне выбора номинала элемента нет необходимого номинала, то нужно избрать наиболее близкий по значению, установить его на рабочем поле. После этого нажать на нем правой кнопкой мышки и зайти в пункт меню Propertіes (рис. 1.7). В закладке Value в графе Resіstance (R) указать точное значение сопротивления резистора в Омах. Другие графы оставить без изменений.

1.4 Порядок выполнения работы и методические указания относительно ее выполнения

1.4.1 Измерение токов в ветвях

1.4.1.1 Собрать схему согласно рис. 1.8 с номиналами элементов по вариантам, согласно табл. 1.1.

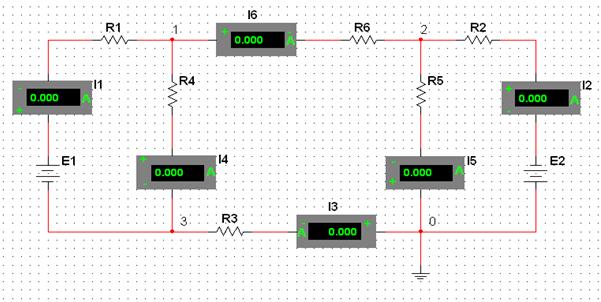
Рисунок 1.8 – Схема измерения токов в ветвях

Компонент резистор находится в группе BASІС, семейство RESІSTOR. Для измерения токов в ветвях необходимо к каждой ветви подключить амперметр, который находится в группе ІNDІCATORS, семейство AMMETER. Нужно придерживаться направлений токов, как показано на рис. 1.1. Для этого нужно "+" клемму амперметра подключать с той стороны, откуда течет ток, а "–" клемму амперметра со стороны, куда течет ток. Для соединения между собой элементов схемы нужно привести курсор мышки на край контакта любого элемента. Курсор будет иметь вид . После этого нажать правую кнопку мышки, провести линию к краю контакта следующего элемента схемы так, чтобы курсор мышки стал красным, и нажать ее правую кнопку. Если соединение проведено успешно, на рабочем поле появится проводник. Когда схема полностью собрана, необходимо начать симуляцию с помощью выключателя симуляции в верхнем правом углу окна программы (рис. 1.2). Провести измерение токов во всех ветвях. Результаты записать к табл. 1.2.

Таблица 1.2 – Экспериментальные данные измерения токов в ветвях

1.4.1.2 Измерить частичные токи в ветвях при действии каждой из ЭДС отдельно, придерживаясь направлений токов в этих ветвях, как показано на рис. 1.1. Токи в ветвях исследуемой электрической цепи формируются благодаря двум источникам ЭДС. Если измерить частичные токи при действии сначала одного источника ЭДС, потом второго и сложить эти значения с учетом знака, то получим значение токов в ветвях. Для исследования частичных токов собрать схему согласно рис. 1.9 и рис. 1.10.

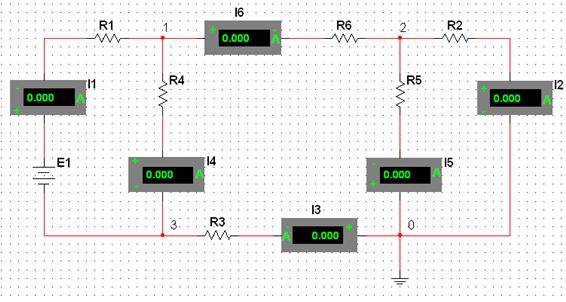
Рисунок 1.9 – Схема для измерения частичных токов (при действии Е1)

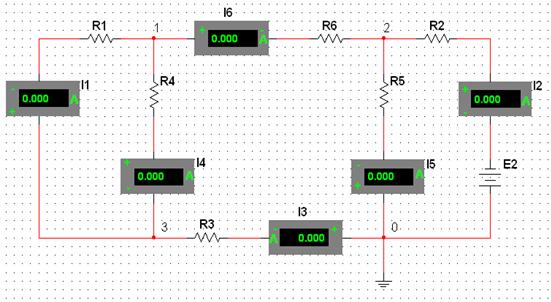
Рисунок 1.10 – Схема для измерения частичных токов (при действии Е2)

Измерение частичных токов в ветвях провести аналогично п. 1.4.1.1. Обратить внимание, какие частичные токи при направлениях, указанных на рис. 1.1, могут иметь отрицательные значения. Данные измерений с учетом знака измеренной величины внести в табл. 1.3.

Таблица 1.3 – Экспериментальные данные измерения частичных токов в ветвях

1.4.2 Измерение межузловых напряжений

Измерение межузловых напряжений проводится между узлами 0, 1, 2, 3, которые обозначены на рис. 1.1. За базовый узел принимается 0. Подключать три вольтметра к узлам 1, 2, 3 таким образом, чтобы "–" клемму подключить к базовому узлу 0, а "+" клемму к узлам 1, 2, 3 (рис. 1.11). Таким образом измерить межузловые напряжения , , . Данные измерений с учетом знака внести в табл. 1.4.

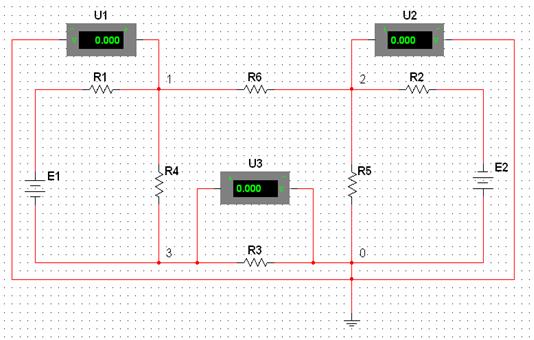
Рисунок 1.11 – Схема для измерения межузловых напряжений

Таблица 1.4 – Результаты измерений межузловых напряжений

1.4.3 Измерение напряжения холостого хода

В указанной преподавателем ветви цепи изъять резистор и записать величину его сопротивления (для примера это будет резистор ). На место отключенного резистора подключить вольтметр и измерить напряжение холостого хода в разомкнутой ветви цепи (рис. 1.12).

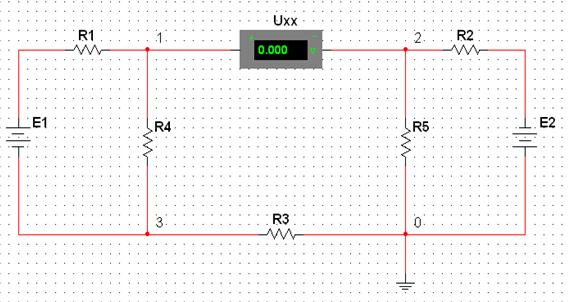
Рисунок 1.12 – Пример схемы для измерения напряжения холостого хода

в ветви с резистором

1.4.4 Измерение тока короткого замыкания

В той же ветви цепи, где изъят резистор , измерить ток короткого замыкания . Для этого вместо вольтметра на место изъятого резистора подключить амперметр в разомкнутую ветвь цепи (рис. 1.13).

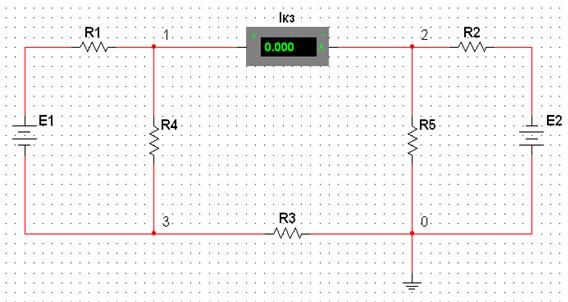
Рисунок 1.13 – Пример схемы для измерения тока короткого замыкания в ветви с резистором

1.4.5 Обработка результатов измерений

1.4.5.1 Рассчитать полные токи в ветвях, используя данные измерений частичных токов за гг. 1.4.1.2. Полные токи рассчитываются по методу наложения. Дополнить табл. 1.3 результатами расчетов полных токов.

1.4.5.2 Рассчитать внутреннее сопротивление эквивалентного генератора по п. 1.4.3 и 1.4.4 как 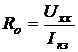. Рассчитать ток в заданной ветви цепи, используя метод эквивалентного генератора:

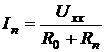. (1.3)

Для ветви с резистором формула будет иметь вид .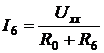

1.4.6 Теоретический расчет параметров цепи

Теоретический расчет параметров исследуемой электрической цепи проводится методами контурных токов и межузловых напряжений, которые базируются на составлении и решении систем алгебраических уравнений.

1.4.6.1 Рассчитать токи в ветвях методом контурных токов. С этой целью составить систему уравнений (1.1), в которой определить собственные и общие сопротивления и контурные ЭДС (по варианту, табл. 1.1). Решить систему уравнений и определить токи в ветвях по полученным значениям контурных токов. Дополнить табл. 1.2 столбцом расчетов по методу контурных токов.

1.4.6.2 Рассчитать токи в ветвях методом межузловых напряжений, взяв нулевой узел за базовый (см. рис. 1.1). С этой целью составить систему уравнений (1.2), в которой определить собственные и взаимные проводимости и узловые токи (по вариантам, табл. 1.1). Решить систему уравнений и определить межузловые напряжения, дополнить табл. 1.4 столбцом расчетных значений. По рассчитанным значениям межузловых напряжений определить токи в ветвях цепи по закону Ома. Дополнить табл. 1.2 столбцом расчетов методом межузловых напряжений.

1.4.7 Сравнение экспериментальных и теоретических результатов

1.4.7.1 По данными табл. 1.2 сравнить экспериментальные значения токов с данными теоретических расчетов, объяснить расхождение между теоретическими и экспериментальными данными.

1.4.7.2 Для заданного преподавателем узла проверить выполнение первого закона Кирхгофа по экспериментальным значениям токов (табл. 1.2).

1.4.7.3 Сравнить результаты расчетов двумя теоретическими методами: контурных токов и межузловых напряжений. Объяснить причины расхождения между данными, если они есть.

1.4.7.4 Сравнить экспериментальные данные измерений токов по табл. 1.2 и результат их расчета по методу наложения (табл. 1.3), объяснить расхождение между этими данными.

1.4.7.5 По данным табл. 1.4 сравнить экспериментальные значения межузловых напряжений с данными теоретических расчетов, объяснить расхождение между теоретическими и экспериментальными данными.

1.4.7.6 Сравнить значение тока в заданной ветви цепи, рассчитанного методом эквивалентного генератора (1.1), со значением этого же тока в табл. 1.2.

1.5 Содержание отчета

Отчет должен содержать:

– название работы;

– цель работы;

– схему электрическую принципиальную исследуемой цепи с обозначенными направлениями токов в ветвях, контурных токов и узлов;

– данные варианта параметров исследуемой цепи из табл. 1.1.;

– результаты измерений по п. 1.4.2 – 1 .4.4;

– данные обработки результатов измерений по п. 1.4.5;

– данные теоретических расчетов по п. 1.4.6;

– выводы по п. 1.4.7.

1.6 Контрольные вопросы и задачи

1. Дайте определение ЭДС, напряжения, падение напряжения, тока.

2. Запишите закон Ома для пассивного и активного участков цепи.

3. Сформулируйте первый и второй законы Кирхгофа. Укажите порядок расчета цепи методом уравнений Кирхгофа.

4. В чем суть принципа наложения и расчета цепи методом наложения?

5. Объясните сущность метода контурных токов и метода межузловых напряжений.

6. Изложите порядок расчета цепи методом эквивалентного генератора.

7. Как определяются собственное и общее сопротивление?

8. Как определяется узловая и межузловая проводимость?

9. По какими критериями определяется оптимальный метод расчета электрической цепи?

10. Проанализируйте заданную преподавателем электрическую цепь, применяя предложенный метод анализа.

2 ИССЛЕДОВАНИЕ ПАРАМЕТРОВ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА

2.1 Цель работы

Целью работы является теоретическое и экспериментальное определения параметров пассивных элементов электрических цепей переменного тока. Расчет цепей переменного тока при последовательном и параллельном соединении резистора с катушкой индуктивности или конденсатором. Сравнение результатов измерений с расчетными данными.

2.2 Методические указания по организации самостоятельной работы студентов

Во время подготовки к лабораторной работе необходимо обработать теоретический материал из раздела "Линейные электрические цепи переменного тока", ознакомиться с содержанием лабораторной работы и подготовить бланк отчета.

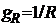В работе исследуются пассивные элементы (резистор, катушка индуктивности, конденсатор без потерь), которые включены в цепь переменного тока (рис. 2.1). В цепи переменного тока резистор характеризуется активным сопротивлением (или проводимостью ), катушка индуктивности характеризуется активным сопротивлением и реактивным сопротивлением , а конденсатор без потерь – реактивным сопротивлением .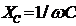

Полное сопротивление катушки индуктивности определяется так

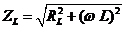, (2.1)

модуль проводимости

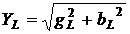, (2.2)

где 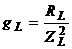– активная составляющая проводимости;

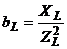– реактивная составляющая проводимости.

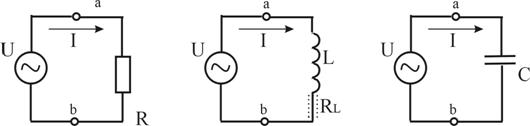
Рисунок 2.1 – Пассивные элементы в цепи переменного тока

Модуль комплексного сопротивления конденсатора без потерь определяется как

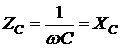, (2.3)

модуль проводимости

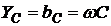, (2.4)

где – реактивная составляющая проводимости.

В комплексной форме полное сопротивление резистора равняется активному сопротивлению, т. е. .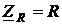

Комплексное сопротивление катушки индуктивности равняется

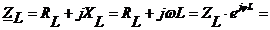
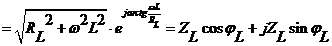(2.5)

В формуле (2.5) угол сдвига фаз между током и напряжением для катушки определяется так

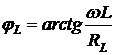. (2.6)

Комплексное сопротивление конденсатора без потерь равняется его реактивному сопротивлению

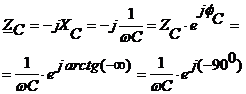, (2.7)

где 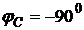– угол сдвига фаз между напряжением и током для конденсатора без потерь.

В данной лабораторной работе применяется символический метод описания величин тока, напряжения и сопротивления как комплексных функций. Например, ток синусоидальной формы 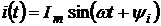подается в комплексной форме как комплексная функция действующей величины тока 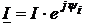, где принимается, что .

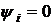Падение напряжения на пассивных элементах цепи (резисторе, катушке индуктивности, конденсаторе) при действии синусоидального тока и заданных параметрах элементов определяется по закону Ома. Комплексные значения действующих напряжений на исследуемых пассивных элементах определяются так

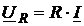; (2.8)

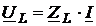; (2.9)

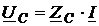. (2.10)

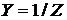Полное сопротивление и проводимость цепи при известных значениях тока, напряжения и угла сдвига фаз можно определить так

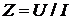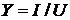; , (2.11)

а их активная и реактивная составляющая определяются так

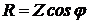; (2.12)

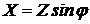; (2.13)

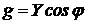; (2.14)

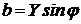. (2.15)

В работе исследуется последовательное соединение резистора с катушкой индуктивности или конденсатором (рис. 2.2).

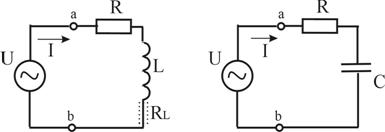
Рисунок 2.2 – Последовательные – и – цепи

Модуль комплексного сопротивления последовательного соединения резистора и катушки индуктивности определяется так

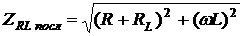. (2.16)

Модуль комплексного сопротивления последовательного соединения резистора и конденсатора без потерь определяется так

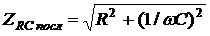(2.17)

Комплексное сопротивление последовательного соединения резистора и катушки индуктивности равняется

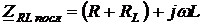. (2.18)

Угол сдвига фаз между напряжением и током для последовательного соединения резистора и катушки определяется так

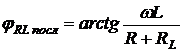. (2.19)

Комплексное сопротивление последовательного соединения резистора и конденсатора без потерь равняется

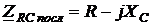(2.20)

Угол сдвига фаз между напряжением и током для последовательного соединения резистора и конденсатора определяется так

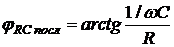. (2.21)

Падение напряжения на исследуемом последовательном участке цепи при заданном токе и параметрах элементов рассчитывается так

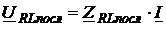; (2.22)

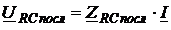(2.23)

Полное сопротивление при известных значениях тока, напряжения и угла сдвига фаз можно определить по (2.11), а активную и реактивную составляющую сопротивления – по (2.12, 2.13).

В работе исследуется параллельное соединение резистора с катушкой индуктивности или конденсатором (рис. 2.3).

Во время анализа цепей с параллельным соединением элементов удобно перейти от понятия "сопротивление" к понятию "проводимость".

Рисунок 2.3 – Параллельные – и – цепи

Модуль комплексной проводимости параллельного соединения резистора и катушки индуктивности определяется так (см. п. 2.2.1)

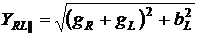. (2.24)

Модуль комплексной проводимости параллельного соединения резистора и конденсатора без потерь определяется так:

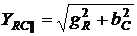. (2.25)

Комплексная проводимость параллельного соединения резистора и катушки индуктивности равняется

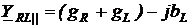. (2.26)

Угол сдвига фаз между напряжением и током для параллельного соединения резистора и катушки определяется так:

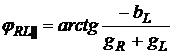. (2.27)

Комплексная проводимость параллельного соединения резистора и конденсатора равняется

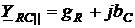. (2.28)

Угол сдвига фаз между напряжением и током для параллельного соединения резистора и конденсатора определяется по формуле:

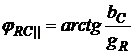. (2.29)

Падение напряжения на исследуемом параллельном участке цепи при заданном токе и параметрах элементов рассчитывается так:

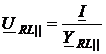; (2.30)

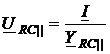. (2.31)

Полная проводимость при известных значениях тока, напряжения и угла сдвига фаз можно определить по (2.11), а активную и реактивную составляющую сопротивления – по (2.14) и (2.15).

Исследование электрических цепей (рис. 2.1-2.3) проводится бригадами по вариантам. Варианты параметров элементов и параметров входного сигнала приведены в табл. 2.1.

Таблица 2.1 – Варианты задач

2.3 Описание лабораторной установки

Для выполнения лабораторной работы необходимо в окне выбора компонентов в группе BASІС найти резистор (семейство RESІSTOR), конденсатор (семейство CAPASІTOR) и индуктивность (семейство ІNDUCTOR) с номиналами согласно варианту. Как источник питания следует использовать источник AC_POWER, который находится в группе SOURCES, семейство POWER_SOURCES. В свойствах элемента AC_POWER выставить данные, согласно варианту (рис. 2.4): Voltage (RMS) – 10 В, Frequency (F) – 400 Гц.

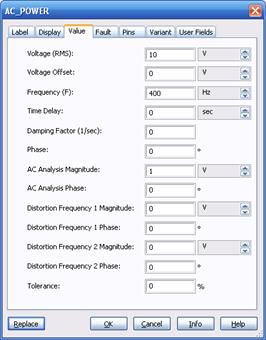
Рисунок 2.4 – Окно компонента качества источника питания AC_POWER

Для определения угла сдвига фаз между напряжением и током в цепи следует использовать на панели выбора инструментов для измерения такие приборы, как Oscіlloscope и Bode Plotter по схемам на рис. 2.6-2.11. С помощью Oscіlloscope можно визуально наблюдать сдвиг фаз между напряжением и током, а с помощью Bode Plotter – получить численное значение угла сдвига фаз . В свойствах компонента Bode Plotter необходимо в поле Mode выбрать Phase, в поле Horizontal выбрать значение F=1GHz – максимальное значение частоты, І=400Hz – минимальное значение частоты (рис. 2.5).

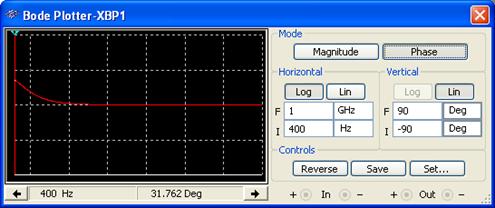
Рисунок 2.5 – Окно компонента Bode Plotter

2.4 Порядок выполнения работы

Лабораторная работа включает такие виды работ: экспериментальные исследования цепей (рис. 2.6-2.11), обработка результатов эксперимента, теоретические расчеты параметров цепей и сравнительный анализ результатов.

Все экспериментальные исследования и теоретические расчеты проводятся при одинаковых параметрах входного сигнала (частота сигнала f = 400 Гц, входное напряжение U = 10 В).

2.4.1 Экспериментальные исследования

Исследуемые электрические цепи переменного тока состоят из последовательно соединенных источника сигнала низкой частоты, амперметра, участка цепи с нагрузкой и вспомогательного резистора R=1 Ом. В качестве нагрузки поочередно подключаются отдельные пассивные элементы C и L или участки цепи, в которых эти элементы соединены последовательно или параллельно.

Заданием эксперимента являются измерения падения напряжения на нагрузке и угла сдвига фаз между напряжением и током в цепи, при этом начальная фаза тока принимается нулевой.

Измерение действующего напряжения на исследуемых элементах проводится вольтметром. Измерение угла сдвига фаз проводится с помощью Bode Plotter при подаче на клеммы опорного напряжения (с выхода генератора) и сигнального напряжения (с дополнительного резистора R).

2.4.1.1 Исследование катушки индуктивности

Выполнить монтаж схемы (рис. 2.6), подключив катушку индуктивности и резистор RL (внутреннее сопротивление катушки индуктивности) с номиналами согласно варианту и вспомогательный резистор R=1 Ом. После проверки схемы преподавателем задать параметры входного сигнала, регулируя частоту и напряжение в составленной цепи. Провести измерение величины Івх, и с помощью вольтметра и с помощью компонента Bode Plotter-XBP1. С помощью Oscіlloscope-XSC1 исследовать форму напряжения и сдвиг фаз между напряжением и током. Результаты внести в табл. 2.2.

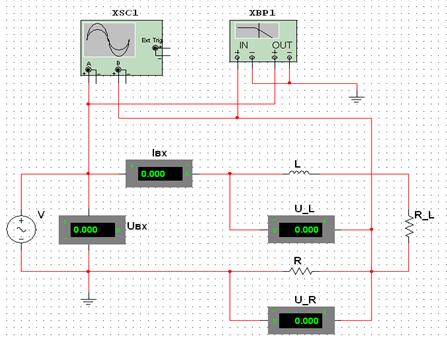
Рисунок 2.6 – Экспериментальная схема для исследования катушки индуктивности

Таблица 2.2 – Результаты измерений при исследовании катушки индуктивности

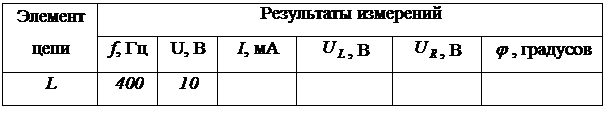
2.4.1.2 Исследование конденсатора

Выполнить монтаж схемы (рис. 2.7), подключив конденсатор с номиналом согласно варианту и вспомогательный резистор R=1 Ом. Провести измерение величины Івх, и с помощью вольтметра и с помощью компонента Bode Plotter-XBP1. С помощью Oscіlloscope-XSC1 исследовать форму напряжения и сдвиг фаз между напряжением и током. Результаты внести в табл. 2.3.

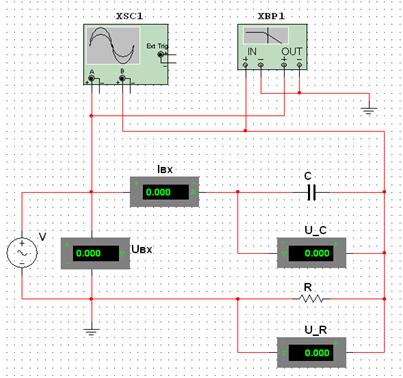
Рисунок 2.7 – Экспериментальна схема для исследования конденсатора

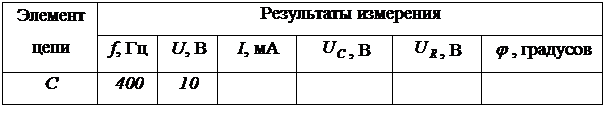Таблица 2.3 – Результаты измерений при исследовании конденсатора

2.4.1.3 Исследование последовательного соединения катушки индуктивности и резистора

Составить схему (рис. 2.8), подключив последовательный участок цепи с катушкой индуктивности L, резистором RL и резистором R1 с номиналами согласно варианту. Номинал резистора R=1 Ом. Провести измерение величины с помощью вольтметра и 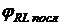с помощью компонента Bode Plotter-XBP1. С помощью Oscіlloscope-XSC1 исследовать форму напряжения и сдвиг фаз между напряжением и током. Результаты внести в табл. 2.4.

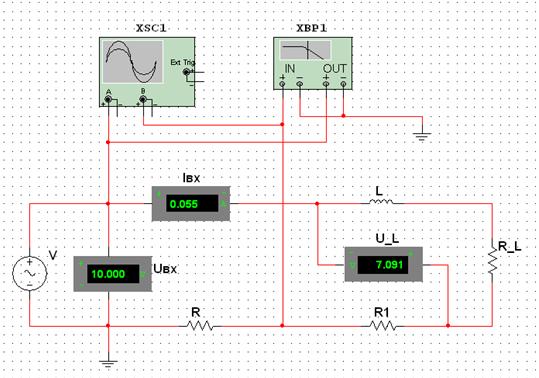
Рисунок 2.8 – Экспериментальная схема для исследования

последовательного соединения резистора и катушки индуктивности

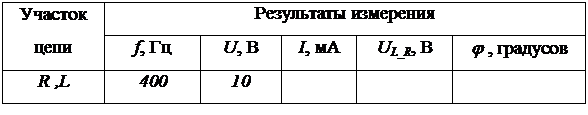Таблица 2.4 – Результаты измерений при исследовании последовательного соединения резистора и катушки индуктивности

2.4.1.4 Исследование последовательного соединения конденсатора и резистора

Составить схему (рис. 2.9), подключив последовательный участок цепи с резистором R1 и конденсатором С. Номинал резистора R=1 Ом. Провести измерение величины 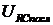с помощью вольтметра и с помощью Bode Plotter-XBP1. С помощью Oscіlloscope-XSC1 исследовать форму напряжения и сдвиг фаз между напряжением и током. Результаты внести в табл. 2.5.

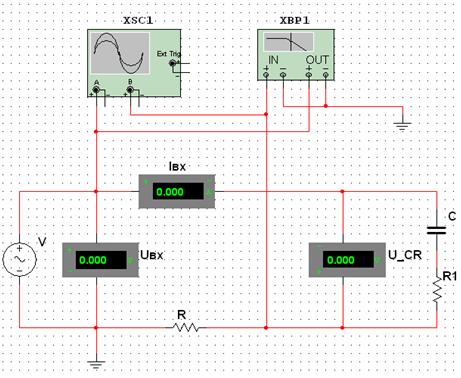
Рисунок 2.9 – Экспериментальная схема для исследования последовательного соединения конденсатора и резистора

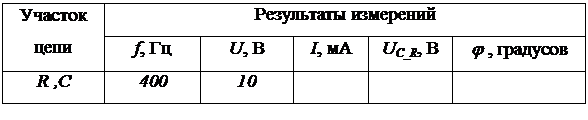Таблица 2.5 – Результаты измерений при исследовании последовательного соединения резистора и конденсатора

2.4.1.5 Исследование параллельного соединения катушки индуктивности и резистора

Выполнить монтаж схемы (рис. 2.10), собрав параллельный участок цепи с катушкой индуктивности L, резистором RL и резистором R1 с номиналами согласно варианту. Номинал резистора R=1 Ом. Провести измерение величины , с помощью амперметров и с помощью Bode Plotter-XBP1. С помощью Oscіlloscope-XSC1 исследовать форму напряжения и сдвиг фаз между напряжением и током. Результаты внести в табл. 2.6.

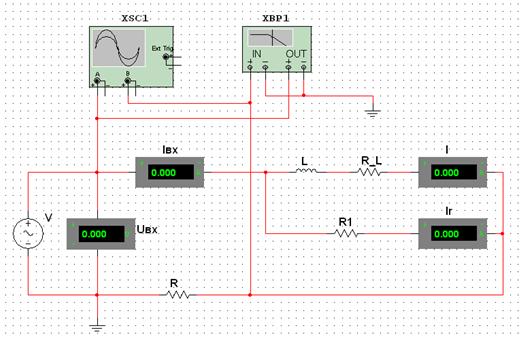
Рисунок 2.10 – Экспериментальная схема для исследования параллельного соединения катушки индуктивности и резистора

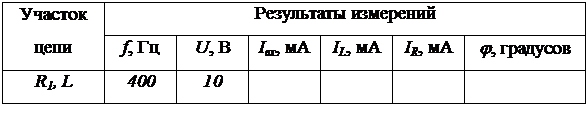Таблица 2.6 – Результаты измерений при исследовании параллельного соединения катушки индуктивности и резистора

2.4.1.6 Исследование параллельного соединения конденсатора и резистора

Выполнить монтаж схемы (рис. 2.11), собрав параллельный участок цепи с катушкой индуктивности L, резистором RL и резистором R1 с номиналами согласно варианту. Номинал резистора R=1 Ом. Провести измерение величины , с помощью амперметров и с помощью Bode Plotter-XBP1. С помощью Oscіlloscope-XSC1 исследовать форму напряжения и сдвиг фаз между напряжением и током. Результаты внести в табл. 2.7.

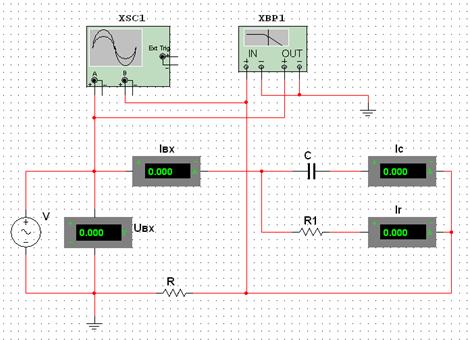
Рисунок 2.11 – Экспериментальная схема для исследования параллельного

соединения конденсатора и резистора

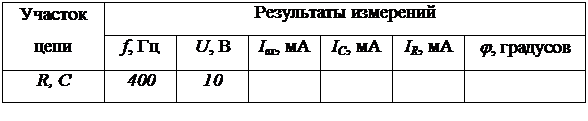Таблица 2.7 – Результаты измерений при исследовании
параллельного соединения конденсатора и резистора

2.4.1.7 По результатам измерений (2.4.1.5, 2.4.1.6) построить векторные диаграммы для последовательного и параллельного участков цепи.

2.4.2 Расчет результатов экспериментов

2.4.2.1 По результатам эксперимента (п2.4.1.1) рассчитать параметры пассивных элементов цепи, используя данные эксперимента, по формулам, указанных в табл. 2.8. Учитывать, что ω=2πf. Результаты расчетов записать в соответствующие ячейки табл. 2.8.

Таблица 2.8 – Результаты расчетов параметров пассивных элементов

2.4.2.2 По результатам эксперимента (п2.4.1.2) рассчитать параметры последовательной RL и RC участков цепи, пользуясь данными эксперимента, по формулам, указанными в табл. 2.9. Результаты расчетов записать в соответствующие ячейки табл. 2.9.

Таблица 2.9 – Результаты расчетов параметров последовательного соединения элементов

2.4.3 Теоретические расчеты параметров цепи

Теоретический расчет параметров последовательной и параллельной участков цепи предусматривает расчет действующего значения напряжения U и угол сдвига фаз j по заданному варианту (табл. 2.1) параметрами элементов R, L, RL, C при заданном токе I=20 мА.

2.4.3.1 Рассчитать параметры последовательного RL и RC участков цепи по формулам, указанными в табл. 2.10. Результаты расчетов записать в соответствующие ячейки табл. 2.10.

Таблица 2.10 – Теоретические расчеты параметров последовательного соединения элементов

2.4.3.2 Рассчитать параметры параллельного RL и RC участков цепи по формулам, указанными в табл. 2.11. Результаты расчетов записать в соответствующие ячейки табл. 2.11.

Таблица 2.11 – Теоретические расчеты параметров параллельного соединения элементов

2.4.4 Сравнительный анализ результатов

2.4.4.1 Сравнить параметры пассивных элементов цепи по варианту (см. табл. 2.1) и полученные по данным экспериментов (табл. 2.8).

2.4.4.2 Сравнить параметры последовательного участка цепи данных эксперимента (табл. 2.9) с результатами теоретических расчетов (табл. 2.11).

2.4.4.3 Сравнить параметры параллельного участка цепи данных эксперимента (табл. 2.9) с результатами теоретических расчетов (табл. 2.11).

2.4.4.4 Сравнить полученные значения напряжения и угла сдвига фаз (табл.2.3,2.4) с соответствующими расчитаными значениями (табл. 2.10, 2.11).

2.5 Содержание отчета

Отчет должен содержать:

– название работы;

– цель работы;

– данные варианта задачи;

– схемы электрические принципиальные исследуемых цепей;

– осциллограммы;

– результаты расчетов;

– выводы.

2.6 Контрольные вопросы и задания

1. Как определяется активное, реактивное и полное сопротивления участка цепи?

2. Как определяется полное сопротивление участка цепи с последовательным соединением активного и реактивного элементов?

3. Как определяется полное сопротивление участка цепи с параллельным соединением активного и реактивного элементов?

4. Как определяется угол сдвига фаз между напряжением и током в цепи по параметрам пассивных элементов цепи?

5. Как определяется модуль полного сопротивления цепи по параметрам пассивных элементов цепи?

6. Как соотносятся полное сопротивление цепи и полная проводимость цепи, их активные и реактивные составные?

3 ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНОЙ RLC – ЦЕПИ ПЕРЕМЕННОГО ТОКА

3.1 Цель работы

Целью работы является экспериментальное исследование частотных характеристик RLC – цепи переменного тока. Изучение явления резонанса напряжения. Сравнение частотных характеристик цепи при различной добротности.

3.2 Методические указания по организации самостоятельной работы студентов
Во время подготовки к лабораторной работе необходимо обработать теоретический материал из разделов «Частотные свойства цепей переменного тока» и «Резонансные явления в линейных электрических цепей переменного тока». Ознакомиться с содержанием лабораторной работы и подготовить бланк отчета.

В работе исследуются пассивные элементы (резистор, катушка индуктивности, конденсатор), которые последовательно включены в цепь переменного тока (рис. 3.1). Катушка индуктивности изображена в виде последовательно соединенных резисторов RK и индуктивности L (на рис. 3.1 обведена пунктиром).

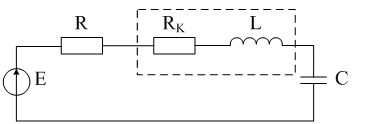
Рисунок 3.1 – Последовательный RLC – контур

Основные параметры последовательного RLC – контура определяются следующим образом:

– полное комплексное сопротивление

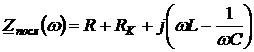, (3.1)

– модуль комплексного сопротивления

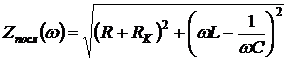, (3.2)

– модуль действующего значения тока при заданном напряжении

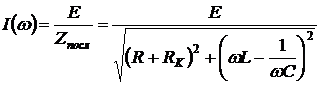, (3.3)

– угол сдвига фаз между током и напряжением

. (3.4)

Функции 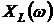, 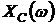являются частотными характеристиками (ЧХ) реактивных элементов (рис. 3.2).

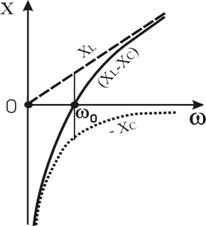
Рисунок 3.2 – Частотные характеристики реактивной составляющей сопротивления RLC – контура

Функции , , 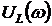называются амплитудно-частотными характеристиками (АЧХ) RLC – контура. В работе исследуется АЧХ и АЧХ 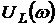, , 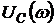которые описываются следующим образом

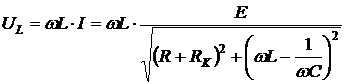, (3.5)

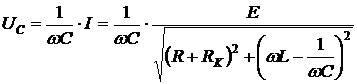. (3.6)

Функция (3.4) является фазочастотной характеристикой (ФЧХ) RLC – контура. Графики АЧХ и ФЧХ последовательного RLC – контура приведены на рис. 3.3.

В цепи с разнородными реактивными элементами возможно явление резонанса напряжений или токов. В последовательном RLC – контуре возникает резонанс напряжений при условии равенства нулю реактивной составляющей полного сопротивления цепи (3.1), тоесть 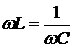, откуда резонансная круговая частота определяется следующим образом

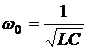, (3.7)

или

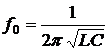. (3.8)

В режиме резонанса напряжений полное сопротивление цепи минимально и равно его активной составляющей, то есть 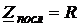, тогда угол сдвига фаз 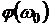равен нулю. В этих условиях ток в цепи (3.3) достигает максимального значения 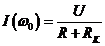(см. рис. 3.3).

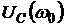При резонансе напряжения на индуктивном (3.5) и емкостной (3.6) элементах равны по значению (см. рис. 3.3), но противоположные по фазе, поэтому они компенсируют друг друга.

При резонансе напряжений происходит «переворот фаз»
(см. рис. 3.3), поскольку при частоте ниже резонансной цепь имеет емкостный характер (), при частоте выше резонансной – индуктивный характер ().

При резонансе RLC – контур характеризуется дополнительными параметрами:

– характеристическим (волновым) сопротивлением контура

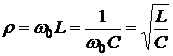, (3.9)

– добротностью

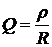. (3.10)

Когда 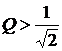, то напряжения на реактивных элементах для частот, близких к резонансной, превышают входное напряжение.

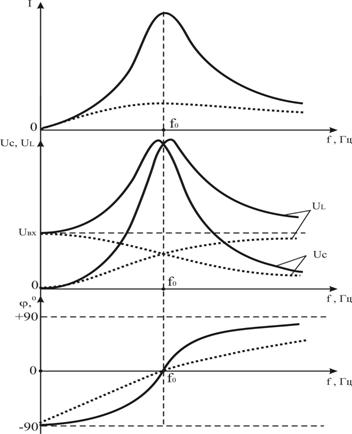
Рисунок 3.3 – АЧХ и ФЧХ последовательного RLC – контура: непрерывные кривые – при , пунктирные кривые – при

Исследование последовательного RLC – контура (рис. 3.1) проводится бригадами по вариантам. Варианты параметров реактивных элементов и входного сигнала приведены в табл. 3.1.

Таблица 3.1 – Варианты заданий

В лабораторной работе используется источник переменного напряжения. Для измерений напряжений на реактивных элементах используются вольтметры переменного тока; для измерения тока – амперметр переменного тока; для измерения угла сдвига фаз – графостроитель (Body Plotter).

3.3 Порядок выполнения работы и методические указания по ее выполнению

Лабораторная работа включает экспериментальное и6сследование частотных характеристик RLC – контура, теоретические расчеты параметров цепи при резонансе напряжений и сравнительный анализ частотных характеристик при различных значениях активного сопротивления цепи.

Все экспериментальные исследования проводятся при одинаковой величине входного сигнала (по варианту табл. 3.1) на разных частотах.

3.3.1 Экспериментальные исследования

Исследуемая электрическая цепь переменного тока состоит из последовательно соединенных источника синусоидального сигнала, амперметра, последовательной RLC – участка цепи (рис. 3.4).

Задачей эксперимента является измерение падения напряжений на реактивных элементах цепи, угла сдвига фаз между током и напряжением в цепи, тока в цепи при различных значениях частоты входного сигнала.

Измерение угла сдвига фаз производится при подаче на клеммы графостроителя сигналов с выхода источника переменного тока и сигнальной напряжения. Начальная установка параметров для измерения угла сдвига фаз с помощью графостроителя осуществляется следующим образом.

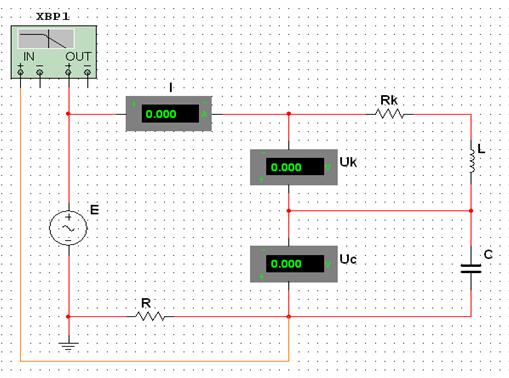
Рисунок 3.4 – Экспериментальная схема для исследования частотных характеристик RLC – контура

Открыть окно графостроителя, нажав на нем левую кнопку мышки два раза. Нажать кнопку PHASE. По шкале X (HORIZONTAL) установить максимальное (F) и минимальное (I) значение частоты (3 кГц и 50 Гц). По шкале Y (VERTICAL) установить максимальное (F) и минимальное (I) значения измеряемой фазы (90º и -90º).

Нажать кнопку включения источника. На экране графостроителя появится значение частоты и фазы согласно положению маркеров. Установить фазу -75º и измерить значение частоты. Выключить питание схемы и установить это значение частоты на источнике питания. Включить снова питание схемы и записать в табл. 3.2 значения I, UL, UC для этого значения фазы.

Установить с помощью маркера (грубо) и кнопок и (точно) новое значение фазы (-60º). Записать значение частоты в табл. 3.2 и выключив электрическую цепь, установить это значение на источнике питания. Включить цепь и записать значение I, UL, UC в табл. 3.2.

Таким образом, повторяем эти действия до полного заполнения табл.3.2.

1) Исследовать частотные характеристики RLC – контура. Создать схему (см. рис. 3.4), установив R = 10 Ом. После проверки схемы преподавателем установить величину ЭДС входного сигнала по варианту (табл. 3.1). Изменять фазу, пока она не будет равна около –60º. Записать значение f, I, UL, UC согласно табл. 3.2.

Таблица 3.2 – Результаты измерений

Повторить изменения фазы согласно табл. 3.2 к 75º.

Изменить значение R с 10 Ом на 100 Ом. Повторить эксперимент для нового значения R и заполнить новую таблицу по форме табл. 3.2.

Еще раз изменить R на 500 Ом и повторить эксперимент для нового значения R, заполнить третью таблицу по форме табл. 3.2.

2) Построить АЧХ и ФЧХ исследуемого RLC – контура для трех различных значений R.

3.3.2 Теоретические расчеты

1) рассчитать резонансную частоту последовательного RLC – контура (3.8) по данным варианта (табл. 3.1);

2) рассчитать характеристическое сопротивление контура , активное сопротивление контура 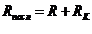и добротность для
R=10 Ом и R=500 Ом;

3) рассчитать значение тока при резонансе для R=10 Ом та
R=500 Ом;

4) рассчитать значения напряжений на реактивных элементах при резонансе 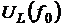и 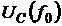для R=10 Ом и R=500 Ом.

3.3.3 Сравнительный анализ результатов

1) сравнить характер АЧХ тока в последовательном RLC – контуре при R=10 Ом и R=500 Ом. Объяснить влияние величины активного сопротивления на форму АЧХ;

2) сравнить характер АЧХ напряжений на реактивных элементах в последовательном RLC – контуре при R=10 Ом и R=500 Ом. Объяснить влияние величины активного сопротивления на форму АЧХ;

3) сравнить ФЧХ последовательного RLC – контура при R=10 Ом и

R=500 Ом. Объяснить влияние величины активного сопротивления на форму ФЧХ;

4) сравнить значение резонансной частоты, полученной экспериментально (п. 3.3.1, 1) и рассчитанной по п. 3.3.2, 1. Объяснить причину расхождения результатов;

5) сравнить значение тока при резонансе, полученные экспериментально и рассчитанные по п. 3.3.2, 3;

6) сравнить значения напряжений на реактивных элементах при резонансе, полученные экспериментально и рассчитанные по п. 3.3.2, 4.

3.4 Содержание отчета

Отчет должен содержать:

– название работы;

– цель работы;

– схему электрическую принципиальную изучаемой цепи;

– данные варианта параметров исследуемой цепи табл. 3.1;

– результаты экспериментальных исследований по п. 3.3.1;

– АЧХ и ФЧХ по п. 3.3.1;

– данные теоретических расчетов по п. 3.3.2;

– выводы по п. 3.3.3.

3.5 Контрольные вопросы и задания

1 В какой цепи может возникнуть резонанс?

2 Какое условие возникновения резонанса напряжений?

3 Какое условие возникновения резонанса токов?

4 Как определяется резонансная частота?

5 Какими параметрами определяется резонансная частота?

6 Что такое характеристическое сопротивление контура?

7 Что такое добротность контура?

8 Назовите экспериментальные признаки резонансного режима в контуре.

4 ИССЛЕДОВАНИЕ ТРЕХФАЗНОЙ ЦЕПИ ПРИ СОЕДИНЕНИИ ПРИЕМНИКОВ ЭНЕРГИИ ЗВЕЗДОЙ И ТРИУГОЛЬНИКОМ

4.1 Цель работы

Целью работы является исследование трехфазной цепи, подключенной к симметричной трехфазной системе ЭДС. Исследуется влияние сопротивления нейтрального провода при симметричной и несимметричной цепи, а также режим обрыва и короткого замыкания в одной из фаз трехфазной цепи.

4.2 Методические указания по организации самостоятельной работы студентов

При подготовке к выполнению лабораторной работы необходимо ознакомится с теоретическим материалом раздела «трехфазные цепи», содержанием лабораторной работы и подготовить бланк отчета.

В работе исследуются различные режимы работы трехфазной цепи при двух разновидностях соединения нагрузки – звездой и треугольником (рис. 4.1 и рис.4.2).

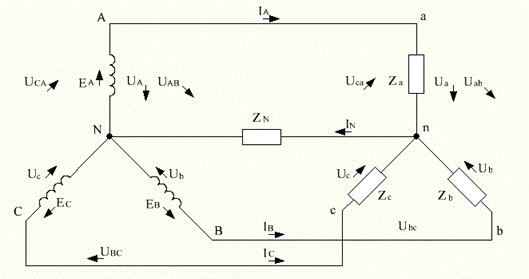
Рисунок 4.1 – Соединение приемника звездой

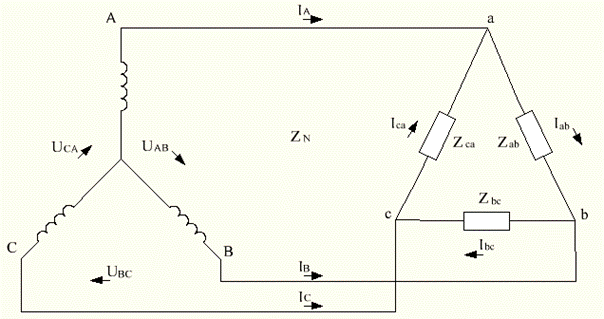Рисунок 4.2 – Соединение приемника треугольником

За условные положительные направления токов в линейных проводах принимают направления от источников к приемнику, а в нейтральном (нулевом) проводе – от приемника к источнику (см. рис. 4.1). Токи в фазах источника и приемника называются фазными, а токи в линейных проводах – линейными.

В линейном проводе и в последовательно соединенных с ним обмотках источника и приемника (рис. 4.1) протекает один и тот же ток, т. е. для данного соединения приемника линейный ток равен соответствующему фазному току

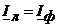(4.1)

В соответствии с выбранным условным положительным направлением фазных и линейных напряжений (рис 4.1):

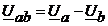
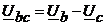(4.2)

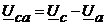
Данные уравнения позволяют определять линейные напряжения приемника по известным фазным напряжениям.

При соединении приемника треугольником видно, что фазные и линейные напряжения совпадают (рис. 4.2)

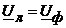(4.3)

а фазные и линейные токи не равны между собой.

Линейные токи определяют по фазным токам из уравнений, составленных по первому закону Кирхгофа для узлов a, b,c:

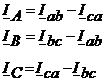(4.4)

Из уравнений (4.4) следует, что любой из линейных токов равен геометрической разности соответствующих векторов токов тех двух фаз приемника, которые соединяются с данным линейным проводом.

Трехфазная цепь может работать в двух режимах: симметричном и не симметричном.

4.2.1 Симметричный режим

Рассмотрим симметричный режим трехфазной цепи при соединении приемника звездой (рис. 4.1). Сопротивлением фазных обмоток генератора и соединительных проводов пренебрегаем. В этом случае фазные ЭДС равны фазным напряжениям:

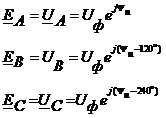(4.5)

Комплексы полных сопротивлений всех трех фаз одинаковы:

.

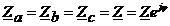При симметричном режиме нейтральные точки генератора и нагрузки (N, n) имеют один и тот же потенциал и согласно методу двух узлов:

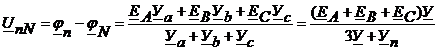(4.6)

где: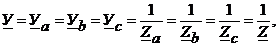

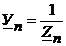
Так как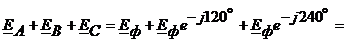

.

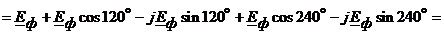
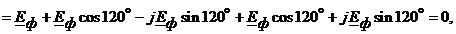
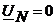Следовательно, фазные напряжения приемника будут равны фазным напряжениям источника:

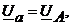
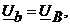
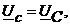
а токи в каждой фазе приемника равны

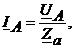
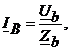
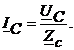(4.7)

И ток в нейтральном проводе

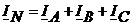
Из схемы (рис 4.1) видно, что при соединении фаз приемника звездой, фазные и линейные токи равны между собой.

При симметричной нагрузке токи в фазах согласно (4.5) и (4.7) равны по величине и сдвинуты по фазе на 120 , а их сумма равна нулю. Следовательно, равен нулю и ток нейтрального провода IN. Отсюда можно сделать вывод, что при симметричной нагрузке достаточно проводить расчет только для одной фазы и для подключения приемника нет необходимости использовать нейтральный провод.

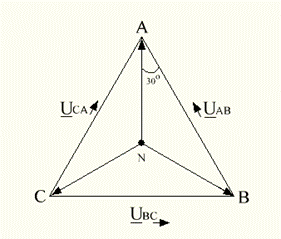Векторная диаграмма напряжений и токов для данной трехфазной цепи изображена на рис 4.3.

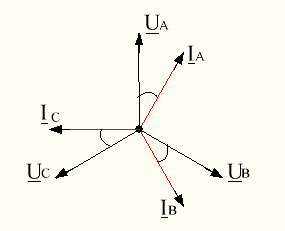
Рисунок 4.3 – Векторная Рисунок 4.4 – Векторная
диаграмма напряжений и токов диаграмма фазных и линейных

напряжений источника

На рис 4.4 в соответствии с (4.2) построена векторная диаграмма фазных и линейных напряжений источника при соединении его фаз звездой.

Соотношения между среднеквадратическими значениями фазных и линейных напряжений:

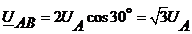
где UA – модуль фазного напряжения;

UAB – модуль линейного напряжения.

Следовательно, в симметричной системе напряжений при соединении в звезду:

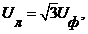
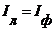(4.8)

Рассмотрим симметричный режим трехфазной цепи при соединении приемника треугольником (рис 4.2).

Из схемы видно, что при нулевых сопротивлениях линейных проводов, фазные напряжения приемника равны соответствующим линейным напряжениям источника

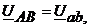
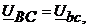
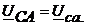
При заданных сопротивлениях приемника фазные токи равны:

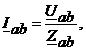
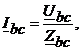
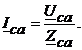(4.9)

Тогда в соответствии с (4.4) линейные токи равны:

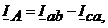
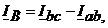
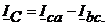
Векторная диаграмма напряжений и токов при симметричной нагрузке, соединенной треугольником, изображена на рис 4.5

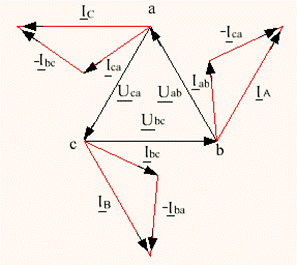
Рисунок 4.5 – Векторная диаграмма напряжений и токов
при симметричной нагрузке

При этом легко получить, что

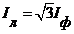(4.10)

Это соотношение справедливо только для симметричной нагрузки и в этом случае расчет токов можно производить только для одной фазы.

4.2.2 Несимметричный режим

Трехфазная цепь несимметрична, если комплексные сопротивления ее фаз не одинаковы.

Рассмотрим расчет несимметричной трехфазной цепи при соединении источника и приемника звездой с нейтральный проводом, сопротивление которого Zn, и пренебрегая сопротивлением линейных проводов и фаз источников.

Напряжение между нейтральными точками n и N (UnN) согласно методу двух узлов равно

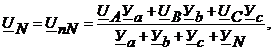(4.11)

где 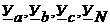– комплексы полных проводимостей соответствующих ветвей.

Напряжения на фазах приемника

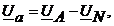
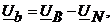
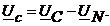(4.12)

Зная фазные напряжения приемника, можно определить фазные токи:

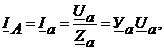
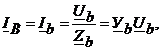(4.13)

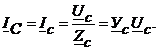
Ток в нейтральном проводе

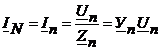
Рассмотренный порядок расчета пригоден и для случая отсутствия нулевого провода.

На рис 4.6 показана векторная диаграмма напряжений для данной цепи.

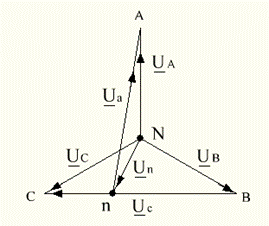
Рисунок 4.6 – Векторная диаграмма напряжений

При наличии сопротивления в нулевом проводе () нейтральная точка приемника на топографической диаграмме не совпадает с нейтральной точкой приемника, поэтому напряжение Un называют напряжением смещения нейтрали. Вследствии смещения нейтрали напряжения на фазах приемника оказываются неодинаковыми, несмотря на симметрию фазных напряжений источника.

В случае соединения несимметричной нагрузки треугольником фазные токи распределяются как

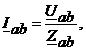
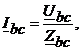
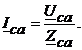(4.14)

Важной особенностью соединения фаз треугольником является то, что при изменении сопротивления одной из фаз режим работы других фаз остается неизменным, т. к. линейные напряжения генератора являются постоянными (буде изменяться только ток данной фазы и линейные токи в проводах линии, соединенных с этой фазой).

Исследование трехфазной цепи при соединении приемников энергии звездой и треугольником проводится бригадами в соответствии с вариантами параметров элементов цепи (табл. 4.1).

Таблица 4.1 — Варианты параметров

4.3 Порядок выполнения работы и методические указания по ее выполнению

4.3.1 Экспериментальные исследования

Собрать электрическую цепь, схема которой представлена на рис 4.7 с параметрами элементов, указанных в таблице 4.1.

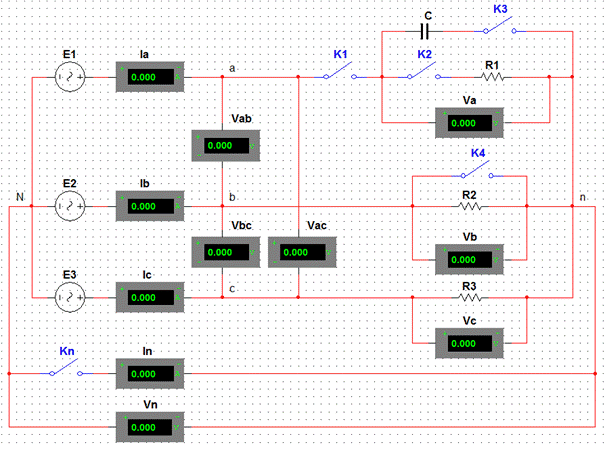
Рисунок 4.7 –Экспериментальная схема для исследования трехфазной цепи при соединении приемников энергии звездой

После проверки преподавателем исследования проводить в порядке, указанном в табл. 4.2.

Таблица 4.2 – Экспериментальные данные измерения напряжений и токов

Собрать схему рис 4.8 (соединение приемника треугольником) и после проверки преподавателем исследования проводить в порядке, указанном в таблице 4.3

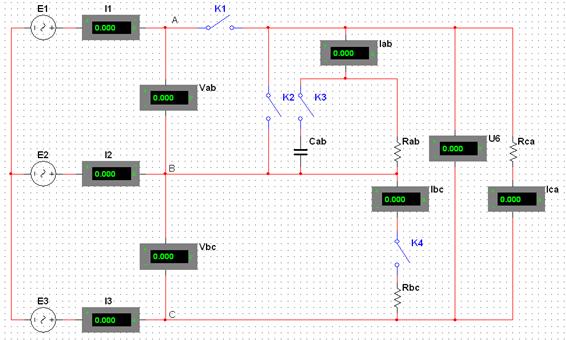
Рис. 4.8 – Экспериментальная схема для исследования трехфазной цепи при соединении приемников энергии треугольником

Таблица 4.3 — Экспериментальные данные измерения напряжений и токов

4.3.2 По результатам таблицы 4.2 и 4.3 для случаев, указанных преподавателем, построить векторные диаграммы напряжений и токов.

4.3.3 Для случая соединения приемников звездой, зная параметры нагрузки и значения линейных напряжений, для случая 3 (табл. 4.2) рассчитать ток нулевого провода и линейные токи.

4.3.4 Для случая соединения приемника треугольником, зная параметры нагрузки и значения фазных токов, для случая 2 (табл. 4.3) рассчитать линейные токи.

4.4 Содержание отчета

Отчет должен содержать:

– название работы;

– цель работы;

– данные варианта задания;

– схемы электрические принципиальные исследуемых цепей;

– векторные диаграммы;

– результаты расчетов;

– выводы.

4.5 Контрольные вопросы и задания

1. Сформулируйте условия симметрии трехфазной цепи.

2. Сформулируйте условия симметрии трехфазной системы напряжений (токов) приемника.

3. Как изменится активная мощность симметричного трехфазного приемника, если приемник переключить с треугольника на звезду?

4. В симметричной трехфазной цепи при соединении звездой без нейтрального провода, линейные токи по 10 А. Чему равны линейные токи при коротком замыкании и обрыве первой фазы?

5. В симметричной трехфазной цепи при соединении треугольником, линейные токи одинаковы и равны 17,3 А. Чему равны линейные токи в случае обрыва первой фазы и в случае обрыва первого линейного провода?

6. Как определить порядок следования фаз в трехфазной цепи?

7. Почему в нейтральном проводе не ставят предохранитель?

8. В каком случае фазное напряжение приемника, соединенного звездой, может превысить фазное напряжение генератора?

5 ИССЛЕДОВАНИЕ ПЕРЕХОДНОГО ПРОЦЕССА ПРИ ВКЛЮЧЕНИИ RC – И RLC – ЦЕПЕЙ НА ПОСТОЯННОЕ НАПРЯЖЕНИЕ

5.1 Цель работы

Целью работы является теоретическое и экспериментальное исследование переходных процессов при подключении электрических цепей первого и второго порядка к источнику постоянного напряжения. Сравнение результатов теоретического и экспериментального исследования.

5.2 Методические указания по организации самостоятельной работы студентов

При подготовке к лабораторной работе необходимо проработать теоретический материал из раздела «Переходные процессы в линейных электрических цепях». Ознакомиться с содержанием лабораторной работы и подготовить бланк отчета.

В работе исследуется переходный процесс при подключении цепи первого порядка (последовательная – цепь) к источнику постоянного напряжения (рис. 5.1).

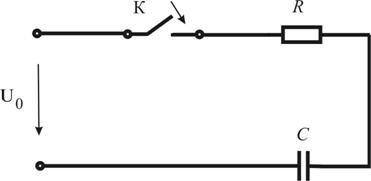
Рисунок 5.1 – Подключение – цепи к источнику постоянного питания

Переходный процесс в такой цепи после коммутации описывается дифференциальным уравнением первого порядка по второму закону Кирхгофа

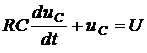. (5.1)

Переходный процесс в последовательной – цепи зависит от параметров элементов цепи, которые определяют постоянную времени данной цепи

. (5.2)

Напряжение на конденсаторе в переходном режиме определяется как:

, (5.3)

а ток в цепи

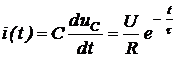. (5.4)

В момент коммутации ток изменяется скачком от 0 до , а напряжение увеличивается от 0 до постепенно.

Таким образом, переходный процесс в – цепи имеет апериодический характер.

В работе исследуется переходный процесс при подключении цепи второго порядка (последовательная – цепь) к источнику постоянного напряжения (рис. 5.2).

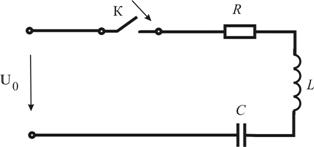
Рисунок 5.2 – Подключение – цепи к источнику

постоянного напряжения

Переходный процесс в такой цепи после коммутации описывается

уравнением, составленым по второму закону Кирхгофа

,

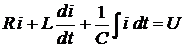откуда получаем дифференциальное уравнение второго порядка

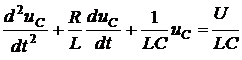. (5.5)

Для решения (5.5) составим характеристическое уравнение, корни которого и определяются как

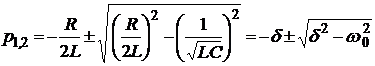, (5.6)

где характеризует затухание колебаний в последовательной – цепи

, (5.7)

а – собственно резонансная угловая частота незатухающих колебаний в этой цепи

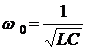. (5.8)

В зависимости от вида корней и различают три различных режима переходного процесса в – цепи: апериодический, критический или предельно апериодический и колебательный. Предел перехода от апериодического процесса к колебательному (критический или предельно апериодический режим) определяется величиной активного сопротивления цепи, когда корни (5.6) одинаковы

,

откуда величина критического сопротивления данной цепи определяется

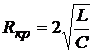. (5.9)

Если активное сопротивление , то в цепи возникает апериодический переходный процесс. Напряжение на конденсаторе в переходном режиме определяется следующим образом

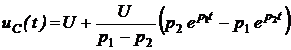, (5.10)

а ток в цепи

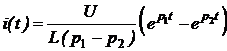. (5.11)

При активном сопротивлении у цепи возникает колебательный переходный процесс. В этом случае корни и будут комплексно сопряженные

,

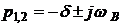где – угловая частота свободных колебаний в цепи, которая определяется как

. (5.12)

Напряжение на конденсаторе при колебательном переходном режиме в – цепи определяется как

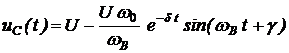, (5.13)

где 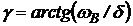, (5.14)

а ток в цепи определяется как

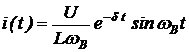. (5.15)

Исследование электрических цепей (см. рис. 5.1, 5.2) проводится бригадами по вариантам. Варианты параметров элементов и параметров входного сигнала приведены в табл. 5.1.

Для исследования переходного процесса с помощью осциллографа необходимо в качестве источника напряжения использовать генератор прямоугольных импульсов, равноценно многократному подключению и отключению изучаемой цепи. Это в свою очередь нужно для исследования переходного процесса с помощью осциллографа. В работе напряжение импульсов изменяется от 0 до 10В, а частота составляет 50Гц. Соответственно длительность периода импульсного напряжения составляет 20мс, а длительность положительного или отрицательного импульса – 10мс.

Таблица 5.1 – Варианты заданий

5.3 Порядок выполнения работы и методические указания относительно ее выполнения

Лабораторная работа включает: экспериментальные исследования (рис. 5.4, 5.7), обработку результатов эксперимента, теоретические расчеты значений функций 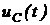, для заданного по варианту момента времени переходного процесса, сравнительный анализ экспериментальных и теоретических результатов.

5.3.1 Экспериментальные исследования

Задачей эксперимента является регистрация осциллограмм входного напряжения, переходных функций тока в цепи и напряжения на конденсаторе 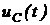при различных переходных режимах в цепи первого и второго порядка. Эксперимент проводится трижды, соответственно регистрируются осциллограммы , , 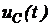, при исследовании переходного процесса в – цепи и исследованиях переходных процессов в – цепи в апериодическом и колебательном режимах. 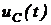Осциллограммы , и , должны быть совмещены во времени. На всех рисунках нужно указать те значения величин, которые были использованы в опыте.

5.3.1.1 Исследования переходного процесса в – цепи

Собрать цепь, схема которой приведена на рис. 5.4. Установить значение R и C, а также параметры источника напряжения.

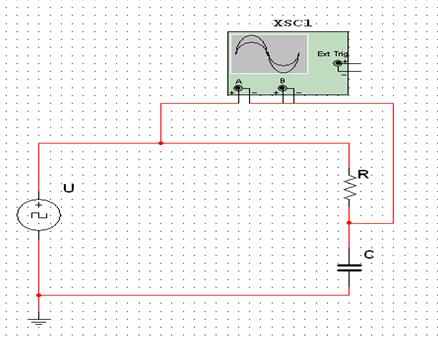
Рисунок 5.4 – Исследование переходного процесса в – цепи

для построения графика

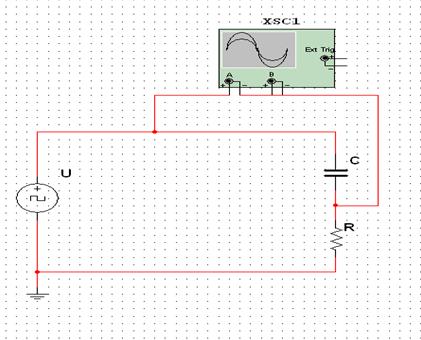
Рисунок 5.5 – Исследование переходного процесса в – цепи

для построения графика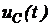

Для регистрации переходных функции и 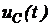в исследуемой цепи установить такие параметры развертки на осциллографе: по оси Х – 1 мс/клет., по оси Y – 5 В/клет. Включить цепь и зарисовать осциллограмму одного импульса входного напряжения и .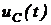

Изменить схему, как это показано на рис. 5.5, включить цепь и зарисовать осциллограмму одного импульса входного напряжения и .

Учитывая, что на резистивном элементе ток и напряжение имеют одинаковую форму и совпадают по фазе, полученная осциллограмма является фактической осциллограммой тока в цепи в соответствующем масштабе.

5.3.1.2 Исследования переходного процесса в – цепи. Построить цепь, схема которого приведена на рис. 5.6. Установить значение R, C и L, а также параметры источника напряжения.

Для исследования апериодического переходного процесса изменить величину 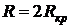, де рассчитать за (5.9).

Подключить первый канал осциллографа к входному напряжению, а второй – к конденсатору и отразить осциллограммы и .

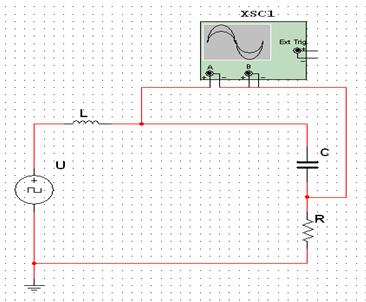
Рисунок 5.6 – Схема исследования переходного процесса в – цепи
для построения графика

Изменить схему согласно рис. 5.7. Включить цепь и отобразить осциллограмму одного импульса входного напряжения и . Обратить внимание на различие полученных осциллограмм и аналогичных осциллограмм при исследовании – цепи.

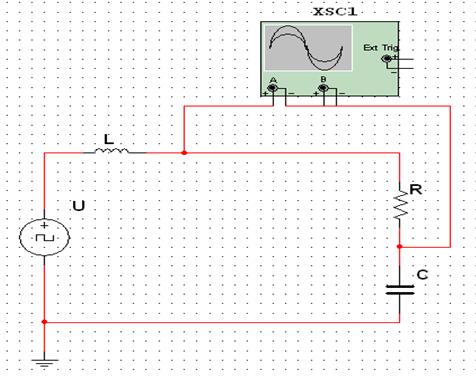
Рисунок 5.7 – Схема исследования переходного процесса в – цепи

для построения графика

Снова вернуться к схеме (рис. 5.6) и наблюдать изменение характера переходного процесса от апериодического к колебательному, постепенно уменьшая величину до 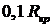. При достижении величины 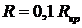зарисовать осциллограммы и , отобразить осциллограмму .

5.3.2 Обработка результатов эксперимента

На каждом из рисунков указать момент времени от начала переходного процесса, заданный по варианту (5.1). Определить на всех осциллограммах значение ,, и записать их в графу «Опыт» табл.5.2. Величину тока по осциллограмме определить, учитывая, что максимальный ток определяется как .

5.3.3 Теоретические расчеты значений переходных функций

Теоретические расчеты значений функций , , проводятся для того же значения , что и в п. 5.3.2. Привести развернутую запись расчетов по формулам (5.3-5.15), а окончательные результаты занести в графу «Теоретический расчет» табл. 5.2.

Таблица 5.2 – Результаты расчетов

5.3.4 Сравнительный анализ результатов

Сравнить результаты графического и аналитического определения значений функций 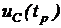, для всех опытов. Сделать выводы.

5.4 Содержание отчета

Отчет должен содержать:

– название работы;

– цель работы;

– данные варианта задания;

– схемы электрические принципиальные исследуемых цепей;

– осциллограммы;

– результаты расчетов (табл. 5.2);

– выводы.

5.5 Контрольные вопросы и задания

1 В каком случае в электрической цепи возникает переходный процесс?

2 Сформулируйте законы коммутации.

3 Что такое постоянная времени переходного процесса?

4 В чем отличия переходного процесса в цепях первого и второго порядка?

5 При каких условиях возможен колебательный переходный процесс?

6 Какой порядок анализа переходных процессов классическим методом?

7 Как проявляются переходные процессы в электронной технике?