Элементарные релятивистские задачи
Задача 6. Из выражения полной энергии (5) с очевидностью следует, что при уменьшении скорости частицы до нуля импульс уменьшается также до нуля, а энергия — до энергии покоя. Попытайтесь получить этот факт из преобразований Лоренца. Для этого движение частицы примите за движения новой системы отсчета и учтите, что скорость частицы можно выразить через импульс и полную энергию.
Решение. Итак, в уравнении преобразования энергии v — скорость частицы. В соответствии с определениями 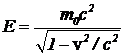 , и px=p=
, и px=p=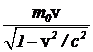 , (pY= pZ=0) имеем
, (pY= pZ=0) имеем 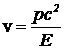 . (12) Определим теперь энергию частицы в системе отсчета, в которой частица покоится, используя формулу преобразования энергии (11),
. (12) Определим теперь энергию частицы в системе отсчета, в которой частица покоится, используя формулу преобразования энергии (11), 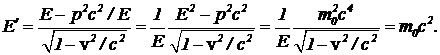 (13)
(13)
В цепочке уравнений (13) учтено, что 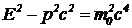 , и использовано выражение полной энергии частицы через ее скорость.
, и использовано выражение полной энергии частицы через ее скорость.
4. Домашнее задание
4.1 Теоретический материал
Проработать материал по пособию и своим конспектам. Дополнительно по учебнику “Физика 11” под ред. А. А.Пинского. §54.
4.2 Решение задач
Задача 1. При какой скорости кинетическая энергия релятивистской частицы будет равна ![]() ?
?
Задача 2. При какой кинетической энергии заряженный пион с собственным временем жизни 2,5 10-8 с пролетит до распада 100 м? Энергия покоящегося пиона равна примерно 140 МэВ.
Указание: используйте формулы для релятивистской энергии частицы и (12).
Задача 3. Квант электромагнитного излучения является элементарной частицей — фотоном — с инвариантной массой, равной нулю. Каково соотношение между энергией и импульсом фотона? С какой скоростью должен двигаться фотон? Что бы с ним было, если бы его удалось остановить?
занятие 1.6.3
элементарные релятивистские задачи
2. Инертная и гравитационная масса
2.1 Инертность энергии
В природе есть три очень похожие друг на друга частицы — положительно, отрицательно заряженные и нейтральный пионы. Единственным отличием частиц является их заряд. Массы заряженных пионов абсолютно одинаковы, а нейтральный пион немного легче. Небольшое отличие масс объясняет теория относительности. Заряженные пионы создают вокруг себя электрическое поле. Поле обладает энергией (плотность энергии электрического поля равна ![]()
![]() , E— напряженность электрического поля). В соответствии с законом E=mc2 электрическое поле, создаваемое заряженными пионами, обладает массой. Таким образом, разница масс заряженных и нейтрального пиона равна массе электрического поля.
, E— напряженность электрического поля). В соответствии с законом E=mc2 электрическое поле, создаваемое заряженными пионами, обладает массой. Таким образом, разница масс заряженных и нейтрального пиона равна массе электрического поля.
Задача 1. Электрон как заряженная частица создает вокруг себя электрическое поле. Электрическое поле обладает положительной потенциальной энергией, с которой должна быть связана масса. Какой радиус должен иметь электрон, чтобы вся его масса была массой электрического поля? Считайте, что электрический заряд электрона распределен по поверхности сферы. Заряд электрона равен 1.6×10-19 Кл, масса электрона – 9.1×10-31 кг.
2.2 На релятивистскую добавку к массе действует поле тяготения
Релятивистская масса различна в разных системах отсчета. В некоторой системе отсчета масса частицы может во много раз превышать массу покоя, в то время как в системе отсчета, связанной с частицей, ее масса равна массе покоя. Встает вопрос о реальности релятивистской добавки массы? Есть ли опыты, в которых проявляется релятивистская масса? Релятивистская добавка проявляется экспериментально. Фотоны — это частицы с нулевой массой покоя. Вся их масса состоит из релятивистской добавки. На фотоны, как и на другие материальные тела, действует поле тяготения. Пролетая мимо звезды, под действием гравитационного притяжения к звезде фотон отклоняется.
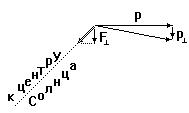
Вопрос 1. Во время полного затмения Солнца на небосводе видны звезды. В окрестности Солнца их расположение чуть-чуть изменяется. Небосвод вокруг Солнца как бы растягивается. Звезды, видимое положение которых близко к Солнцу, слегка “отталкиваются” от Солнца. Объясните этот эффект.
Задача 2. Рассчитать максимальное значение углового смещения изображения звезды, обусловленного гравитационным отклонением излученного звездой света. Масса Солнца M=2×1030 кг, радиус Солнца R»0.7 млн. км.
|
|
Решение. Отклонение светового луча возникает вследствие приобретения поперечного импульса p^. Он равен полному импульсу поперечной составляющей силы притяжения фотона к Солнцу — F^. Учтем следующие обстоятельства, сопровождающие распространение фотона: скорость фотона равна скорости света и не зависит от действующих на него сил; угол отклонения J мал – J<<1. Это означает, что при прохождении фотона мимо Солнца изменяется только направление импульса, но не его модуль p и p>>p^. По определению, приобретенная за бесконечно малое время dt поперечная составляющая импульса равна
![]() , (1)
, (1)
где dx — бесконечно малое перемещение фотона за время dt. Полный импульс поперечной составляющей силы притяжения F^ равен сумме по всем малым перемещениям —
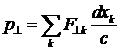 . (2)
. (2)
Пусть R — расстояние от траектории фотона до центра Солнца. Построим цилиндр радиуса R с осью, параллельной направлению распространения фотона. Если умножим обе части уравнения (2) на 2pR
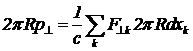 , (3)
, (3)
то можно заметить, что множитель 2pRSF^dx в правой части получившегося уравнения равен потоку вектора силы притяжения фотона к Солнцу.
Если mg — масса фотона, то сила притяжения его к Солнцу равна
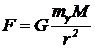 , (4)
, (4)
где M — масса Солнца. Как видно, имеет место кулоновская зависимость. Если по аналогии с электростатикой ввести поток вектора силы гравитационного притяжения, то можно получить аналог закону Гаусса: поток вектора силы через произвольную замкнутую поверхность, охватывающую источник поля, равен потоку через сферическую поверхность. Так как построенный нами цилиндр имеет бесконечную длину, поток вектора силы через боковую поверхность равен потоку через замкнутую поверхность или, по теореме Гаусса, равен 4pGmgM. Таким образом, уравнение (3) принимает вид 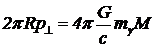 , (5)
, (5)
которое дает 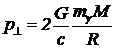 . (6)
. (6)
Как было установлено на прошлом занятии, полный импульс равен 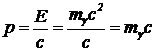 . (7)
. (7)
С учетом малости отклонения искомый угол оказывается равным J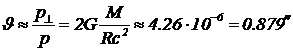 (8)
(8)
Получилось немногим меньше одной угловой секунды. Такое, пусть малое отклонение, современными средствами измерения надежно обнаруживается. Данные измерений и расчеты согласуются между собой. [Строгий расчет по общей теории относительности, учитывающий изменение пространства и времени вблизи Солнца, дает результат в два раза больший.]
Вывод: вся масса фотона, являющаяся релятивистской, испытывает действие силы тяготения.
Интересно рассмотреть еще один экспериментальный факт, подтверждающий действие силы тяготения на фотоны. Можно измерять энергию фотонов в поле тяжести Земли, и убедиться, что при изменении его положения по высоте на h потенциальная энергия изменяется на mggh. Эта возможность появилась после открытия Мёссбауэром способа получения пучков фотонов со строго определенной частотой w. Чтобы разобраться в явлении, надо ознакомиться с одним из результатов квантовой физики. Известно, что фотоны одновременно являются и частицами, и электромагнитной волной. (Эта особенность сущности фотонов будет изучаться немного позднее.) Энергия фотона-частицы E связана с частотой электромагнитной волны соотношением 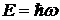 , где
, где ![]() – постоянная Планка, равная 1.05×10-34 Дж×с. Энергию можно считать кинетической. Если выпустить фотоны снизу вверх, то по мере их подъема у них увеличивается потенциальная энергия. А так как полная энергия должна оставаться постоянной, то рост потенциальной происходит за счет убыли кинетической энергии. Это выражается в том, что с высотой уменьшается частота фотонов. С помощью эффекта Мёссбауэра удается измерить уменьшение частоты.
– постоянная Планка, равная 1.05×10-34 Дж×с. Энергию можно считать кинетической. Если выпустить фотоны снизу вверх, то по мере их подъема у них увеличивается потенциальная энергия. А так как полная энергия должна оставаться постоянной, то рост потенциальной происходит за счет убыли кинетической энергии. Это выражается в том, что с высотой уменьшается частота фотонов. С помощью эффекта Мёссбауэра удается измерить уменьшение частоты.