Энергия магнитного поля и расчет индуктивности проводников

5.  Два металлических диска радиусом , расположенные друг против друга на расстоянии один от другого, вращаются в противоположных направлениях с угловой скоростью в однородном магнитном поле, вектор индукции которого перпендикулярен плоскостям дисков. Найдите заряд полученного таким образом конденсатора и силу притяжения дисков.

Практическое занятие №8

Энергия магнитного поля и расчет индуктивности проводников

Краткие теоретические сведения

Учитывая симметричность понятий электрического и магнитного поля, выражение для энергии последнего принимает вид

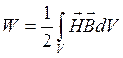. (8.1)

Осуществляя переход от энергии магнитного поля к энергии проводника с током, получим выражение

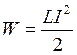, (8.2)

где – индуктивность (коэффициент самоиндукции) проводника.

Рассматривая два контура с током рассчитаем поток вектора магнитной индукции через поверхность первого из них. Получим следующее выражение –

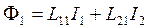, (8.3)

где и – токи в первом и втором контуре, – коэффициент взаимной индукции, – коэффициент самоиндукции первого контура.

Исходя из определения потока и понятия векторного потенциала, для коэффициента индукции получим общее выражение

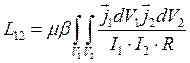. (8.4)

Соответственно для коэффициента самоиндукции –

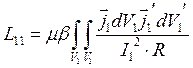. (8.5)

В случае рассмотрения линейных проводников удобно осуществить формальный переход

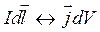. (8.6)

Коэффициенты индукции и самоиндукции зависят лишь от формы контуров их взаимного расположения, и не зависят от токов, которые по ним протекают.

В дальнейшем, говоря об индуктивности проводника, мы будем иметь в виду коэффициент самоиндукции. В остальных случаях удобно использовать термин «коэффициент индукции».

Темы для развернутых ответов

1.  Энергия магнитного поля и проводника с током.

2.  Индуктивность проводника.

Литература: [1], глава 8, §47; [3], глава 4, §52.

Основной блок задач

1.  Рассчитайте энергию и индуктивность соленоида, имеющего витков, длину , сердечник с магнитной проницаемостью . По соленоиду течет ток , а площадь сечения витка .

2.  Линия состоит из двух коаксиальных тонких цилиндрических оболочек с радиусами и (), пространство между ними заполнено веществом с магнитной проницаемостью . Найдите индуктивность единицы длины данной линии.

3.  Определите индуктивность единицы длины двухпроводной линии. Линия состоит из двух параллельных прямых проводов, радиусы которых и , расстояние между осевыми линиями . По проводам текут равные по величине, но противоположные по направлению токи .

Дополнительный блок задач

4.  Определите индуктивность тонкого проволочного кольца радиуса . Радиус провода .

5.  Найдите индуктивность единицы длины бесконечного цилиндрического соленоида с густой намоткой и с произвольной формой сечения. Площадь сечения , число витков на единицу длины .

6.  Длинный прямой провод и кольцо радиуса лежат в одной плоскости. Расстояние от центра кольца до провода . Найдите коэффициент взаимной индукции , если сила тока в проводниках равна соответственно и .

Практическое занятие №9

Законы Ома и Джоуля-Ленца

Краткие теоретические сведения

На основе экспериментально открытого Г. С. Омом закона, связывающего ток в проводнике с приложенной к нему разностью потенциалов (закон Ома для однородного участка цепи)

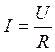(9.1)

запишем его дифференциальную форму для плотности тока. Учтем, что удельное сопротивление проводника связано с его проводимостью как